作者:Ciamac Moallemi、Dan Robinson,Paradigm
編輯:Yangz,Techub News
簡介
在這篇文章中,我們將介紹一種專為預測市場量身定制的新型自動做市商(AMM):pm-AMM。
AMM 及其前身(如市場評分規則)最初是作為一種為預測市場提供流動性的方式而發明的。現在,它們主導著大部分DEX 的交易量。然而,諷刺的是,儘管預測市場的交易量急劇上升,但其中大部分使用的是訂單簿,而非AMM。
其中一個可能的原因是,現有的AMM 並不適合結果代幣(即如果事件發生,代幣的價格為1 美元,而如果事件沒有發生,代幣的價格為0 美元)。結果代幣的波動取決於事件的當前機率和預測市場到期的時間,這意味著資產池提供的流動性是不一致的。一旦預測市場到期,流動性提供者(LP)基本上會失去其所有價值。
為此,我們提出了一種圍繞這些考慮因素進行最佳化的新型AMM,旨在解決AMM 研究中一個長期存在的問題,即針對特定類型的資產優化AMM 意味著什麼?換句話說,給定某種資產(如選擇權、債券、穩定幣或結果代幣)的模型,會如何影響我們應用的AMM?我們根據損失與再平衡(LVR)的概念,提出了這個問題的可能答案。
研究成果
我們為一些結果代幣的價格變動建立了一個模型,我們稱之為高斯分數動態模型(Gaussian score dynamics)。該模型可能適用於預測市場,能夠預測某些基本隨機走勢(如籃球比賽的比分差距、選舉中的票數差距或某些資產的價格)在未來特定到期時間是否會高於某個數值。
我們利用這個模型為這些代幣推導出了一種新的基於不變式的AMM,即靜態pm-AMM 不變性:
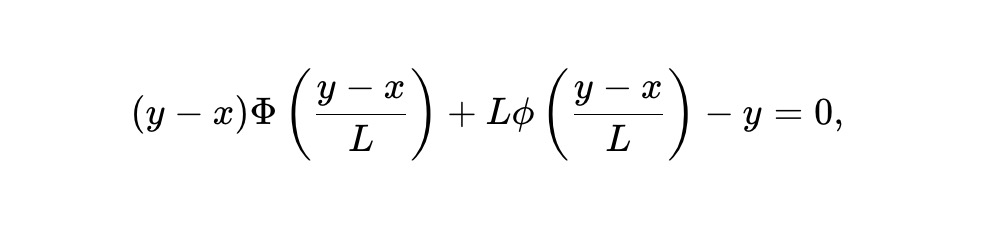
其中,x 是AMM 中結果代幣的儲備,y 是其對立、互補結果代幣的儲備, L 是總體流動性或比例係數,ϕ 和Φ 分別代表常態分佈的機率密度函數和累積分佈函數。
上述不變式是基於一個強大的概念,即損失與再平衡(LVR),我們可將其視為AMM 因套利而虧損的比率,LVR 取決於AMM 的形狀和在AMM 上交易的相關資產的價格變動。
我們將某一資產的統一AMM(uniform AMM)定義為,如果用於該資產,那麼無論當前價格如何,該AMM 的LVR 都與其在某一時刻的投資組合價值成正比。 Milionis 等人認為,對於價格遵循幾何布朗運動(GBM,適用於股票和加密貨幣等普通資產價格變動的流行模型)的資產,恆定幾何平均數做市商(如Uniswap 和Balancer)是唯一的統一AMM ,而靜態pm-AMM 是針對資產行為遵循我們提出的結果代幣高斯分數動態模型的統一AMM。
雖然靜態pm-AMM 在所有價格下都具有統一的LVR(作為投資組合價值的一部分),但隨著預測市場到期日的臨近,LVR 仍會增加。這是因為預測市場在接近到期時可能會非常不穩定。為調整pm-AMM 以降低其流動性,從而使AMM 在到期前的剩餘時間內所有時刻的預期LVR 保持不變,我們推導出了動態pm-AMM 不變性,而它取決於到期時間Tt:
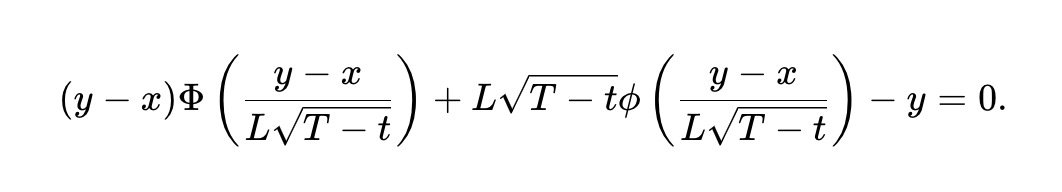
動態pm-AMM 的機制透過提供不斷減少的流動性,防止LVR 隨著到期日的臨近而增加。在真實資金池中,這未必是可取的,尤其是因為非套利交易活動(以及因此產生的費用)也可能隨著時間的推移而增加。但是,pm-AMM 為流動性提供者提供了一個框架,使其可以根據預期費用以及他們希望如何分配套利風險來調整流動性。
這些AMM 可能有助於引導鏈上預測市場的被動流動性。統一AMM 的概念以及相關方法也可能更廣泛地適用於DEX 的設計者,他們可以利用這些方法為價格變動不遵循幾何布朗運動的其他類型資產定制AMM,如穩定幣、債券、期權或其他衍生品。
圖1 顯示了靜態和動態pm-AMM 的不變曲線(invariant curve),並與其他知名的不變曲線,即恆定產品做市商(CPMM) 和對數市場計分規則(LMSR) 進行了比較。請注意,動態pm-AMM 的儲備曲線隨著時間的推移提供的流動性較低。
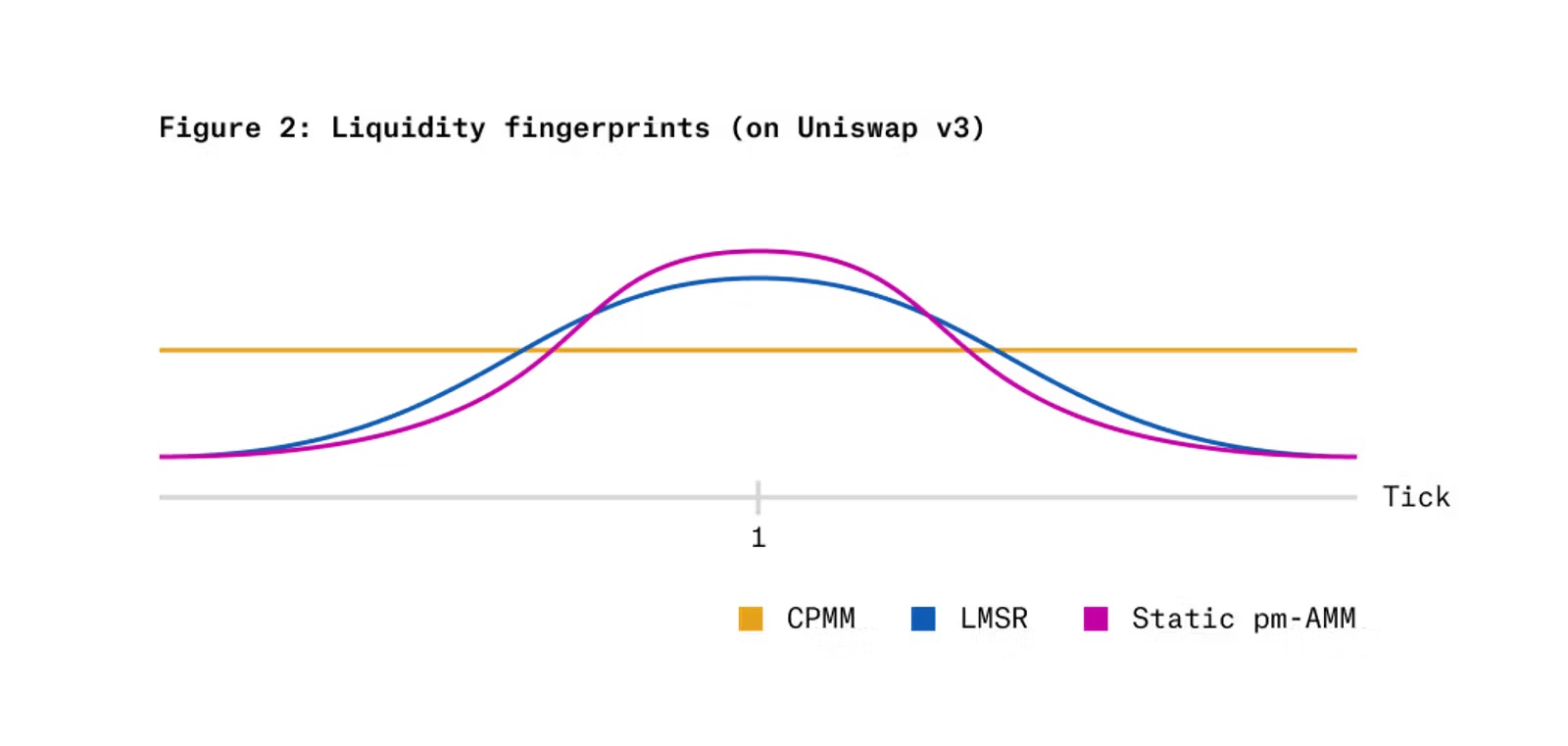
圖2 顯示如果在Uniswap v3 集中流動性AMM 上實施靜態pm-AMM 不變性,與CPMM 和LMSR 相比會出現的「流動性指紋」(liquidity fingerprint )情況。橫軸對應相對價格(x 代幣的價格除以y 代幣的價格)的對數刻度,縱軸對應每個AMM 在該價格水準上的流動性。可以看到,與這兩種替代方案相比,pm-AMM 在相對價格為1(機率為50%,即代幣價格相等於0.50)時集中了更多的流動性,而在極端相對價格(極低或極高)時則集中的流動性較少。
研究背景
預測市場
預測市場是加密貨幣中越來越受歡迎的應用。光是2024 年10 月,Polymarket 的交易量就超過了20 億美元。然而,大多數加密貨幣預測市場的流動性是在訂單簿上提供的,而不是AMM,儘管後者在加密貨幣的大多數DEX 交易量中佔據了主導地位。
其中一個可能的原因是,結果代幣的價格行為與普通資產不同,因此為它們設計的AMM 無法穩定運作。舉個例子,想像一下有關拋硬幣遊戲的預測市場,在該遊戲中,有人會擲1001 次硬幣,而每種結果(正面與反面)分別對應x 和y 兩種代幣。最終,如果正面比反面多,x 代幣的價值為1 美元,而如果反面比正面多,x 代幣的價值為0 美元;y 代幣則反之。
這些結果代幣的波動性很大程度上取決於剩餘的拋擲次數和當前的拋擲情況。當前情況越是相近,剩餘的拋擲次數越少,這些代幣的波動性就越大。這意味著,恆定產品做市商的損失(如下所述取決於波動率)隨時間變化很大。
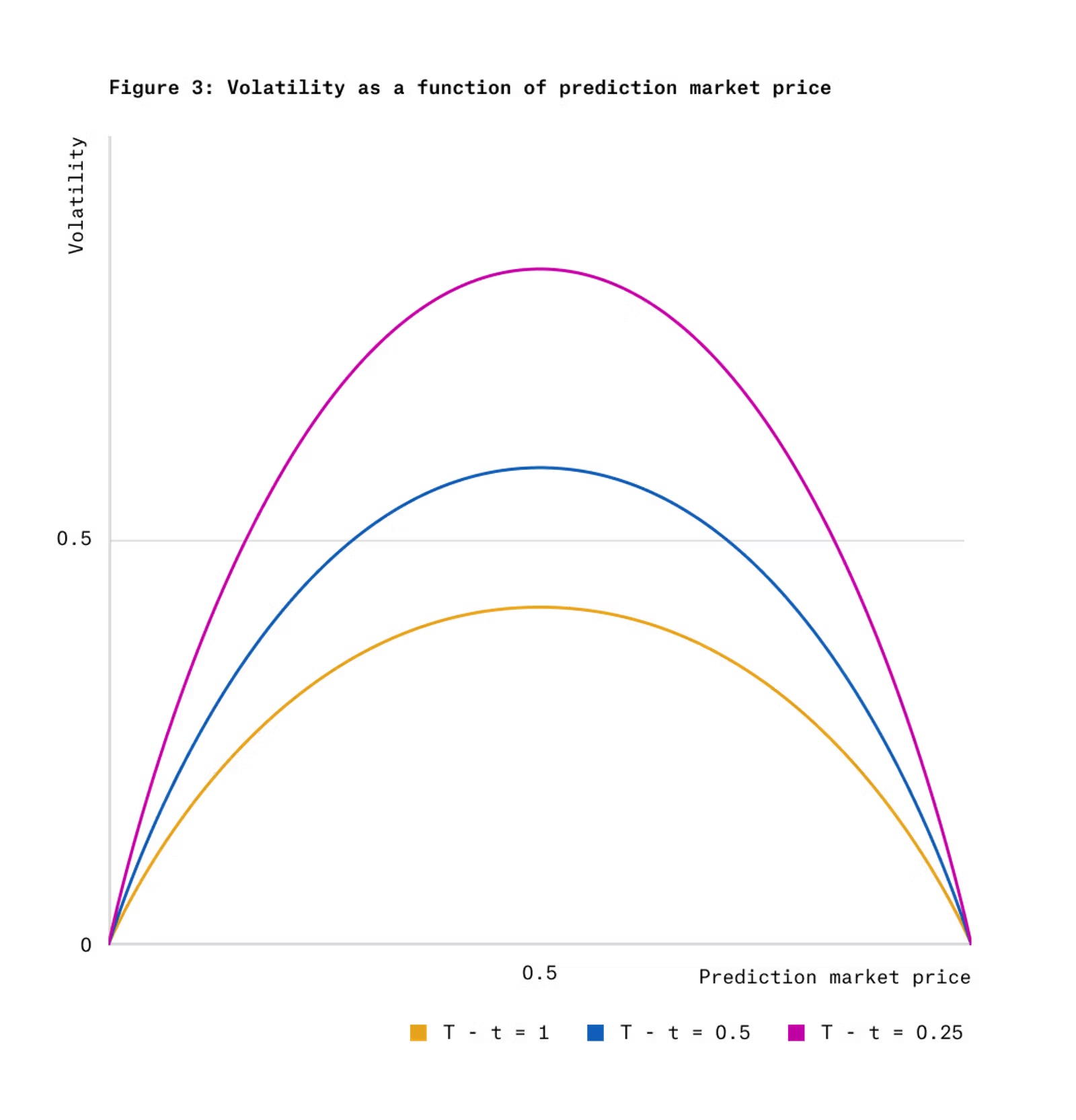
圖3 顯示了在高斯分數動態條件下,結果代幣價格的波動性與代幣價格和剩餘時間的函數關係。
許多流行的預測市場其實與這個拋硬幣的例子類似,賭的是在未來某個到期時間,某種隨機走勢的終點是高於還是低於0。例如:
- 在關於一場籃球比賽結果的預測市場中,一旦比賽剩餘時間為0,市場就會到期。隨機走勢是兩隊之間的得分差異。
- 關於總統選舉結果的預測市場會在選舉日到期。其中,隨機走勢是打算投票給候選人的選民人數之差。
- 關於未來某一日期,比特幣等資產的價格是否高於某個執行價格的預測市場中,隨機走勢可以是當前比特幣價格減去某個行使價的對數。
本文我們定義的結果代幣的價格變動模型,即高斯分數動態模型的靈感就來自這類範例。模型假定,預測市場價格與某些潛在布朗運動結束於0 以上的機率相符。該模型類似於二元期權的Black-Scholes 模型(二元期權是一種工具,如果資產價格高於某個行權價,則支付固定的美元金額;如果資產價格低於某個行權價,則支付0 美元)。然而,在我們的模型中,並不要求潛在過程與可交易資產的價格相對應。
我們確實做了一個簡化假設,即結果代幣的價格與它為1 美元的機率相符。這種假設忽略了市場的重要特徵,包括風險和時間偏好,因此研究這些特徵如何影響這個模型會是未來研究的一個主題。
此外,我們也應該看到,並不是所有的預測市場都適合高斯分數動態模型,因為模型假定新資訊出現的速度是可預測的。例如,籃球比賽可能比足球比賽更適合該模型,因為籃球比賽的得分頻率要高得多,因此比分差距的演變隨著時間的推移也會更加一致。此外,有些類型的預測市場與該模型完全不同,例如預測在某一特定日期之前是否會發生某種一次性的意外事件(如地震)。但話又說回來,該模型可能是為其他動態推導模型的有用起點,並且可以作為為任何模型推導出統一AMM 的方法的演示。
損失vs 再平衡和統一性
在明確了這個模型之後,我們推導出了一種可能比現有的AMM(如恆定產品做市商或LMSR)更適合這些代幣的機制。我們使用的指導性指標是流動性提供者的預期損失率,可表徵為「損失與再平衡」(loss-vs-rebalancing)或LVR。
LVR 捕捉了AMM 的主要逆向選擇成本:在沒有交易的情況下,AMM 的價格是靜態的,而隨著新資訊的出現,價格會變得過時。 LVR 反映了AMM 流動性提供者所承受的成本,因為這些過時的價格會被資訊更靈通的套利者利用,他們會以對AMM 不利的價格進行套利交易。因此,LVR 可視為AMM 為使其價格修正而向套利者支付的費用。
此外,在沒有交易費用的情況下,LVR 也是流動性提供者透過單獨持有與作為池儲備一部分的代幣數量完全相同的空頭頭寸,對其LP 頭寸進行Delta 對沖所產生的損失。 因此,LVR 建立在Black-Scholes 選擇權定價模型的主要見解之上。正如選擇權透過與標的資產進行Delta 對沖來消除市場風險一樣,LVR 在消除市場風險後對AMM 中的LP 頭寸進行估值。也就是說,LVR 隔離了在AMM 中作為流動性提供者的特殊性,而不是簡單地承擔持有與AMM 儲備相同代幣的市場風險。
我們考慮的是簡單的基於不變式的AMM,沒有費用或MEV 回收機制。在這種情況下,AMM 一定會因套利而虧損,沒有任何AMM 不變性可以消除LVR(導致根本不產生交易的不變性除外)。此外,即使「最小化」LVR 也沒有實際意義,因為減少LVR 只意味著減少所提供的流動性。
不過,雖然我們無法消除LVR,但我們可以讓LVR 更統一,這樣損失的資產池價值百分比就不會取決於資產的當前價格。我們稱這項特性為統一性(uniformity)。
想像一個贊助商願意在某個零費用預測市場上提供流動性,以了解市場對結果的預測。該贊助商會賠錢,但它也更願意平均分攤損失,而不是將損失集中在特定時間或特定價格。在這種情況下,資產池的當前投資組合價值可以被視為贊助商的「預算」。在統一的AMM 上,如果贊助商在某個時間投入1 美元的流動性,那麼他們在下個時間點的預期損失與資金池的當前狀態無關。
此外,統一性對追求利潤的流動性提供者也有潛在的意義。即使AMM 能夠從損失與再平衡中獲得部分收益,甚至扭虧為盈(透過非零掉期費,或透過MEV 稅等拍賣機制),它仍然需要一些策略來確定如何在不同價格和不同時間分配流動性。我們可以把零費用池的預期損失看作是衡量該策略在特定時間分配多少流動性的一種方法,這種方法考慮到了資產的價格過程。
我們將特定資產的統一AMM 定義為,無論資產的當前價格如何,其預期LVR 都是資產池當前價值的一個恆定分數的AMM。請注意,AMM 是否具有統一LVR 取決於資產本身的價格過程。如Milionis 等人的附錄B.2 所示,如果資產的價格遵循幾何布朗運動,那麼該資產與數倉之間基本上唯一的統一AMM 就是加權幾何平均數做市商,其不變式為:
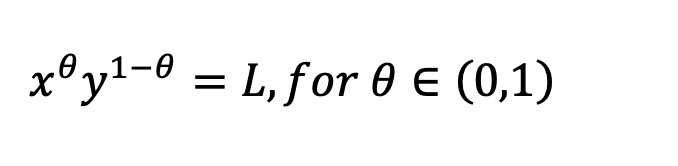
這是Balancer 中使用的公式,Uniswap v2 中使用的常數產品做市商也是其中的一個特例。但對於遵循高斯分數動態的代幣而言,恆定幾何平均值AMM 並不具有統一的LVR。對數市場得分規則(LMSR)也是如此。
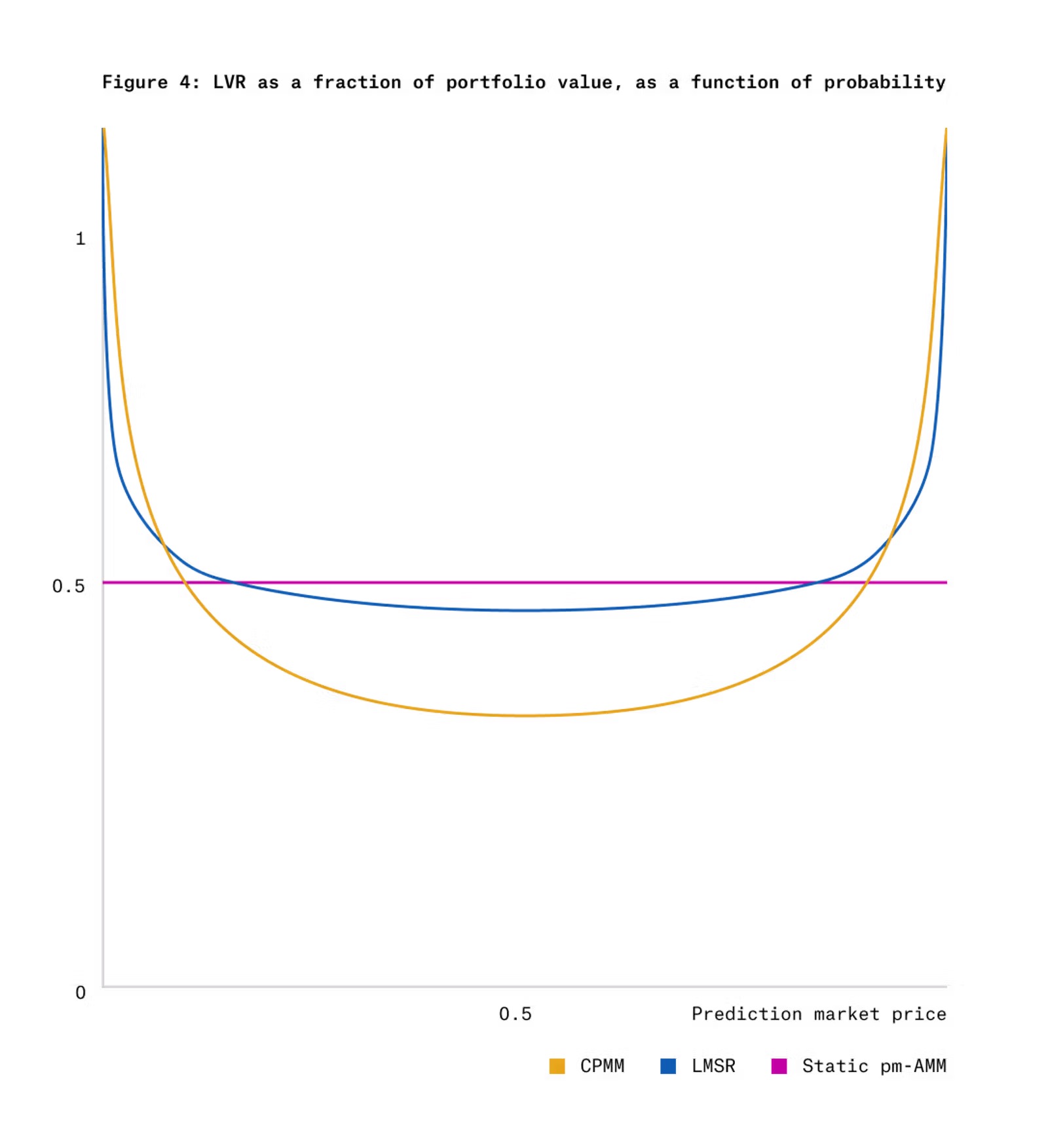
圖4 顯示了CPMM 和LMSR 與靜態pm-AMM 的統一LVR 相比,在時間Tt=1 時用於高斯分數動態結果代幣的LVR。
基於這些考慮,我們開發了兩種針對高斯分數動態條件下為預測市場而設計的AMM:一種是在任何給定時間內具有統一的LVR,但隨著預測市場到期日的臨近,LVR會增加;另一種是在剩餘時間範圍內具有統一的LVR 和恆定的預期LVR。
從圖4 可以看出,當結果代幣價格處於接近零或1 的極端情況時,CPMM 和LMSR 會出現較大的LVR。這是因為,雖然這些點附近的價格波動性較低(參見圖3),但在極端價格下,資產池價值的衰減速度較快。因此,統一的AMM 應該在極端價格時提供較少的流動性,而這正是pm-AMM 設計所做的(參見圖2)。
先前研究
AMM 起源於預測市場和市場評分規則(如LMSR)。這些規則促使人們發現了恆定函數做市商(CFMM),如Uniswap v2,其特徵通常是AMM 對每種資產的儲備之間存在不變關係。基於這種設計的AMM 近年來已成為DEX 的主流市場機制。
近期,金融經濟學的觀點被應用於理解自動做市商的成本,其形式為損失與再平衡(LVR),主要關注幾何布朗運動。另一方面,預測市場的價格動態非常不同,因為它們的收益有限且期限有限。 Taleb 提出了基於潛在的可觀測投票過程的動態,而我們則開發了另一種基於潛在的可觀測高斯分數過程的動態。
在為非GBM 資產設計自動做市商方面,先前已有一些應用研究。其中一個例子是StableSwap,這是一個為穩定幣對設計的AMM,它基於一個直觀的前提,即相關資產和均值回复資產之間的自動做市商應將流動性緊密集中在一個價格上,但它的推導並不涉及對資產價格過程的建模。另一個例子是YieldSpace,這是一個專為零息債券設計的AMM。雖然YieldSpace 的推導確實涉及一個簡單的零息債券定價模型,但它並不包括一個完整的價格過程模型(沒有對利率的演變進行建模)。
此外,學術界也有一些工作是圍繞資產價格行為的信念來設計即時的市場模型。其中一個例子是Goyal 等人的設計。他們的框架是圍繞著最大化預期活躍的流動性而設計的,而不是使預期損失一致,因此有時會得出與我們相反的結果。例如,他們的推導認為,如果流動性提供者預期資產的相對價格會保持在1 左右,那麼LMSR(相對於CPMM,LMSR 將流動性集中在價格1 附近)就非常適合;而我們的框架則認為,如果預期價格會出現分化(如結果代幣),那麼就有理由將流動性集中在1 附近。
各類AMM 模型
自動做市商
我們可以考慮一個有關單一事件的預測市場,以及一個交易兩種競對資產的AMM。其中一種風險資產以x 表示,如果事件發生則支付1 美元,否則不支付任何費用;另一種風險資產用y 表示,支付方式相反。 AMM 保持不變式f(x,y)=L ,其中f(⋅,⋅) 是儲備金(x,y) 的不變函數,L 是常數。給定x 資產的價格P(以美元為單位),則資產池的價值函數為:
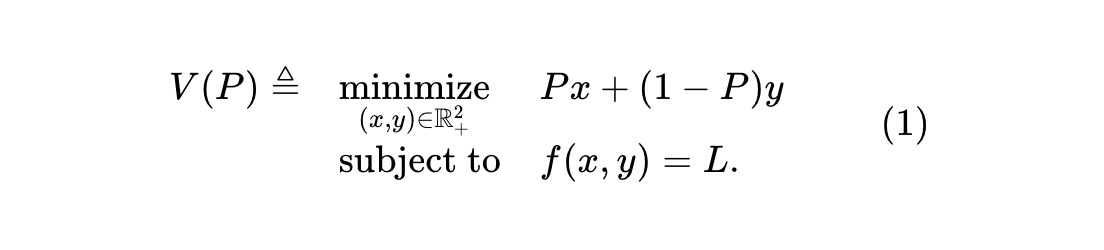
這是當x 價格為P 時的資產池價值。由於分別持有一個單位的x 和y 資產等同於持有現金,我們必須讓y 的價格為1-P。假設有一群套利者,他們在每個時間t 都能觀察到x 資產的價格Pt(以及y 資產的價格1-Pt)。假設沒有交易費用或其他摩擦,這些套利者會持續監控AMM,並試圖從AMM 的任何錯誤定價中獲得價值。在追求自身利潤最大化時,他們會針對AMM 進行交易,使AMM 儲備的價值最小化。如果我們用Vt 表示t 時( 價格為Pt 時)的儲備價值,那麼Vt = V(Pt)。
例1:在恆定產品做市商(CPMM) 的情況下,不變式為f(x,y)≜xy,資產池價值函數為:
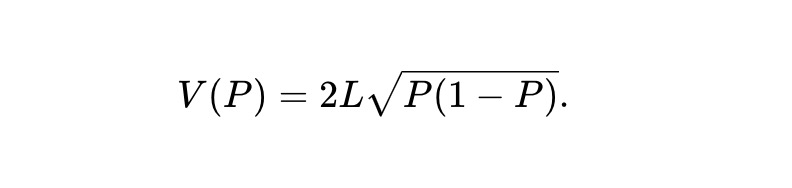
例2:Robin Hanson 所建立的對數市場評分規則(LMSR)可視為符合下列不變式的AMM。
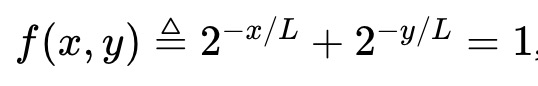
其資產池價值函數為(與價格所隱含事件的二元熵成正比):
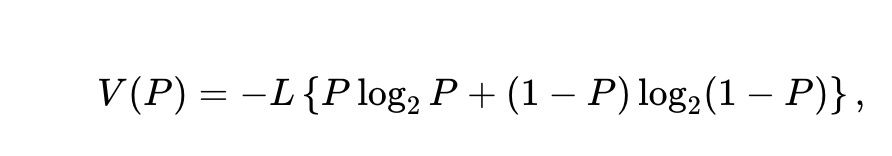
用x ∗(P) 和y∗(P) 表示最佳化問題(1) 的最適解,我們假定它們存在、唯一,且是價格P 的充分平滑函數,那麼下面的公式類似於Milionis 等人的定理1,但適用於當前環境:
定理1. 對於所有價格P≥0,資產池的價值函數滿足:
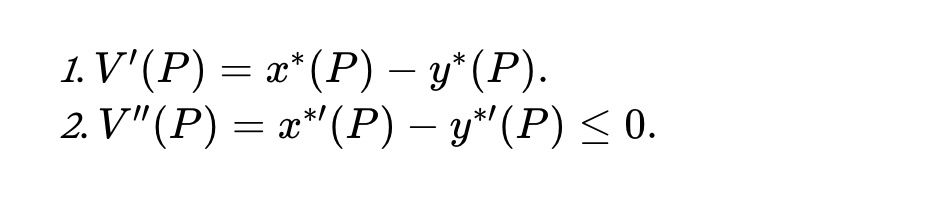
高斯分數動態
風險資產價格如何根據我們所謂的高斯分數動態隨時間演變?具體而言,我們假設在時間區間t∈[0,T] 上存在一個隨機過程{Zt},其中的事件由Zt 在時間跨度t=T 結束時的符號決定:如果ZT≥0,則x 資產償付,如果ZT<0,則y 資產償付。我們可以把Zt 理解為雙邊競爭中兩隊的分差。因此,我們將視Zt 為即得分過程。請注意,雖然我們的模型假定有這個分數過程,但AMM 並不需要直接觀察到這些過程。如下文所述,AMM 可以根據邊際價格(套利後)和到期時間推斷分數的當前值。
我們假設Zt 遵循隨機變動。具體來說,我們假設Zt 是波動率σ>0 的布朗運動,即dZt=σdBt,其中Bt 是標準布朗運動。那麼,不難看出x 資產在時間t 的價格Pt 為:
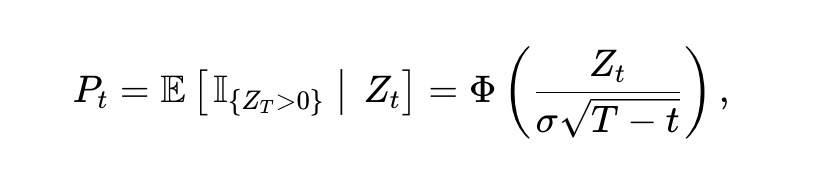
其中,Φ(⋅) 是標準常態累積分佈函數(CDF)。應用伊托(Itô)定理,Pt 必須滿足:
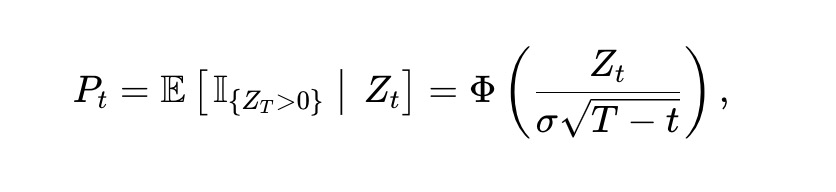
其中,ϕ(⋅) 是標準常態機率密度函數,Φ-1(⋅) 是反CDF。請注意,雖然分數動態和分數到價格的轉換或反向轉換取決於σ,但孤立的價格過程Pt 的動態並不取決於σ。這些動態的波動與價格和剩餘時間的函數關係如圖3。
統一AMM
根據上文的討論,如果我們用Vt 表示資產池儲備在時間t 的價值(此時價格為Pt),則Vt=V(Pt)。應用伊托(Itô)定理,我們可以得到資產池價值是根據以下公式變化的:
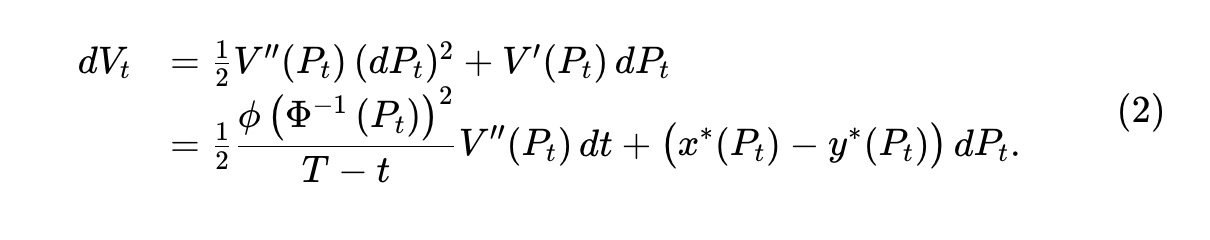
由於價格Pt 是鞅(martingale),那麼(2) 的第二項也是鞅,可能是遞增或遞減的。然而,根據V(⋅) ( 參見定理1),第一項對應的是負轉化,因此是一個遞減過程。這就是Milionis 等人提出的損失與再平衡過程,它捕捉了在不利價格下與資產池進行對沖交易的套利者所損失的價值。我們將這種損失的瞬時速率定義為:
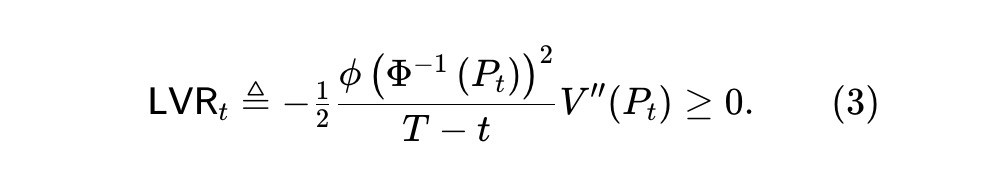
Milionis 等人發現,對於遵循幾何布朗運動的資產,基本上只有幾何均值做市商才是統一AMM。在高斯分數動態下的預測市場中,要檢視(3),統一LVR 池就必須求解以下常微分方程(ODE):
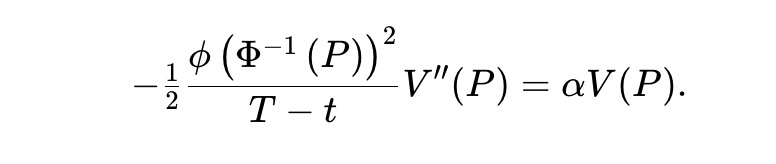
這是不可能的,因為等式左邊取決於t,而右邊不取決於t。這裡的核心問題在於,幾何布朗運動的動態是跨時間不變的,而高斯分數動態則與時間高度相關。
為了規避這個問題,我們允許α 與時間相關,也就是說,我們可以設定α=β/(Tt),其中β>0,那麼就考慮這樣一個設置,即:
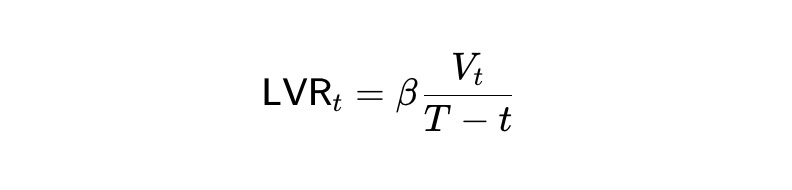
這就等同於P≥0 的ODE。此外,V(⋅) 還有一些額外的要求,例如V′′(P)≤0(參考定理1)。
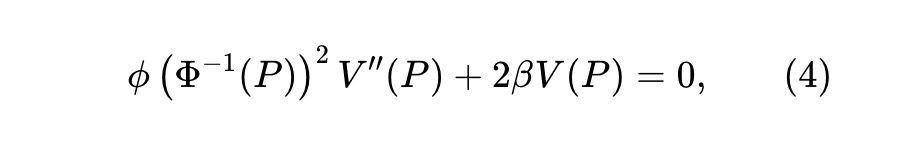
靜態pm-AMM
透過改變變數u=Φ-1(P) 可以簡化上述ODE。當β=1/2 時,有一個既滿足ODE 又滿足額外凹性要求的解,其值為:

x 和y 代幣的儲量為:
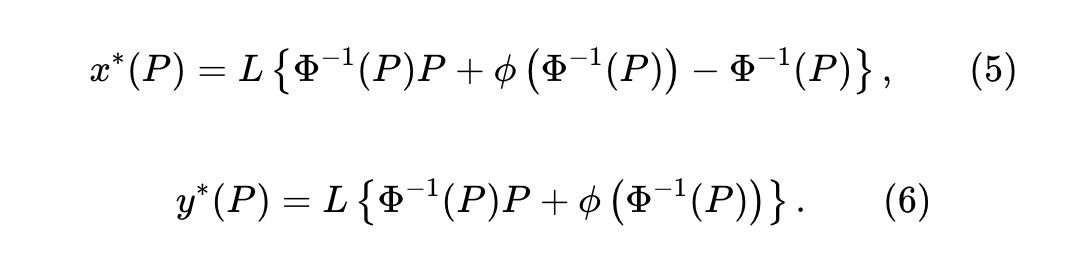
這裡,L≥0 是一個流動性參數,決定了資金池規模的縮放。觀察y∗(P)-x∗(P)=LΦ-1(P),並將其代入(5),則資金池保留(x,y) 必須滿足不變式:
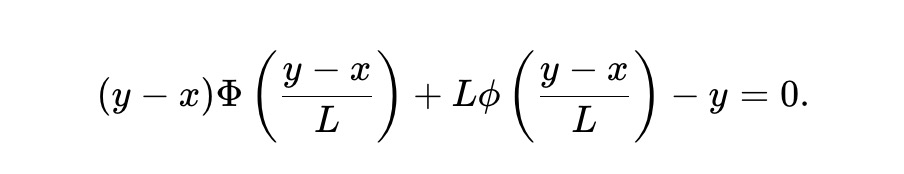
這就是靜態pm-AMM 的定義。根據設計,此AMM 滿足以下關係式:
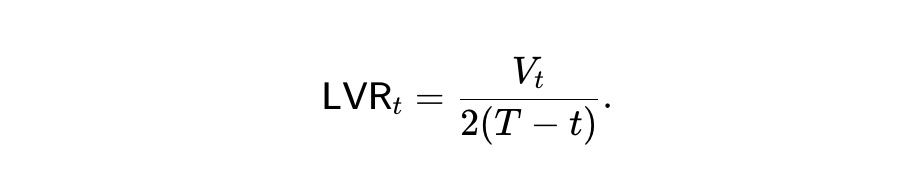
定義Vˉt=E[Vt] 為預期池值,由(2)可得:
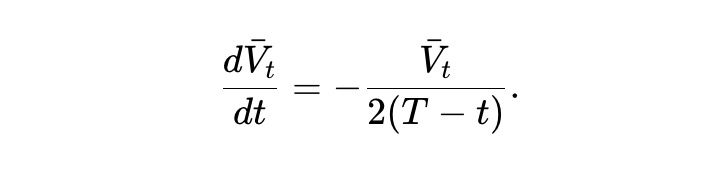
求解此常微分方程,可以得到以下答案。換句話說,在預期情況下,靜態pm-AMM 的資產池價值會根據剩餘時間範圍的平方根衰減。
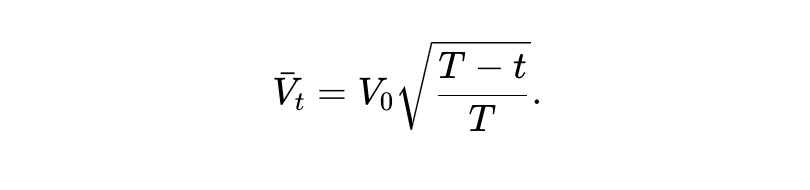
動態pm-AMM
靜態pm-AMM 的一個缺點是,雖然其每美元價值的LVR 在所有可能的價格中都是統一的,但它會隨著時間的推移而變化。特別是,每1 美元價值的損失與到期時間成反比,因此它將隨著時間的推移而增加,直至到期時失去所有價值。
動態流動性。我們設想了一種靜態pm-AMM 設計的動態時變體,即AMM LPs 隨時間提取流動性以減少損失。具體而言,假設資金池價值為:
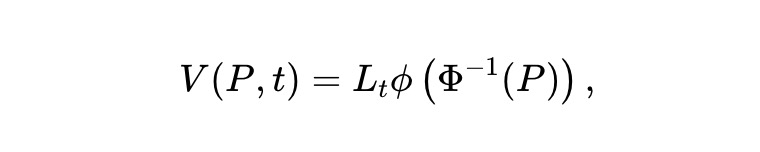
其中,Lt 是一個確定性的平滑函數,它決定了隨著時間的推移,流動性被移除(或可能被增加)的程度。將伊托(Itô)定理應用於資產池價值過程Vt≜V(Pt,t),則
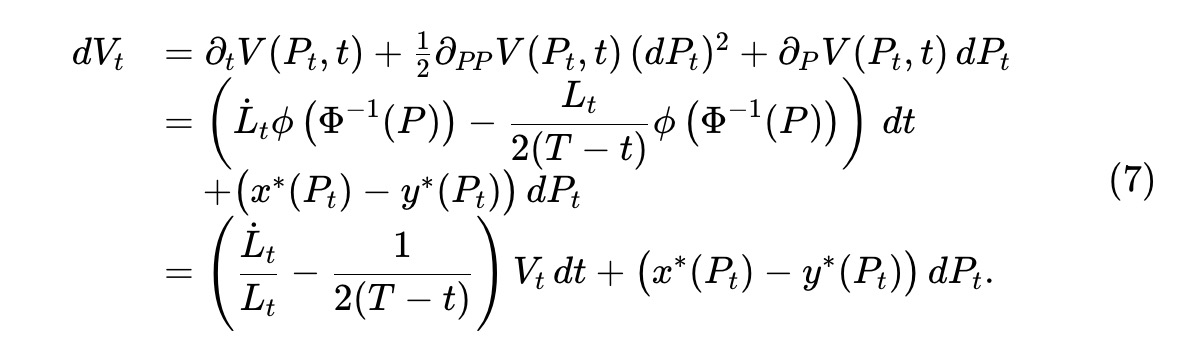
用Ct 表示提取流動性的累積美元價值。由於資金池價值與流動性Lt 呈線性關係,因此Lt 變化的美元價值與Vt/LT 成正比。我們可以得到:
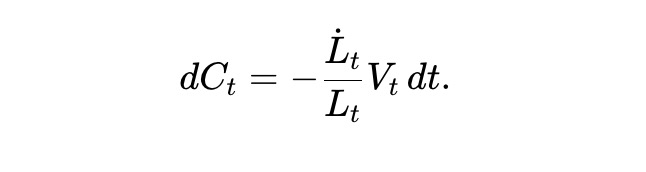
AMM LPs 的總財富Wt 由資金池儲備價值和提取的流動性累積價值組成,因此Wt=Vt+Ct,並滿足:
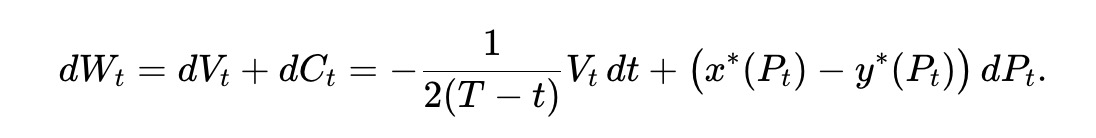
這意味著LP 的預期財富Wˉt≜E[Wt] 滿足以下條件,其中Vˉt≜E[VT]。
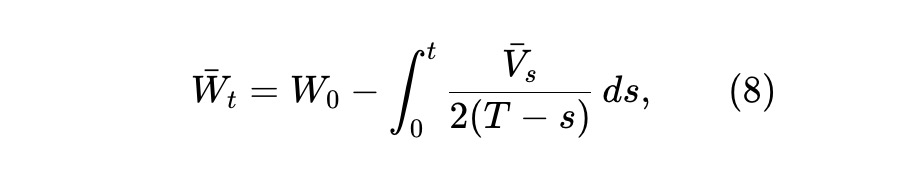
現在,考慮流動性曲線的具體選擇如下:
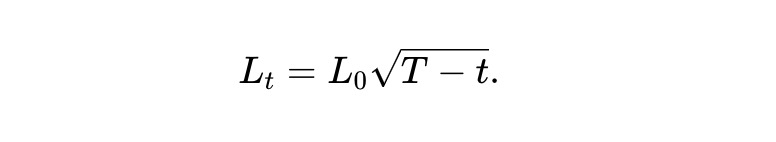
我們稱之為動態pm-AMM。而根據(7),預期資產池價值Vˉt=E[Vt] 滿足:
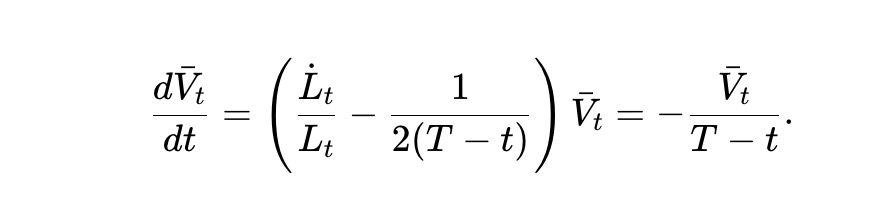
求解此常微分方程,可以得到以下答案。
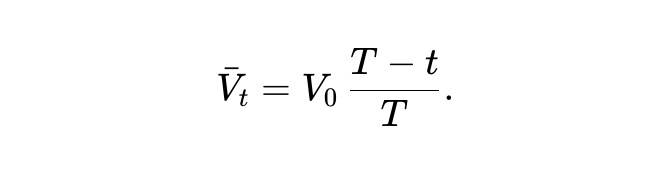
換句話說,在動態pm-AMM 中,扣除提款後,預期資金池價值呈線性下降。此外,由於繼承了靜態pm-AMM 的價值函數,單位時間內的LVR 損失率為:
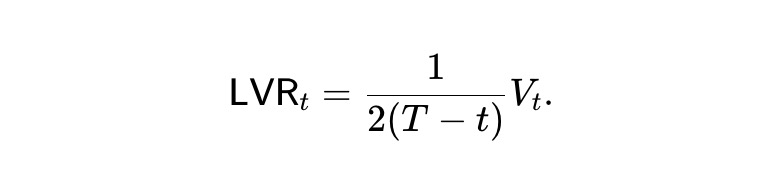
預期損失率為以下值,在t 期間保持不變。也就是說,隨著時間的推移,動態pm-AMM 會以恆定的速度(預期)損失套利者的資金。
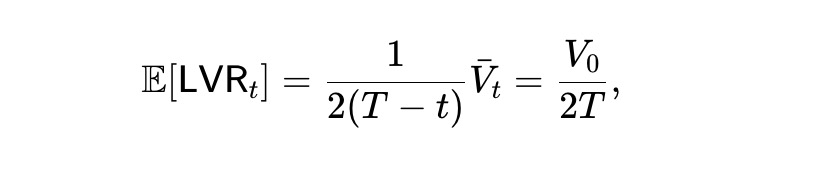
最後,根據(8),得出預期財富過程為下圖所示。因此,初始財富的一半會在最後損失掉。
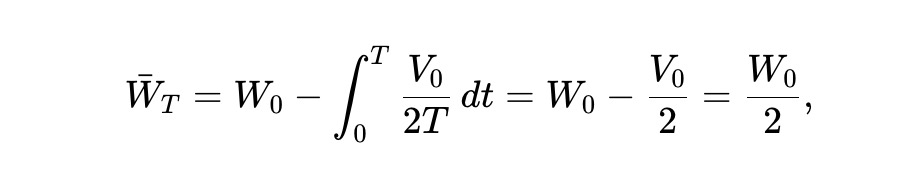
結論
pm-AMM 可能適用於由類似高斯分數動態模型等動態驅動的預測市場。除此之外,我們的研究還表明,統一AMM 可能適用於其他類型的資產,如債券、選擇權和其他衍生性商品。












