PART5.Performance and Risk Management
資金管理-本節討論交易中最基本的概念之一——自由裁量權和算法——即資金管理。天真的投資者/交易員可能認為,唯一重要的投資目標就是盡可能多地賺錢。然而,長期交易的現實更為複雜。由於市場參與者有不同的風險偏好和約束,投資者可能擁有許多目標。
許多散戶認為,唯一的目標是不斷增加賬戶淨值,而很少或根本不考慮實現這種增長的策略的“風險”。更老練的散戶投資者會衡量賬戶的回撤情況,根據他們的風險偏好,他們或許能夠應對賬戶淨值的大幅下降(比如50%)。他們之所以能夠應對如此大規模的回撤,是因為他們認識到,從量化上講,通過使用槓桿,這種行為可能是投資組合長期增長率的最佳選擇。
機構投資者可能會從另一個角度考慮風險。機構投資者通常規定了最大回撤額度(比如20%),並對行業配置和日均成交量限制給予了重要考慮。它們將成為資本配置策略“優化問題”的額外約束。這些因素甚至可能比最大化投資組合的長期增長率更重要。
因此,我們可以在通過槓桿使長期增長率最大化和通過限制回撤的持續時間和幅度使“風險”最小化之間取得平衡。幫助我們實現這一目標的主要工具叫做凱利準則。
凱利準則-在這一部分,凱利標準將是我們的工具,以控制槓桿,並分配到一套算法交易策略,組成一個多策略的投資組合。
我們將把槓桿定義為一個投資組合的規模與該投資組合中實際賬戶淨值的比率。為了更清楚地說明這一點,我們可以用抵押貸款買房來做類比。你的首付款構成了你的帳戶淨值,而首付款加上抵押貸款價值構成了相當於一個投資組合的規模。因此,一套20萬美元的房子(抵押貸款15萬美元)首付5萬美元就構成了(15萬+ 5萬)/5萬= 4的槓桿。因此,在這種情況下,你在房子上的槓桿是4倍。保證金賬戶的投資組合表現類似。有一個“現金”組成部分,然後更多的股票可以通過保證金貸款來提供槓桿作用。
在我們陳述凱利準則之前,我想特別概括一下推導過程中的假設,這些假設有不同程度的準確性:
● 每個算法交易策略將被假定擁有一個正態分佈的回報流(即高斯)。此外,每種策略都有其固定的收益均值和標準差。該公式假設這些平均值和std值不變,即它們在過去和將來是相同的。這顯然不是大多數策略的情況,所以要注意這個假設。
● 這裡考慮的回報是超額回報,這意味著它們扣除了所有融資成本,如保證金利息和交易成本。如果該策略是在機構環境下實施的,這也意味著回報是扣除管理和績效費後的淨額。
● 所有的交易利潤都進行了再投資,沒有提取淨值。這顯然不適用於扣除上述管理費、投資者經常撤資的機構。
● 所有的策略在統計上都是獨立的(策略之間不存在相關性),因此策略收益之間的協方差矩陣是對角的。
現在我們來看看實際的凱利準則,假設我們有一組N種算法交易策略,我們希望確定如何為每種策略應用最優槓桿以使增長率最大化(但將回撤降至最低),以及如何在每種策略之間分配資本。如果我們將每個策略i之間的分配表示為長度為N的向量f,使得 ,則每個策略
最優分配的Kelly準則為:
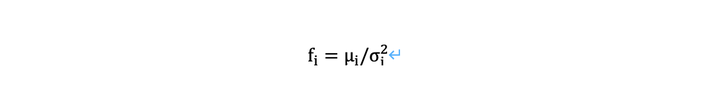
策略i中為平均超額收益和
為超額收益的標準差。這個公式基本上描述了最優槓桿應該應用於每個策略。
雖然Kelly準則給出了最優的槓桿率和策略配置,但我們仍然需要實際計算出投資組合的預期長期復合增長率,我們用g表示,其公式為:
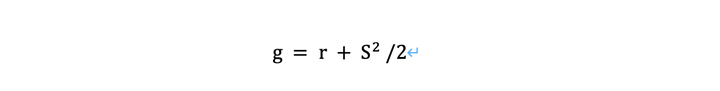
其中r是無風險利率,也就是你可以從經紀人那裡借錢的利率,S是策略的年度夏普比率。後者是通過年度平均超額回報率除以年度超額回報率標準差計算出來的。有關夏普比率的詳情,請參閱前一章有關業績衡量的內容。
一個現實的例子-讓我們考慮一個例子在單一策略情況下(i = 1)。假設我們做多一個神話般的XYZ股票平均年回報率m = 10.7%,年度標準差σ= 12.4%。此外,假設我們能夠以無風險利率r = 3.0%借款。這意味著平均超額收益是µ = m − r = 10.7 − 3.0 = 7.7%。這給出了S = 0.077/0.124 = 0.62的夏普比率。
這個我們可以計算最優凱利槓桿通過 = 0.077/0.1242 = 5.01。因此Kelly槓桿說,對於一個10萬美元的投資組合,我們應該額外借入40.1萬美元,使總投資組合價值為501,000美元。在實踐中,我們的經紀公司不太可能讓我們有這麼大的保證金交易,所以凱利標準將需要調整。
我們可以用夏普比率S和利率r來計算長期復合增長率g。 == 0.22,即22%。因此,我們應該期待這一策略每年22%的回報。
更多內容請關注公眾號【火象】~












