由Flashbots 開創的MEV競拍服務已受到了礦工們的歡迎,那麼這種競拍是否是最優的呢?

在包(Bundle)分配問題中,礦工面臨著固定數量的交易,而他們要將這些交易包含在給定的區塊中,此外,礦工還可以選擇在該區塊中包含(或排除)哪些包(Bundle)。礦工通過將每個包(Bundle)包含在區塊中來賺取利潤,然而,包(Bundle)具有很多必須要考慮的分配約束。在這篇文章中,我們給出了一個簡單的整數線性規劃問題(ILP)公式,並提供了一些基本的擴展。
簡介
礦工可提取價值(MEV)這個術語,指的是礦工根據交易排序可獲得的任何超額利潤。在區塊鍊等去中心化系統中,用戶通過點對點的gossip網絡向礦工提交一組交易和費用。而礦工們會收集這些交易,並將它們分批成一個完全有序的序列,然後由大多數礦工驗證並接受作為下一個區塊。
然而,在很多區塊鏈中(例如以太坊),礦工可選擇要包含的交易集以及提交交易的順序。
如果一名礦工提交一筆具有經濟意義的交易,他們可以對交易重新排序以確保他們的交易首先執行,這也被稱為搶先交易(front running)。自從MEV這一概念被提出以來,已經出現了很多涉及閃電貸、借貸以及三明治攻擊的新型MEV 形式。 MEV代表了一種價值提取形式,而用戶無法通過簡單地修改其交易競價行為來消除它。
公平(Fairness)。從理論上講,MEV 可能導致區塊鏈共識不穩定,並可能迫使用戶在預期交易費用之外支付額外的費用來處理交易。這也引出了很多研究,而這些研究的重點是保證交易排序及包含方面的“公平性”。而公平算法嘗試使用密碼學方法,例如對交易排序或待處理交易狀態的時間鎖承諾(time-locked commitments),以強制基於時間的“公平”保證。
MEV競拍。或者,有一些研究工作表明,MEV是區塊鏈獨有的,它無法通過純粹的密碼學方式刪除。這一系列工作有效地表明,相比用密碼學方式刪除MEV,礦工和用戶共享MEV利潤將導致穩定的均衡。
在這個由Flashbots 開創的世界中,“探索者”試圖找到交易的最佳順序,然後競標由礦工以特定順序執行的“包”交易。這種出價通過MEV 拍賣進行調解——即參與者願意在鏈下拍賣中向礦工支付額外的優先出價。因此,MEV競拍是更受歡迎的,並且這種方式在2021 年為礦工創造了超過7 億美元的額外收入。
最優性(Optimality)。然而,一個自然要問的理論問題是,這種競拍是否是最優的呢?目前,Flashbots競拍通過使用約束求解器解決背包問題(Knapsack problem)來有效地執行交易包(bundle)。但是從理論上講,我們應該期望近似整數線性規劃(ILP) 的解決方案是“最優”的嗎?應該如何描述最優性?由於MEV 是根據所有資產的可提取價值來定義的,因此任何最優概念都取決於任何一組交易和包(bundle)可實現的最大利潤。
總結(Summary)。在這篇短論文中,我們給出了在單個區塊中包含交易包(bundle)的最優ILP的首個正式描述。我們的描述側重於MEV 的三種操作形式,包括搶先交易(front running)、尾隨交易(back running)以及三明治交易(sandwiching)。我們假設在實踐中使用的精確gas模擬方法是作為預處理步驟執行的,它將分配問題(尋找最優包分配的問題)與正確估計單個包(bundle)利潤的問題解耦。我們的公式可以很容易地用高級描述語言(例如CVXPY)進行優化並在實踐中使用。
1 定義
在這節內容中,我們首先來描述一下這篇論文中使用的基本定義。
交易(Transaction):礦工通常從一系列的交易開始,我們把這些交易寫成一些集合T(將包含在區塊中)。這些交易由區塊鏈的用戶提供,它們可以是Uniswap 或Curve的swap交易、借貸或預言機更新等交易。
包(Bundle):礦工還接受許多由用戶提交的包(Bundle),所謂包(Bundle)是一個帶有關聯交易的操作(action,我們稍後定義),每個包(Bundle)還包括了一些出價,例如,用戶願意支付多少錢才能將其包(Bundle)包含在區塊中。礦工可以決定區塊中包含哪些包(Bundle)以及交易。而礦工從包(Bundle)中獲得的利潤,等於區塊中包含的各個出價的總和。
操作(action):從以前開始,每個包(Bundle)都將一個操作(action)與一筆交易(t ∈ T)相關聯。可能的操作(action)是:搶先交易t(在t之前執行一筆交易),尾隨交易(在t 之後立即執行一筆交易),以及三明治交易(在t前後都執行一筆交易)。
對於給定的交易t ∈ T,要么是進行三明治交易t,要么是進行搶先交易以及尾隨交易t。例如,如果有三個包(Bundle)與交易t關聯,其中一個在t之後進行尾隨交易,一個執行搶先交易,另一個執行三明治交易,那麼礦工可以選擇包括搶先交易包(Bundle)和尾隨交易包( Bundle),或者是三明治交易包(Bundle),但不能同時包括這兩個類型。
我們把這三個操作的空間稱為A。現在我們可以很容易地將包(Bundle)定義為與交易t ∈ T 相關聯的操作(a ∈ A),而它會有一個出價金額( p > 0)。即包(Bundle)是一個三元組(a,t, p) ∈ A × T × R+,所有包(Bundle)的集合將由B ⊆ A × T × R+ 給出。
利潤最大化(Profit maximization)。剩下的問題是:礦工如何選擇哪些交易包含在他們的區塊中,以實現利潤最大化?在下一節中,我們將展示這一問題可表述為一個簡單的整數線性規劃問題(ILP),而其通常可通過現代計算機在合理的時間內解決。
2 問題表述
我們將利潤最大化問題表述為整數線性規劃(ILP),我們將其稱為包(Bundle)分配問題。
設置函數。為方便起見,我們將編寫定義以下函數。這裡,t ∈ T是一筆交易,而B是所有包(Bundle)的集合。
我們將s(t)定義為與三明治交易t關聯的包(Bundle)集合:
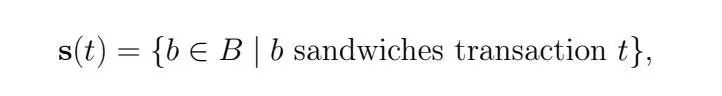
類似地,f(t)是與t相關聯的搶先交易,b(t)是與t相關聯的尾隨交易。我們假設B 由b = 1, 2, ... 索引,其中n 是提議的包(Bundle)的數量。
問題陳述:將包(Bundle)分配問題寫成整數線性規劃問題的一種簡單方法如下:
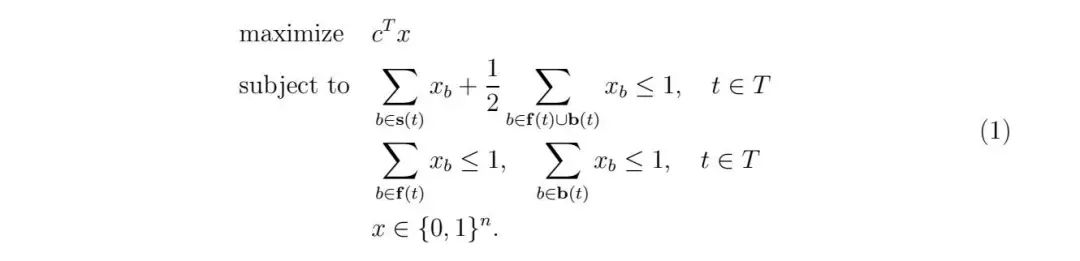
這裡,
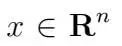
是優化變量,如果當前區塊中應包含包(Bundle)b,則xb為1,否則為0。問題數據是

,這是一個向量,使得cb ≥ 0 是礦工在他們的區塊中包含包(Bundle)b所獲得的利潤,而T是要包含在此區塊中的交易集(不包括包(Bundle)) 。
標準形式。問題(1) 可以用矩陣表示法寫得更簡潔一些。為此,我們將定義m = |T|,交易總數,以及矩陣
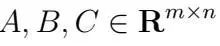
為:
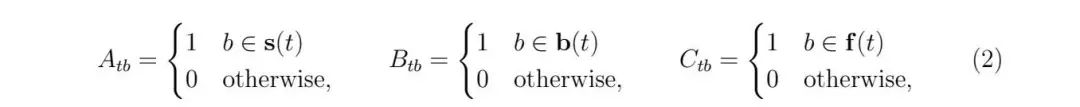
對於每筆交易t∈ T和包(bundle)b ∈ B,使用這些新的定義,問題(1)可用以下方式編寫:
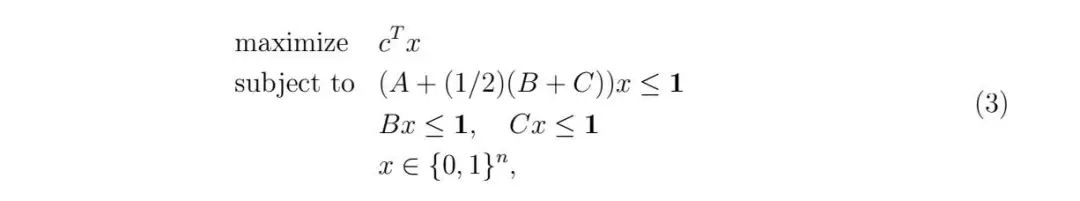
其中1是適當維度的全1向量,而
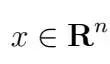
是優化變量。
解釋。我們可以將目標和約束解釋如下。目標
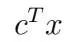
僅僅是包含在區塊中的包(bundle)給出的利潤總和。第一個約束意味著區塊中最多包含一個三明治包(bundle),或者區塊中最多包含兩個搶先交易或尾隨交易t的包(bundle)。第二個約束意味著對於每筆交易t,最多包含一個搶先交易包(bundle),以及最多包含一個尾隨交易包(bundle),而最後一個約束是將x的條目約束為布爾值。
放寬鬆。一般來說,除了非常小的實例之外,問題(1) 可能很難解決,因為x的條目有布爾約束。但是,在許多實際情況下,將布爾約束放寬為邊界約束(box constraint,即0 ≤ x ≤ 1),經過一些簡單的捨入方案後,可以產生合理的實際性能以及合理的解決方案。一般來說,這個寬鬆問題的最佳目標,始終是礦工可能獲得的最大利潤的上限,而任何舍入方案都會給出一個下限。這可以用來給出所提議的包(bundle)分配的次優程度的一個界限。例如,如果放寬後的利潤為1.2 ETH,而擬議分配的利潤為1 ETH,則擬議分配的次優性最多為1.2/1 − 1 = 20%。換句話說,最多可將提議的分配提高20%。
2.1 擴展
問題(1)有幾個簡單但非常有用的擴展。
包(bundle)約束。例如,用戶可能希望指定幾個包(bundle),這些包(bundle)必須由礦工一次性全部包含,或者根本不包含。我們可以把它寫成包(bundle)Bi ⊆ B的子集。對於i = 1, 。 . . , ℓ,如果Bi中包含任何一個包(bundle),則礦工必須包含包(bundle)Bi的整個子集。
新的優化問題由下面的公式給出:

其中優化變量是
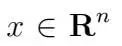
和
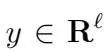
,而問題數據是在(2) 中定義的矩陣
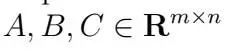
和矩陣
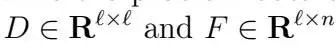
:
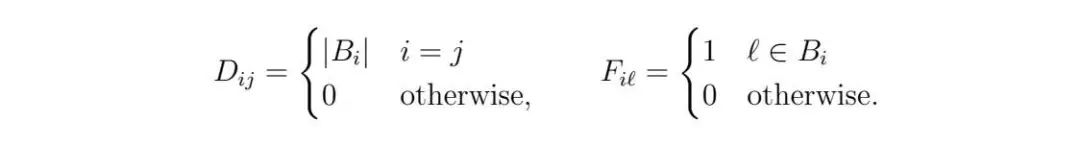
換句話說,D是一個對角矩陣,其對角條目是集合Bi的大小,而F 是一個矩陣,使得(Fx)i 給出了Bi 中要包含在區塊中的包(bundle)的數量。約束Fx=Dy簡單地表示,對於每個可能的i,要么包含所有| Bi | 包(bundle),要么只包含0個包(bundle)。
gas限制。另一種可能(且非常簡單)的擴展,是在優化問題上包含總gas約束。例如,當包含在區塊中時,每個包(bundle)b ∈ B可能使用一些最大量的gas(由gb ≥ 0給出)。我們可以很容易地附加約束,即包(bundle)使用的最大gas 總量不超過交易(但不包括包(bundle))執行後剩餘的gas 量;即
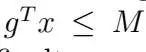
,其中M ≥ 0 是剩餘的gas量。我們注意到,這可能是一個很難獲得合理限制的數量,因為當區塊中包含包(bundle)時,交易使用的gas可能會發生巨大變化。有其他可能的方法來進行計算,但我們不在這裡討論它們。
3 結論
在這篇論文中,我們提供了一個簡單但非常通用的公式,它可以用於解決礦工利潤最大化包(bundle)分配的問題。雖然該問題通常是NP問題,但我們懷疑大多數整數線性規劃求解器(甚至線性規劃鬆弛)在實際情況下可能有很好的表現。














