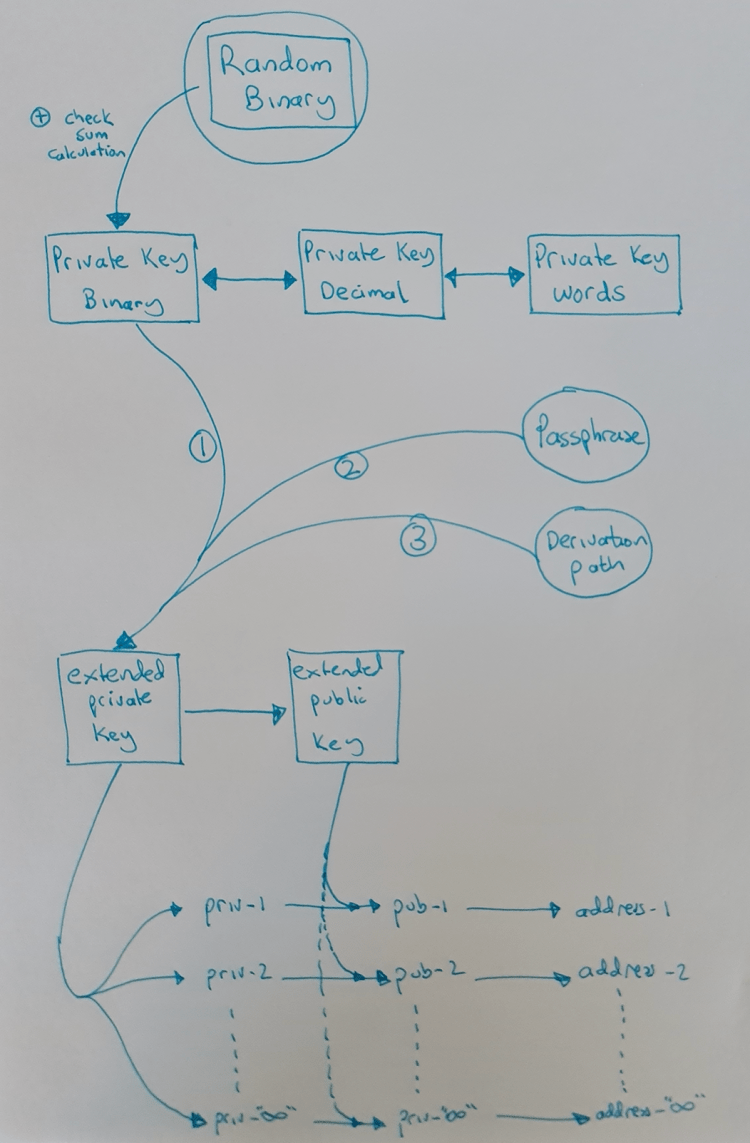
凡是關心自己的比特幣財產安全的人都應該試著理解下圖:
數字
如果你完全理解二進制、十進制和十六進制,可以跳過這部分。
十進制指每一位數都有10 種可能(0、1、2、3、4、5、6、7、8 或9)。數字“6.15” 有3 位數(順帶一提,6.15 這個數字是有特殊含義的,即,每個人都應該努力擁有6.15 個比特幣)。第一個數是“6”,第二個數是“1”,第三個數是“5”。這三個數可以是0、1、2、3、4、5、6、7、8、9 中的任何一個。
在十進制中,我們從“0” 數到“9”(0、1、2、3、4、5、6、7、8、9)就沒有新的數了,接下來就要在左邊新增一位“1”(即,逢十進一),得到“10”,然後再從“0” 開始數起—— 原先的“9” 進了一位,十位數變成了“1”,個位數變成了“0”。
二進制指每一位數只有兩種可能(“0” 和“1”)。
在二進制中,我們從“0” 數起,然後是“1” ,接著就是“10”!看見沒?如果你覺得跨度很大,那是因為你還沒有跳出十進制思維。
在十進制中,“10” 就是普通人的手指數量—— 因為我們有10 個手指,所以我們人類常用10 進制。
但是,在二進制中,“10” 就是一個人的大拇指的數量。想像一下用你的大拇指數數:1、10、11、100、101、111、1000、1001…… (譯者註:這幾個數字換算成十進制就是1、2、3、4 ……)
如果這是你第一次了解二進制,可以用紙和筆自己算一下,可能會有幫助。這就像是第一次學習數數那樣,而且還不能靠直覺。
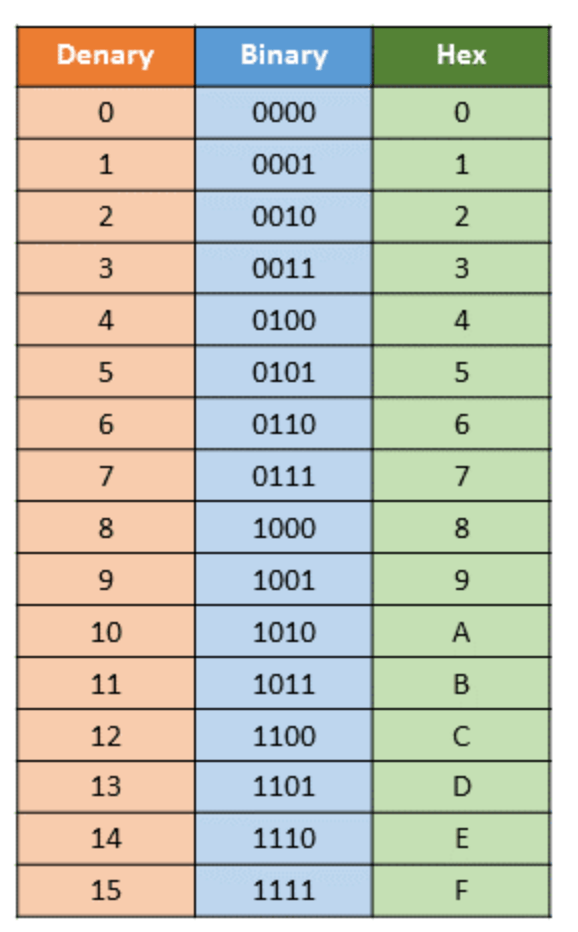
十六進制指每一位數有16 種可能(0、1、2、3、4、5、6、7、8、9、a、b、c、d、e、f)。其中,a=10、b=11、c=12、d=13、e=14 和f=15。
就像撲克牌遊戲一樣,Jack=11、Queen=12、King=13、Ace=14 或1。一個字母可以代表一個數字,這就是關鍵。
每一位數的可能性越多,表達一個大數字所用的位數就越少。例如,十進制下的2047 ,寫成二進制就是11111111111(11 位數),寫成十六進制就是7FF。
總結:
隨機二進制數、校驗和、私鑰
私鑰首先是一個二進制數,可以轉換成其它形式。但是,私鑰本質上是二進制數,因為它是為了給計算機使用的。下面是二進制私鑰的一個例子:
01000011111 10101110110 01001000001 01001101000 10000100011 10001011011 00100110111 11010000011 11001000001 10111110010 00010101000 00101110110 01100001101 11000010011 01101111001 11001010111 10011010000 01001110000 01000010010 00001110011 10011110101 11000110011 10101101110 00100111111
請注意,這個私鑰由24 組數字組成,每11 個數字為一組,共計264 個二進制數字(24×11=264)。
計算機看到的私鑰雖然是同一串數字,但是沒有空格:
010000111111010111011001001000001010011010001000010001110001011011001001101111101000001111001000001101111100100001010100000101110110011000011011100001001101101111001110010101111001101000001001110000010000100100000111001110011110101110001100111010110111000100111111
這是個很大的數字,寫成十進制就是:
7,869,270,257,961,728,227,967,109,454,183,816,220,476,881,432,001,550,169,555,390,346,110,510,455,025,983
請注意這兩個數的值是一樣的,區別只在於十進制寫起來更短。
總之,私鑰有一部分是隨機生成的,而最後8 位(叫作校驗和(checksum))是以前面的隨機部分作為輸入通過一個公式計算得出的。這是一種(軟件錢包共同認可的)工程設計:如果數據輸入不正確,計算機就會發現校驗和與輸入數據不匹配,並警告用戶。錢包會提示“抱歉,您的輸入可能有誤” 。當然,用戶可以強行選擇繼續。校驗和並非比特幣代碼的一部分,是為了保障用戶安全而引入的。
換言之……從數學設計上來講,在創建私鑰時,下面這個隨機部分……
01000011111 10101110110 01001000001 01001101000 10000100011 10001011011 00100110111 11010000011 11001000001 10111110010 00010101000 00101110110 01100001101 11000010011 01101111001 11001010111 10011010000 01001110000 01000010010 00001110011 10011110101 11000110011 10101101110 001
只會生成下面這個校驗和……
00111111
把二者結合起來就得到了最終的私鑰。點擊此處,了解私鑰是怎麼來的,以及校驗和是如何計算的。請注意,8 位數的校驗和與末尾3 個隨機數字組合起來剛好是一組11 位數字,與其它幾組一樣(在BIP39 標準下,一個單詞需要11 位數表達,詳見下文)。
不同的 隨機 二進制數會產生不同的校驗和。假設用戶在錢包裡輸入私鑰,並聲稱“這是我之前生成的私鑰,請顯示我的地址”,只要有一位數字錯誤,軟件錢包都會發現並發出警告。
請原諒我有些囉嗦,但是掌握這些背景知識真的很重要。
私鑰轉換
人類很難準確記錄下一個二進制私鑰並將其輸入軟件錢包。一旦發生錯誤,就有可能導致比特幣丟失。手寫無法使用校驗和來檢查錯誤,只有輸入計算機才可以。
一種解決方案是將二進制數轉化成十進制數,讓私鑰變得更短、更好記。
假設一個二進制數被切分成每11 個數字一組,則每一組數最多可以表示2048 個十進制數(可表示的十進制數範圍是“0” 至“2047”)。 “0” 至“2047” 轉化成二進制就是“00000000000” 至“11111111111”。
我們可以將這個私鑰轉換成24 組十進制數,每組十進制數的範圍是“0” 至“2047”。這樣寫起來容易,但還是容易出錯。
BIP39 可以有效化解這一風險。這個協議建議比特幣用戶使用一列由協議定義過的單詞表,我猜測這些單詞是經過精挑細選的,以防被誤讀成其它單詞。
BIP 39 單詞表共包含2048 個單詞,按照字母順序排列。點擊此處,查看列表。除了英文版,還有其它語言版本。每個單詞都代表“0” 至“2047” 之間的某個數字。這樣一來,私鑰中的每個十進制數都可以被寫成一個單詞。數字和所對應的單詞之間有什麼特殊聯繫嗎?沒有,這只是由協議定義的,只要我們都使用這個協議,那麼單詞與數字之間就可以畫上等號。
這就是助記詞(seed words)的由來。你在軟件錢包中輸入助記詞後,每個單詞都會轉化成11 個二進制位,將它們組合起來就會形成一個264 位的二進制數,也就是私鑰(還記得嗎?最後一個單詞包含校驗和,因此不是隨機的)。如果是由12 個單詞組成的助記詞,私鑰的長度只有一半,也就是132 位。
遺憾的是,原始的BIP 39 單詞表存儲在GitHub 內,代表的十進制數範圍是“1” 至“2048”,而非“0” 至“2047”。這只是Github 格式的問題,而非有意設計成如此。
為了清楚地說明這個問題,我們來舉個例子。假設某個私鑰的開頭是11 個“0”,例如“00000000000”,那麼我們要用單詞表上的第一個單詞來表示這個二進制數。第一個單詞是“abandon”,表示的是“00000000000”,但是被標記成了“1”。這是不對的。十進制數“1” 轉化成二進制是“00000000001”,這不是我們想要的。但是,由於格式的問題,單詞表上所有單詞的序號都比它們實際代表的十進制數大了“1”。
我們還可以通過拋硬幣來生成二進制數。計算機可以幫助我們獲得使用斜體表示的最後8 位數:
010000111111010111011001001000001010011010001000010001110001011011001001101111101000001111001000001101111100100001010100000101110110011000011011100001001101101111001110010101111001101000001001110000010000100100000111001110011110101110001100111010110111000100111111
我們首先要做的,是將這個二進制數按照每11 個數為一組進行切分:
01000011111 10101110110 01001000001 01001101000 10000100011 10001011011 00100110111 11010000011 11001000001 10111110010 00010101000 00101110110 01100001101 11000010011 01101111001 11001010111 10011010000 01001110000 01000010010 00001110011 10011110101 11000110011 10101101110 00100111111
接下來,我們將每一組數轉化成十進制數:
543, 1398, 577, 616, 1059, 1115, 311, 1667, 1601, 1522, 168, 374, 781, 1555, 889, 1623, 1232, 624, 530, 115, 1269, 1587, 1390, 319
然後,我們查詢這些十進制數在單詞表上對應的單詞:

考考你:十進制數543 對應的是哪個單詞? Dry、duck 還是dumb?
上圖是從Github 上截取的,因此這張單詞表的序號是從“1” 開始的。因此,每個序號都減去“1” 之後才是每個單詞真正對應的十進制數。因此,序號544 的單詞dumb 實際上代表的是“543”,也就是我們要找的那個單詞。
第二個數是1398,對應的是單詞表上序號為1399 的單詞。
全部轉化為單詞後就是:
dumb put else escape love merge cheap spare sight salad bench conduct giant second hundred slab old evoke drastic attack pact shoe punch child
請注意,所有單詞都是按字母排序的,首字母越靠前的單詞代表的數字越小,首字母越靠後的單詞代表的數字越大。當你明白這些單詞的排序規律之後,可以明顯看出這點。
擴展私鑰
再來看下面這張圖:
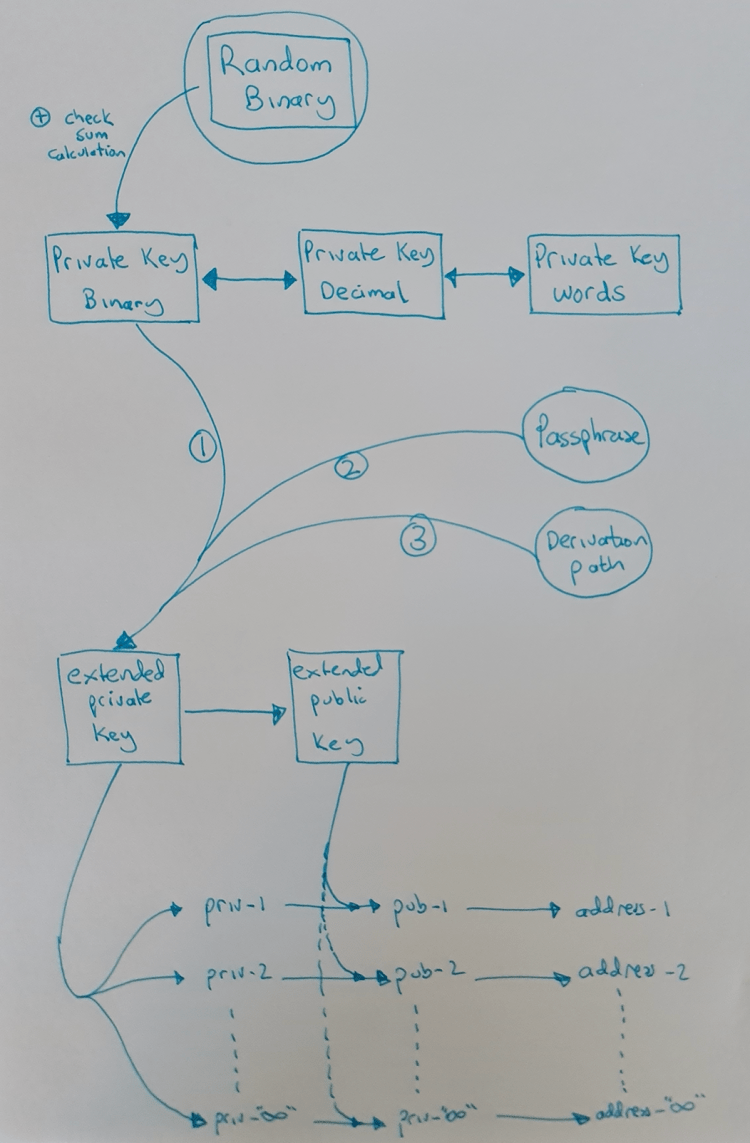
擴展私鑰是使用二進制私鑰以及密語(passphrase)和衍生路徑(derivation path),根據你我都沒必要知道的數學公式計算得出的。
請注意增加密語是如何徹底改變下游擴展私鑰的。修改衍生路徑也會改變下游數據。不要小看了你的軟件錢包提供的默認衍生路徑,請務必把它寫下來保存好。我會另外寫一篇文章來詳細介紹衍生路徑。
擴展私鑰最終用來生成一個錢包中的所有比特幣地址,而且可以花費這些地址上的比特幣。如上圖所示,擴展私鑰可以生成多個獨立私鑰(不是擴展私鑰,而是普通的私鑰),每個私鑰會生成獨立的公鑰,每個公鑰又會生成一個地址。
擴展私鑰還可以用來生成接下來要詳細討論的擴展公鑰。
我們無法根據單個獨立私鑰倒推出擴展私鑰。這是我個人的理解,但是我不是密碼學專家,因此不能確定,不過這麼想很合理。但是,每個獨立私鑰有可能指向後一個獨立私鑰,當然這點我也不確定。因此,為確保萬無一失,別向任何人洩漏你的任何一個私鑰。
可以確定的是,任何一個公鑰都不會洩漏其對應的私鑰。明白這一點很重要。
我在 https://iancoleman.io/bip39/ 上生成了一個測試錢包。這個網站是練習生成虛擬錢包的好地方(千萬別在聯網的電腦上使用這種方式生成真的錢包)。
擴展私鑰如下所示:

請注意,上圖顯示的是“賬戶” 擴展私鑰。我不知道這個網站為什麼要這麼標記。
再來看這個擴展私鑰的開頭是“x”。這意味著使用這個私鑰將生成以“1” 開頭的傳統地址。傳統地址也叫作P2PKH(pay to public key hash,支付到公鑰哈希值)地址。
使用以“y” 開頭的私鑰(或公鑰)會生成以“3” 開頭的地址。這些地址也叫作P2SH(Pay to script hash,支付到腳本哈希值)地址。
使用以“z” 開頭的私鑰會生成原生的segwit/Bech32 地址。這類地址以“bc1q” 開頭。
最後,以大寫字母“X”、“Y” 或“Z” 開頭的私鑰會生成多簽錢包的地址。
擴展公鑰
擴展公鑰的用途不是很明顯。如果你仔細看示意圖的底部,你會發現使用擴展公鑰通過錢包軟件生成的比特幣地址與使用擴展私鑰生成的一樣,而且地址順序相同。使用擴展公鑰和擴展私鑰生成的錢包看起來完全一樣。那麼區別在哪兒呢?
使用擴展私鑰生成的錢包能夠進行支付。
使用公鑰生成的錢包無法進行支付。這種錢包通常被稱為“觀察” 錢包。你可以將這個錢包放在安全性低的計算機上,不用擔心會丟失私鑰,但可以用來查看你的錢包餘額,或是複制地址發送給其他人。
但你還是應該注意保護好自己的擴展公鑰。一旦洩漏,其他人就可以通過訪問你的擴展公鑰來查詢你的錢包餘額和你的所有地址。從今往後,他們都可以查詢你的錢包餘額,就好像查詢你的銀行賬單一樣。
保護好你的金融隱私,更要保護好你的金融密鑰(比特幣私鑰)。
注:擴展公鑰如下圖所示:

如上圖所示,公鑰不是以“xprv” 開頭,而是以“xpub” 開頭,另外也可以“ypub”、“zpub”、“Xpub”、 “Ypub” 和“Zpub” 開頭。 (大寫指的是多簽私鑰。)
總結
我希望這篇文章能幫助你理解比特幣的公鑰和私鑰,進而讓你更容易理解比特幣的運作原理。
如果你有任何問題,請聯繫我,或閱讀我的輔導材料。
讀懂了這篇文章會讓你更容易理解如何通過擲骰子的方式生成助記詞,多簽錢包的生成以及 PGP 加密。
補充閱讀
點擊此處,了解什麼是衍生路徑。
(完)
(文內有許多超鏈接,可點擊左下”閱讀原文“ 從EthFans 網站上獲取)
原文鏈接:
https://armantheparman.com/public-and-private-keys/
作者: Arman The Parman
翻譯&校對:
閔敏&阿劍















