Paradigm发布文章“Variable Rate GDAs”，提出一种新的NFT发行机制，可根据销量调控发行速度。原文还对该机制进行了讲解，由Transmissions11、Frankie和Dave White撰写，PANews Zen对其进行了编译。
概述
本文介绍了一种专为由实验性艺术工厂Art Gobblers设计，并可在Paradigm旗下PVP赛车竞赛项目0xMonaco中使用的新型代币发行机制：可变利率GDA (VRGDA)。该机制可概括为，根据实际销售水平与既定销售目标之间的背离调整 NFT 售价，以加速完成销售目标，或减速放缓销售进度，最终使得整个项目的发行节奏与预期的销售计划相符。
除了该机制的概述，Paradigm还讲述了高度优化、可用于稳定生产的核心机制，以及几个示例。
动机
Art Gobblers是Justin Roiland和Paradigm创建的数字艺术实验项目。该项目的一个重要目标是创建一个自给自足的生态系统，使之可以在未来几年内无需人工干预而自行发展。这个系统中有两个核心NFT，他们希望任何人都可以随时购买。
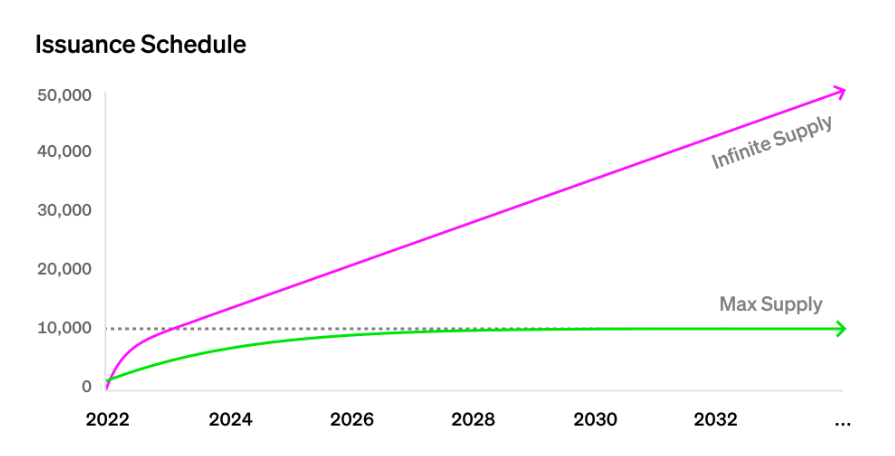
起初，Paradigm计划较快地发行这两个NFT。随着时间的推移，一个以固定的供应量达到顶峰，而另一个则永远以缓慢的恒定速率发行。Paradigm力求实现这些目标，同时保持无缝的用户体验，让用户可以随时购买NFT，而无需按时等待预定的拍卖。解决方案VRGDA由此应运而生，它是泛化版的GDA，允许用户在任意时间发行NFT，而不是按照规划与进度，标准化且线性地进行GDA。
机制
建立直觉
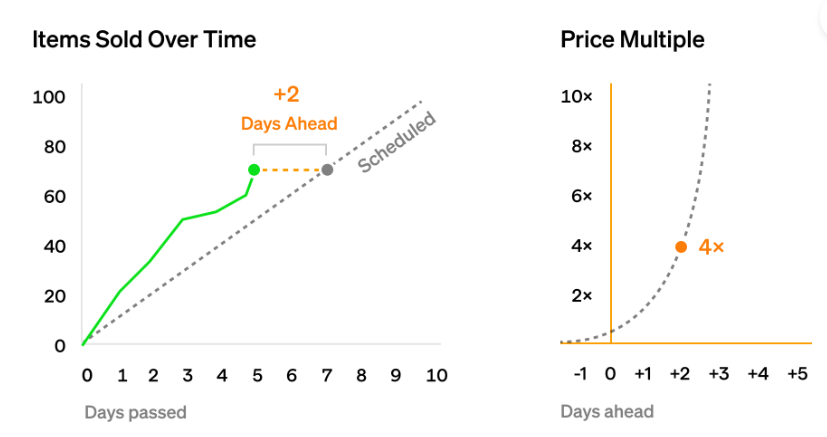
想象这么一个简单的计划表，我们希望每天销售10个NFT，并为第一个NFT设置了1代币的起始价格。假设到了第5天，那么我们应该已经卖出50个NFT。但是由于这几天市场需求很高，我们早已卖出了70个，本来计划是7天的销售量，我们提前两天完成。故而我们会希望在未来以更高的价格进行售卖。这就需要使用指数曲线来确定究竟应该高多少，这个结果会因参数而异。但在这种情况下，假设我们使用“提前两天"的参数 ，因此我们以“22=4”的倍数来提高价格，所以在初始价格是1个代币的基础上，新价格将是4个代币，这使得购买更多NFT变得更加困难。假设又过了10天后，即在第15天时，按计划本我们应卖出150个NFT，但用户只购买了120个，这是在第12 天就应该达到的数量，意味着我们落后于计划三天。所以我们可以将价格调整为原来的2-3=0.125倍，方便用户购买更多的 NFT。
建造
参数
P0：按照计划以完美的进度售出NFT时的售价（即目标价格）。
k：在没有用户购买的情况下，NFT价格在单位时间内下降的百分比。
f(t)：表示在t时计划出售NFT的目标数量。
客观情况
我们希望按特定时间表发行NFT。我们将使用的机制是，如果NFT出售速度超出预期，则提高价格，如果NFT出售速度相较滞后，则降低价格。如果销售完全按计划进行，则保持当前价格不变。
定义
假设我们想按照f(t)描述的时间表出售NFT，该时间表将一个时间点映射到那时我们想要出售的NFT的累积数量。例如，如果我们想每两天卖出一个NFT，我们会这样定义：f(t)=t/2
假设我们通过独立的GDA来售卖每个NFT。如果我们将每个NFT的起始价格设置为1，并让该价格在没有销售的情况下以每单位时间k的速率衰减，则在t时的购买价格将是：(1-k)t
为了给自己实现目标所需的灵活性，我们可以将拍卖的起点在时间上移动至Sn，由此可推导出该NFT在t时刻的价格是：
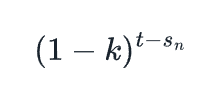
如果我们希望我们的目标价格不同于 1，我们可以乘以一个常数p。我们称之为调整后的价格vrgdan(t)为：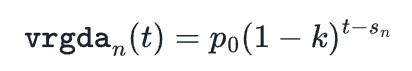
决定Sn
根据我们的发行时间表f，我们想在tn时卖出第n个NFT。我们可以通过用f来反推tn，从而得出第n个NFT被出售的具体时间为：tn=f -1(n)
VRGDA目标的一个结果是，如果第n个NFT根据其发行时间表在目标时间准确购买，其价格将为P0。正式表达，这意味着如果我们以准确的目标价格出售，那么在时间tn，第n个NFT的定价将为：
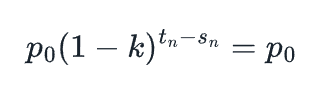
通过除法进行简化，我们知道以下内容应该始终成立：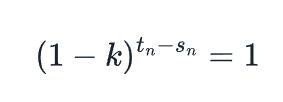
这意味着tn - Sn=0或Sn = tn，使用我们上面tn的定义，可得知Sn=f -1(n)。
最终公式
通过将Sn的定义代入vrgdan(t)，我们最终得到最终公式：
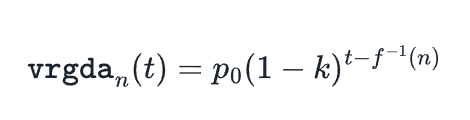
简单的发行时间表
下面我们演示推导一些简单的发行时间表以与 VRGDA 公式一起使用。
线性
假设我们想每天出售r个NFT。则有f(t)=rt，那么f -1(t)=t/r
将f -1(t)代入VRGDA定价公式后，我们得到以下结果：
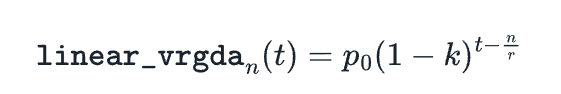
请注意，这与GDA同构，这也是称VRGDA为GDA的泛化的原因。
平方根
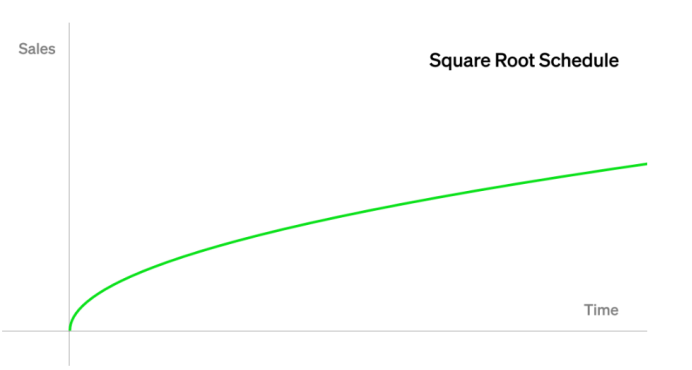
假设我们希望以与时间的平方根成正比的速率发行NFT。例如，一开始以较快的速度发行NFT，然后随着时间的推移而变慢，但永远不会停止。
然后我们可以设置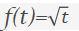
，这样在第1天我们卖出了1个 NFT，在第4天我们卖出了2个，在第9天我们卖出了3个，依此类推。
在这种情况下，f -1(n)=n2。现在我们只需插入VRGDA定价公式即可获得：
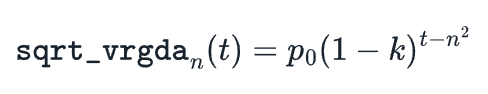
模型发行时间表
与上述示例相比，模型发行计划有些复杂。然而，我们仍然选择详细介绍它，因为它提供了一种在不强制实施无限通货膨胀机制的情况下引导初始增长的方法。
动机
假设我们一开始想快速发行NFT，然后放慢速度，直到最终发行了某个最大数量，正如Art Gobblers中的情况一样。
对此进行建模的一种简洁方法是使用具有正域的逻辑函数。
导出f
逻辑函数是一个 S 形曲线。我们将稍微简化一下并将其定义为：
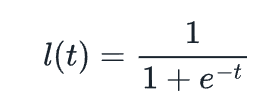
这条曲线在接近负无穷时接近 0，在接近无穷大时接近 1。
对于我们的特定应用程序，我们不想使用完整的 S 曲线（尽管也可能有一个完整的逻辑 VRGDA，它会开始缓慢、加速，然后再次减速）。相反，我们只想使用曲线中为正的部分。
因为l(0)=0.5，但是我们希望我们的时间表显示时间为0时卖出0个NFT，我们需要通过减去0.5来将此函数曲线向下移动。这条新曲线将从0变为0.5：
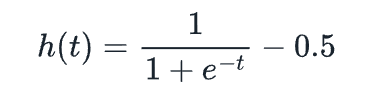我们想要发布L-1个NFT（我们选择这个是为了记号方便，因为该函数会在到达L之前与之渐近），因此我们需要将该函数乘以2L。
我们还可以引入一个时间尺度参数来调整发行 NFT 的速度：
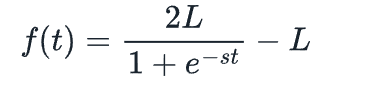
采摘
要选择s，请注意：
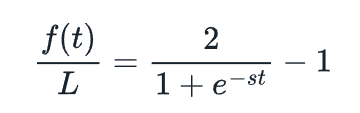此外：
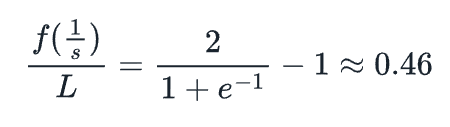这意味着我们可以通过选择大约期望值的46%的nft发行的时间来选择s。例如，如果我们希望在100个时间单位后发行46%的 NFT，这意味着1/s=100，所以s=1/100。
公式
取上述收益率f(t)的倒数：
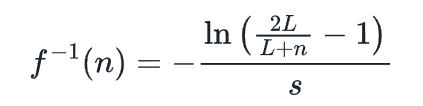
综上所述，我们最终得到以下公式：
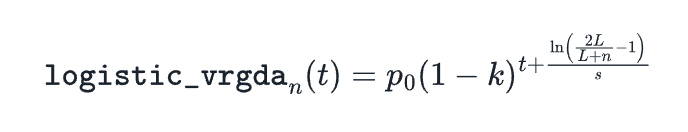
执行
可以在传输11/VRGDA 上找到高度优化、生产就绪且获得许可 (MIT) 的 VRGDA 实施和各种发行时间表。欢迎使用改进的拉取请求。
结论
VRGDA提供了一种使用几乎任何您想要的时间表发行NFT的方法，同时仍然允许用户随时无缝地购买它们。在Art Gobblers的案例中，它们使我们能够定制我们的社区增长和UGC动态。以0xMonaco为例，它创造了一个具有挑战性且竞争激烈的游戏循环。我们相信它在NFT、链上游戏、DeFi等领域还有许多其他潜在应用。
APP 
