Paradigm發布文章“Variable Rate GDAs”，提出一種新的NFT發行機制，可根據銷量調控發行速度。原文還對該機制進行了講解，由Transmissions11、Frankie和Dave White撰寫，PANews Zen對其進行了編譯。
概述
本文介紹了一種專為由實驗性藝術工廠Art Gobblers設計，並可在Paradigm旗下PVP賽車競賽項目0xMonaco中使用的新型代幣發行機制：可變利率GDA (VRGDA)。該機制可概括為，根據實際銷售水平與既定銷售目標之間的背離調整NFT 售價，以加速完成銷售目標，或減速放緩銷售進度，最終使得整個項目的發行節奏與預期的銷售計劃相符。
除了該機制的概述，Paradigm還講述了高度優化、可用於穩定生產的核心機制，以及幾個示例。
動機
Art Gobblers是Justin Roiland和Paradigm創建的數字藝術實驗項目。該項目的一個重要目標是創建一個自給自足的生態系統，使之可以在未來幾年內無需人工干預而自行發展。這個系統中有兩個核心NFT，他們希望任何人都可以隨時購買。
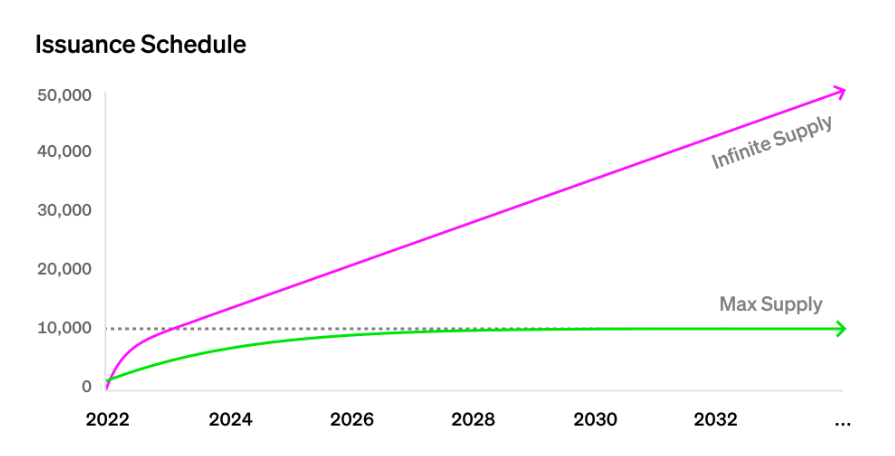
起初，Paradigm計劃較快地發行這兩個NFT。隨著時間的推移，一個以固定的供應量達到頂峰，而另一個則永遠以緩慢的恆定速率發行。 Paradigm力求實現這些目標，同時保持無縫的用戶體驗，讓用戶可以隨時購買NFT，而無需按時等待預定的拍賣。解決方案VRGDA由此應運而生，它是泛化版的GDA，允許用戶在任意時間發行NFT，而不是按照規劃與進度，標準化且線性地進行GDA。
機制
建立直覺
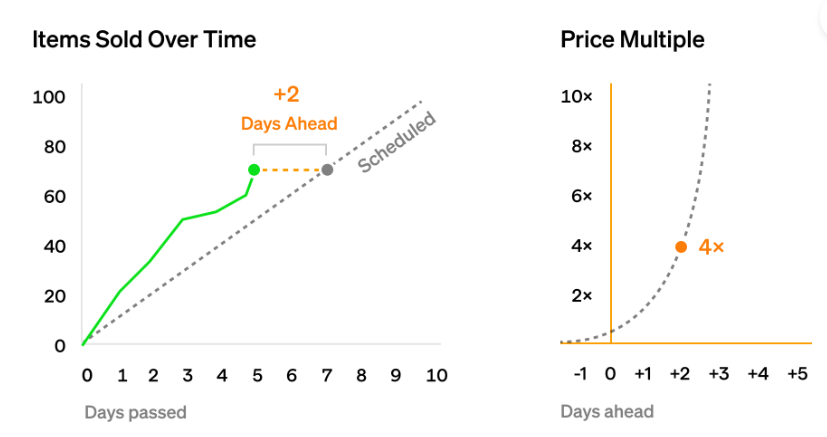
想像這麼一個簡單的計劃表，我們希望每天銷售10個NFT，並為第一個NFT設置了1代幣的起始價格。假設到了第5天，那麼我們應該已經賣出50個NFT。但是由於這幾天市場需求很高，我們早已賣出了70個，本來計劃是7天的銷售量，我們提前兩天完成。故而我們會希望在未來以更高的價格進行售賣。這就需要使用指數曲線來確定究竟應該高多少，這個結果會因參數而異。但在這種情況下，假設我們使用“提前兩天"的參數，因此我們以“2 2 =4”的倍數來提高價格，所以在初始價格是1個代幣的基礎上，新價格將是4個代幣，這使得購買更多NFT變得更加困難。假設又過了10天后，即在第15天時，按計劃本我們應賣出150個NFT，但用戶只購買了120個，這是在第12 天就應該達到的數量，意味著我們落後於計劃三天。所以我們可以將價格調整為原來的2 -3 =0.125倍，方便用戶購買更多的NFT。
建造
參數
P 0 ：按照計劃以完美的進度售出NFT時的售價（即目標價格）。
k：在沒有用戶購買的情況下，NFT價格在單位時間內下降的百分比。
f(t)：表示在t時計劃出售NFT的目標數量。
客觀情況
我們希望按特定時間表發行NFT。我們將使用的機制是，如果NFT出售速度超出預期，則提高價格，如果NFT出售速度相較滯後，則降低價格。如果銷售完全按計劃進行，則保持當前價格不變。
定義
假設我們想按照f(t)描述的時間表出售NFT，該時間表將一個時間點映射到那時我們想要出售的NFT的累積數量。例如，如果我們想每兩天賣出一個NFT，我們會這樣定義：f(t)=t/2
假設我們通過獨立的GDA來售賣每個NFT。如果我們將每個NFT的起始價格設置為1，並讓該價格在沒有銷售的情況下以每單位時間k的速率衰減，則在t時的購買價格將是：(1-k) t
為了給自己實現目標所需的靈活性，我們可以將拍賣的起點在時間上移動至Sn，由此可推導出該NFT在t時刻的價格是：
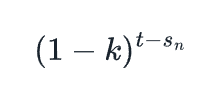
如果我們希望我們的目標價格不同於1，我們可以乘以一個常數p。我們稱之為調整後的價格vrgda n (t)為：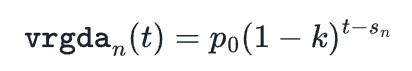 
決定Sn
根據我們的發行時間表f，我們想在t n時賣出第n個NFT。我們可以通過用f來反推t n ，從而得出第n個NFT被出售的具體時間為：tn=f - 1 (n)
VRGDA目標的一個結果是，如果第n個NFT根據其發行時間表在目標時間準確購買，其價格將為P0。正式表達，這意味著如果我們以準確的目標價格出售，那麼在時間t n ，第n個NFT的定價將為：
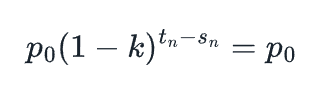
通過除法進行簡化，我們知道以下內容應該始終成立：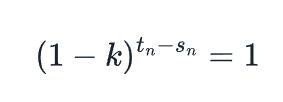 
這意味著t n - S n =0或S n = t n，使用我們上面t n的定義，可得知S n =f - 1 (n)。
最終公式
通過將S n的定義代入vrgdan(t)，我們最終得到最終公式：
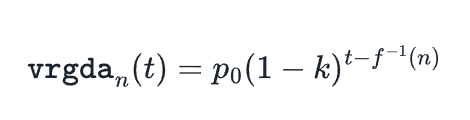
簡單的發行時間表
下面我們演示推導一些簡單的發行時間表以與VRGDA 公式一起使用。
線性
假設我們想每天出售r個NFT。則有f(t)=rt，那麼f - 1 (t)=t/r
將f - 1 (t)代入VRGDA定價公式後，我們得到以下結果：
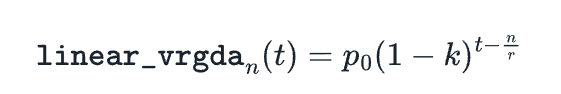
請注意，這與GDA同構，這也是稱VRGDA為GDA的泛化的原因。
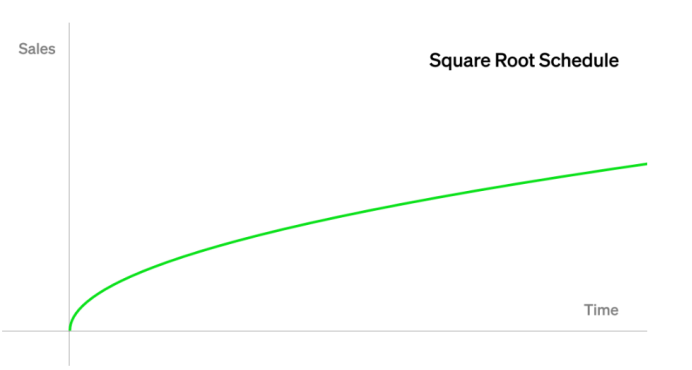
平方根
假設我們希望以與時間的平方根成正比的速率發行NFT。例如，一開始以較快的速度發行NFT，然後隨著時間的推移而變慢，但永遠不會停止。
然後我們可以設置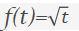
，這樣在第1天我們賣出了1個NFT，在第4天我們賣出了2個，在第9天我們賣出了3個，依此類推。
在這種情況下，f - 1 (n)=n 2 。現在我們只需插入VRGDA定價公式即可獲得：
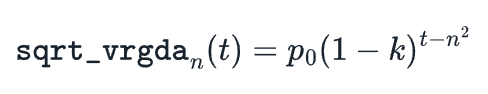
模型發行時間表
與上述示例相比，模型發行計劃有些複雜。然而，我們仍然選擇詳細介紹它，因為它提供了一種在不強制實施無限通貨膨脹機制的情況下引導初始增長的方法。
動機
假設我們一開始想快速發行NFT，然後放慢速度，直到最終發行了某個最大數量，正如Art Gobblers中的情況一樣。
對此進行建模的一種簡潔方法是使用具有正域的邏輯函數。
導出f
邏輯函數是一個S 形曲線。我們將稍微簡化一下並將其定義為：
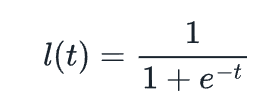
這條曲線在接近負無窮時接近0，在接近無窮大時接近1。
對於我們的特定應用程序，我們不想使用完整的S 曲線（儘管也可能有一個完整的邏輯VRGDA，它會開始緩慢、加速，然後再次減速）。相反，我們只想使用曲線中為正的部分。
因為l(0)=0.5，但是我們希望我們的時間表顯示時間為0時賣出0個NFT，我們需要通過減去0.5來將此函數曲線向下移動。這條新曲線將從0變為0.5：
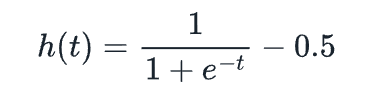我們想要發布L-1個NFT（我們選擇這個是為了記號方便，因為該函數會在到達L之前與之漸近），因此我們需要將該函數乘以2L。
我們還可以引入一個時間尺度參數來調整髮行NFT 的速度：
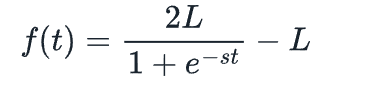
採摘
要選擇s，請注意：
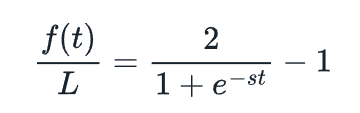此外：
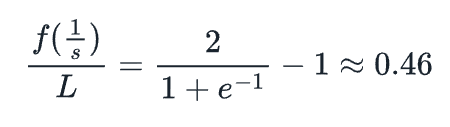這意味著我們可以通過選擇大約期望值的46%的nft發行的時間來選擇s。例如，如果我們希望在100個時間單位後發行46%的NFT，這意味著1/s=100，所以s=1/100。
公式
取上述收益率f(t)的倒數：
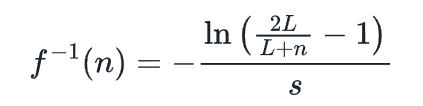
綜上所述，我們最終得到以下公式：
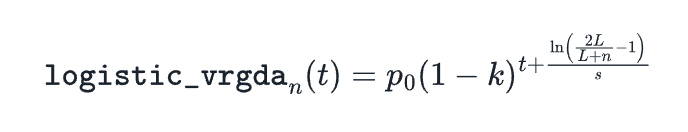
執行
可以在傳輸11/VRGDA 上找到高度優化、生產就緒且獲得許可(MIT) 的VRGDA 實施和各種發行時間表。歡迎使用改進的拉取請求。
結論
VRGDA提供了一種使用幾乎任何您想要的時間表發行NFT的方法，同時仍然允許用戶隨時無縫地購買它們。在Art Gobblers的案例中，它們使我們能夠定制我們的社區增長和UGC動態。以0xMonaco為例，它創造了一個具有挑戰性且競爭激烈的遊戲循環。我們相信它在NFT、鏈上游戲、DeFi等領域還有許多其他潛在應用。
