PART5.Performance and Risk Management
资金管理-本节讨论交易中最基本的概念之一——自由裁量权和算法——即资金管理。天真的投资者/交易员可能认为,唯一重要的投资目标就是尽可能多地赚钱。然而,长期交易的现实更为复杂。由于市场参与者有不同的风险偏好和约束,投资者可能拥有许多目标。
许多散户认为,唯一的目标是不断增加账户净值,而很少或根本不考虑实现这种增长的策略的“风险”。更老练的散户投资者会衡量账户的回撤情况,根据他们的风险偏好,他们或许能够应对账户净值的大幅下降(比如50%)。他们之所以能够应对如此大规模的回撤,是因为他们认识到,从量化上讲,通过使用杠杆,这种行为可能是投资组合长期增长率的最佳选择。
机构投资者可能会从另一个角度考虑风险。机构投资者通常规定了最大回撤额度(比如20%),并对行业配置和日均成交量限制给予了重要考虑。它们将成为资本配置策略“优化问题”的额外约束。这些因素甚至可能比最大化投资组合的长期增长率更重要。
因此,我们可以在通过杠杆使长期增长率最大化和通过限制回撤的持续时间和幅度使“风险”最小化之间取得平衡。帮助我们实现这一目标的主要工具叫做凯利准则。
凯利准则-在这一部分,凯利标准将是我们的工具,以控制杠杆,并分配到一套算法交易策略,组成一个多策略的投资组合。
我们将把杠杆定义为一个投资组合的规模与该投资组合中实际账户净值的比率。为了更清楚地说明这一点,我们可以用抵押贷款买房来做类比。你的首付款构成了你的帐户净值,而首付款加上抵押贷款价值构成了相当于一个投资组合的规模。因此,一套20万美元的房子(抵押贷款15万美元)首付5万美元就构成了(15万+ 5万)/5万= 4的杠杆。因此,在这种情况下,你在房子上的杠杆是4倍。保证金账户的投资组合表现类似。有一个“现金”组成部分,然后更多的股票可以通过保证金贷款来提供杠杆作用。
在我们陈述凯利准则之前,我想特别概括一下推导过程中的假设,这些假设有不同程度的准确性:
● 每个算法交易策略将被假定拥有一个正态分布的回报流(即高斯)。此外,每种策略都有其固定的收益均值和标准差。该公式假设这些平均值和std值不变,即它们在过去和将来是相同的。这显然不是大多数策略的情况,所以要注意这个假设。
● 这里考虑的回报是超额回报,这意味着它们扣除了所有融资成本,如保证金利息和交易成本。如果该策略是在机构环境下实施的,这也意味着回报是扣除管理和绩效费后的净额。
● 所有的交易利润都进行了再投资,没有提取净值。这显然不适用于扣除上述管理费、投资者经常撤资的机构。
● 所有的策略在统计上都是独立的(策略之间不存在相关性),因此策略收益之间的协方差矩阵是对角的。
现在我们来看看实际的凯利准则,假设我们有一组N种算法交易策略,我们希望确定如何为每种策略应用最优杠杆以使增长率最大化(但将回撤降至最低),以及如何在每种策略之间分配资本。如果我们将每个策略i之间的分配表示为长度为N的向量f,使得 ,则每个策略
最优分配的Kelly准则为:
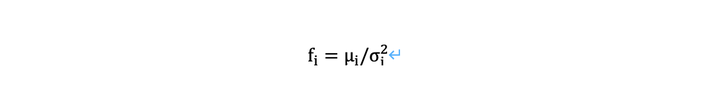
策略i中 为平均超额收益和
为超额收益的标准差。这个公式基本上描述了最优杠杆应该应用于每个策略。
虽然Kelly准则给出了最优的杠杆率和策略配置,但我们仍然需要实际计算出投资组合的预期长期复合增长率,我们用g表示,其公式为:
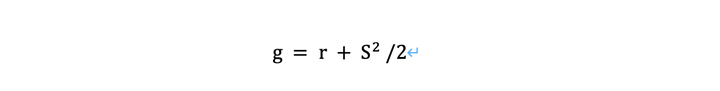
其中r是无风险利率,也就是你可以从经纪人那里借钱的利率,S是策略的年度夏普比率。后者是通过年度平均超额回报率除以年度超额回报率标准差计算出来的。有关夏普比率的详情,请参阅前一章有关业绩衡量的内容。
一个现实的例子-让我们考虑一个例子在单一策略情况下(i = 1)。假设我们做多一个神话般的XYZ股票平均年回报率m = 10.7%,年度标准差σ= 12.4%。此外,假设我们能够以无风险利率r = 3.0%借款。这意味着平均超额收益是µ = m − r = 10.7 − 3.0 = 7.7%。这给出了S = 0.077/0.124 = 0.62的夏普比率。
这个我们可以计算最优凯利杠杆通过 = 0.077/0.1242 = 5.01。因此Kelly杠杆说,对于一个10万美元的投资组合,我们应该额外借入40.1万美元,使总投资组合价值为501,000美元。在实践中,我们的经纪公司不太可能让我们有这么大的保证金交易,所以凯利标准将需要调整。
我们可以用夏普比率S和利率r来计算长期复合增长率g。 == 0.22,即22%。因此,我们应该期待这一策略每年22%的回报。
更多内容请关注公众号【火象】~















