PART5.Performance and Risk Management
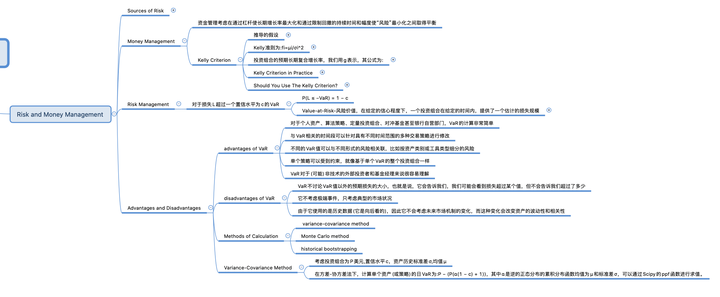
优势和缺陷
VaR在金融行业中非常普遍,因此您应该熟悉这种技术的优点和缺点。VaR的一些优势如下:
● 对于个人资产、算法策略、定量投资组合、对冲基金甚至银行自营部门,VaR的计算非常简单。
● 与VaR相关的时间段可以针对具有不同时间范围的多种交易策略进行修改
● 不同的VaR值可以与不同形式的风险相关联,比如按资产类别或工具类型细分的风险。例如,这使得我们很容易解释投资组合风险集中在哪里。
● 单个策略可以受到约束,就像基于单个VaR的整个投资组合一样。
● VaR对于(可能)非技术的外部投资者和基金经理来说很容易理解。
然而,VaR也并非没有缺点:
● VaR不讨论VaR值以外的预期损失的大小,也就是说,它会告诉我们,我们可能会看到损失超过某个值,但不会告诉我们超过了多少。
● 它不考虑极端事件,只考虑典型的市场状况。
● 由于它使用的是历史数据(它是向后看的),因此它不会考虑未来市场机制的变化,而这种变化会改变资产的波动性和相关性。
VaR不应该单独使用。它应该始终与一套风险管理技术一起使用,例如多样化、最佳投资组合配置和谨慎使用杠杆。
计算方法-到目前为止,我们还没有讨论实际计算的VaR,无论是在一般情况下或一个具体的交易例子。我们会对三种技术感兴趣。第一种是方差-协方差法(使用正态性假设),第二种是蒙特卡罗方法(基于潜在的非正态分布),第三种是历史自举法,它利用历史收益信息来评估资产。
在这一节中,我们将集中讨论方差-协方差法。
方差-协方差法-考虑一个投资组合为P美元,置信水平c。我们正在考虑日常的回报,与资产(或策略)历史标准差σ,均值为µ。然后,在方差-协方差法下,计算单个资产(或策略)的日VaR为:
P − (P(α(1 − c) + 1))
其中α是逆的正态分布的累积分布函数均值为µ和标准差σ。
我们可以使用SciPy和pandas库来计算这些值。如果我们设置P = 106和c = 0.99,我们可以使用SciPy的 ppf方法生成逆累积分布函数值,且服从均值为µ方差为σ的正态分布,从而获得一些在这种情况下,花旗集团的历史每日回报的真正的财务数据(我们很容易代入算法策略的回报):
#!/usr/bin/python
# -*- coding: utf-8 -*-
# var.py
from __future__ import print_function
import datetime
import numpy as np
import pandas.io.data as web
from scipy.stats import norm
def var_cov_var(P, c, mu, sigma):
"""
方差-每日风险值的协方差计算
使用置信水平c,均值为mu
投资组合的标准差sigma
价值P
"""
alpha = norm.ppf(1-c, mu, sigma)
return P - P*(alpha*(1-c) + 1)
if __name__ == "__main__":
start = datetime.datetime(2010, 1, 1)
end = datetime.datetime(2014, 1, 1)
citi = web.DataReader("C", ’yahoo’, start, end)
citi["rets"] = citi["Adj Close"].pct_change()
P = 1e6 # 1,000,000美元
c = 0.99 # 99%置信区间
mu = np.mean(citi["rets"])
sigma = np.std(citi["rets"])
var = var_cov_var(P, c, mu, sigma)
print("Value-at-Risk: $%0.2f" % var)风险价值的输出为:
Value-at-Risk: $56503.12风险价值在所有领域的财务管理中是一种非常有用和普遍的技术,但它不是没有缺点。著名对冲基金经理戴维•艾因霍恩(David Einhorn)曾将风险价值描述为“一个安全气囊,除了发生车祸的时候,它一直都能工作”。实际上,你应该始终使用VaR作为风险管理覆盖的一个补充,而不是一个单一的指标!
更多内容请关注公众号【火象】~

















