本期万向区块链小课堂将为大家讲解区块链中经常提及的一棵树:默克尔树(Merkle Tree)。
来回忆下我们之前小课堂解构的区块链六层模型,默克尔树封装在数据层,说明它是一个密码学技术,用以保护区块链的安全。

默克尔树于1979年由美国计算机科学家拉尔夫·默克尔(Ralph Merkle)提出,本质上是一种树状数据结构,由数据块、叶子节点、中间节点和根节点组成。所以,一组合,就叫“Merkle Tree”。
默克尔树各部分的构成关系如下图:
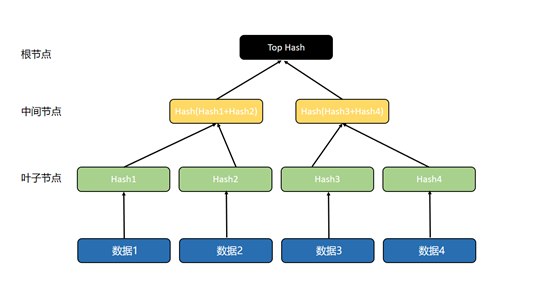
要得到这样一棵默克尔树,首先要对底部数据块进行哈希运算,用每个数据块对应的哈希值生成叶子节点。再对相邻的2个叶子节点进行哈希运算,得到的哈希值生成中间节点,最后对相邻的2个中间节点进行哈希运算,得到的哈希值生成根节点。由于各类节点都是由哈希值构成,因此默克尔树又被称为哈希树,即储存哈希值的树状数据结构。
看起来是不是很像一棵底下堆满了礼物的圣诞树?

哈希运算和哈希值
生成默克尔树用到的哈希运算是区块链中常用的加密函数。任意大小、长度的数据经过哈希运算后都会得到一个固定大小和长度的数值,即哈希值。就像我们的指纹或签名能帮助鉴别我们的身份,哈希值也可以看成是数据的指纹或签名,用于验证数据的真实准确性,并具有以下特征:
确定性
数据和哈希值之间是确定的一一对应关系,即相同数据经过哈希运算会得到相同的哈希值。
不可逆性
哈希运算的过程是不可逆的,即数据经过哈希运算可以得到哈希值,但不可以通过哈希值推导出原始运算数据,由此保证数据的隐私和安全性。比如Facebook等网站会将用户密码计算成哈希值并储存。用户每次输入密码时,密码都会被转换成哈希值与网站记录的版本进行对比,从而验证密码是否正确。由于哈希运算的不可逆性,网站无法从哈希值中推导出用户密码,从而保证用户信息安全。
统一性
即上文提到的任意大小、长度的数据经过哈希运算后会生成大小、长度统一的哈希值,一方面起到压缩数据,减轻数据储存压力的作用,另一方面规整了杂乱无章的原数据,方便后期比对验证。
为什么要用默克尔树?
由于默克尔树本质上是由哈希值构成的树状数据结构,因此也继承了哈希值用于保证数据安全隐私和校验数据准确和完整性的功能,主要应用于点对点下载,例如BT下载、开源分布式控制系统Git、比特币和以太坊区块链等场景中。因为我们难以保证这些去中心化系统中的每个节点都会提供真实可信的数据,也难以避免数据在传输过程中出现丢失、损坏等情况,所以需要引入数据加密和校验机制。
看到这里,你可能已经意识到了默克尔树其实就是将数据分割成多个小块,进行多次哈希运算,搭建出的一个树状数据结构。那为什么要对数据进行拆分,计算出多个哈希值用于校验呢?这不是增加工作量了吗?但其实这样做是为了提高数据验证的灵活性,数据量越大,默克尔树的这一优势会体现得越明显。
试想一下,如果我们不对数据进行拆分,而是将整体计算成一个哈希值,那当数据校验出现问题时,我们很难分辨问题出现在哪里,只能回过头去对整个数据进行排查,如果数据量特别大,那么这个错误排查过程无异于海底捞针。
但在默克尔树里,数据被拆分成多个小块,形成了多个分支,可以根据具体情况对部分数据进行校验,无需校验整个数据,从而提高数据校验的灵活性和效率。
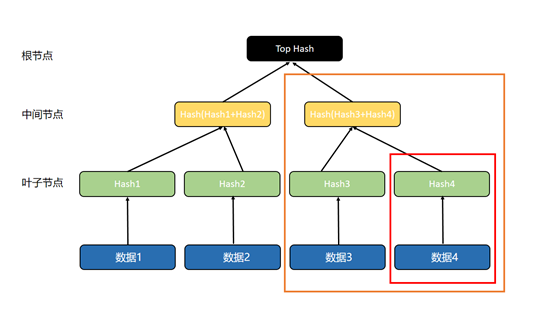
最后总结一下默克尔树的知识要点:
- 由哈希值构成的树状数据结构
- 用于验证验证区块链等去中心化系统中的数据的完整准确性
- 具有灵活高效验证数据的优势














