
作者:Gerry Wang
来源:Arweave Oasis
详情请访问原文链接。
本文有些硬核,因为会有很多数学推导论证过程,各位朋友要作好准备。但笔者认为数学作为基础学科,在从逻辑上解释一个事物有着极强的精准性,所以不妨让笔者试试用简单的语言来展示 @ArweaveEco 机制中的数学之美。
在白皮书解读(二)文章中,我们描述了简洁访问证明( #SPoA )游戏可以被任何参与者用来证明他们在数据集的特定位置确实存储了一些数据。这个模式还可以用来创建第二个游戏,我们称其为简洁的复制证明(Succinct Proofs of Replications #SPoRes ),这将允许证明者无论数据集大小如何,都能以极小的数据传输和验证成本,来向验证者证明自己存储了一定数量的数据副本。
SPoRes 游戏
简洁的复制证明(SPoRes)游戏是这样进行的。Alice 声称她存储了 n 份默克尔化数据集的唯一副本。Bob 想要验证 Alice 有没有说谎。为了做到这一点,他给 Alice 一个难度参数 d 和一个随机产生的种子 Seed。Alice 使用这个 Seed 生成一个每秒钟发出一个检查点的 VDF 哈希链,这个检查点可以用来解锁数据集内最多 k 个 SPoA 挑战。每当她有对应于这些挑战的打包数据块时,Alice 可以构建相应的 SPoA 证明。然后将这些证明进行哈希处理,并与 Bob 的难度参数 d 进行对比。如果证明哈希值大于 d,则 Alice 找到了一个有效解决方案,并将相应的证明发送给 Bob。Bob 则记录下发送随机种子到收到 Alice 有效证明之间的时间。
基于难度 d,单次尝试找到有效解决方案的概率 p 的表达式为:
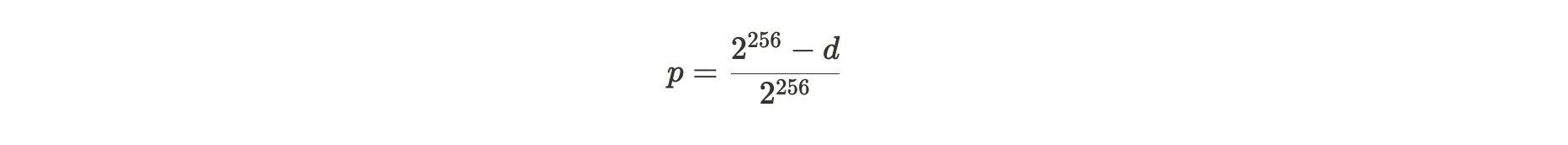
公式注解:由于基于 SHA 256 的算法是一个 256 位字符串,所以就有 2^256 ( 这里「^」表示的是次方的意思 ) 个最大哈希数量,如果要找到大于 d 的有效解决方案,那只有 2^256-d 个哈希数量,以此可以计算出单次尝试成功的概率。
如果 Alice 有 n 个副本,并且每秒每个副本可以进行 k 次尝试,那么她在任何给定的一秒时间内找到解决方案的概率是:
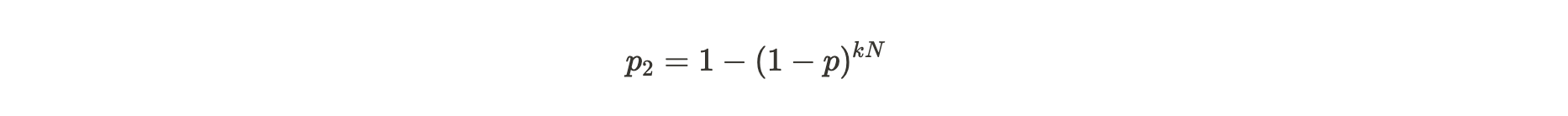
公式注解:kN 的意思为 Alice 在一秒内总共可以进行的哈希解决方案尝试次数,这个尝试次数与 Alice 存储的唯一副本数量成正比,具体解释可以阅读此前文章 《Arweave 2.6 也许更符合中本聪的愿景》的内容。1-p 是单次尝试失败的概率。p2 的概率值就是 1 减去 kN 次尝试失败的概率的差。
通过上述两个公式的代入推导,我们可以得到:
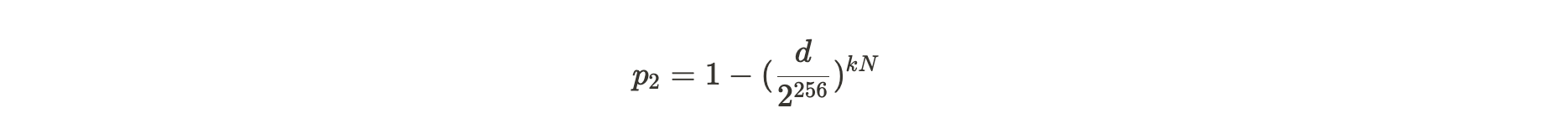
公式注解:将 p 代入至 P2 的公式中所得结果
Alice 提交证明所需的时间可以用一个几何随机变量 X ~ geom(p2) 来模拟,p2 为成功的概率。这个随机变量 X 取决于 d,k 和 n。为了验证 Alice 是否说谎,Bob 发送一个难度 d,使 Alice 以有 n 个副本的前提下,可以每 120 秒向 Bob 提交一次证明。这相当于 Alice 在 120 秒的成功概率为:
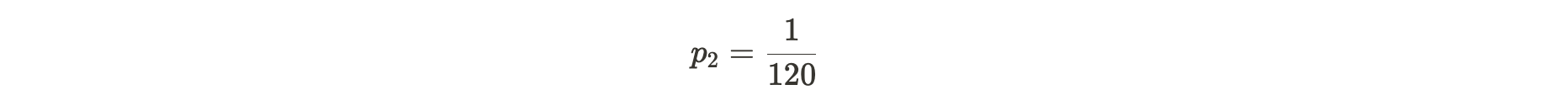
公式注解:1/120 为 120 秒内成功提交一次证明的概率
如果 Alice 可以在要求的时间内提交证明,那她很可能拥有正确数量的唯一副本。但一次证明是不足以让 Bob 确信 Alice 没有说谎,如果 Alice 能在很长一段时间内平均每 120 秒一直提交证明,Bob 才可以合理地确信 Alice 存储了符合期望的数据量。
接下来我们尝试去量化 Bob 对 Alice 存储的确定性。
假设 Alice 声称存储了 20 个副本,并且在 2 周的时间内以平均 120 秒的速度一致地提交了证明(总共提交了 10,080 个证明)。此时,Bob 在想如果 Alice 只存储了 19 个(或更少)的副本,她依然能提交这些证明的概率是多少。这对应于在不同的一秒钟内提供证明的概率:
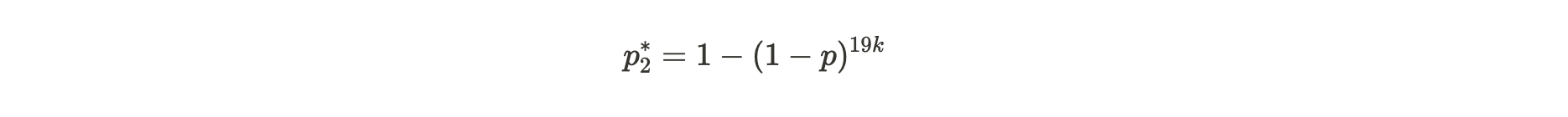
公式注解:这里出现的 19k,就是 Alice 存了 19 个副本,每个副本拥有 k 次尝试寻找解决方案的次数。
过简化:
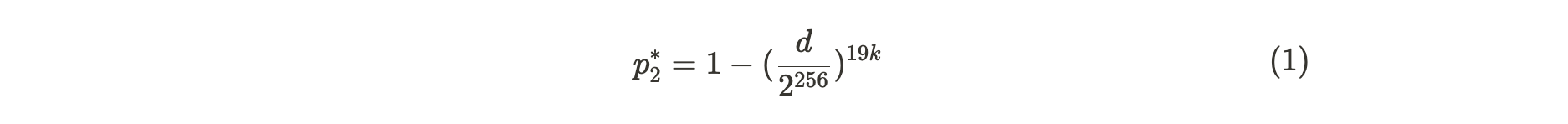
这个概率可以使用 Bob 为诚实的 Alice 生成的 d 值来计算。如果她存储了 19 个或更少的副本,她一秒钟内提供证明的概率可以通过下面给出的一系列推导得到。其中, p2 代表了 Alice 诚实存储了 20 个副本时,一秒内生成证明的概率,而 p2* 则代表如果她在说谎(存储≤ 19 个副本)时,一秒内提供证明的概率:
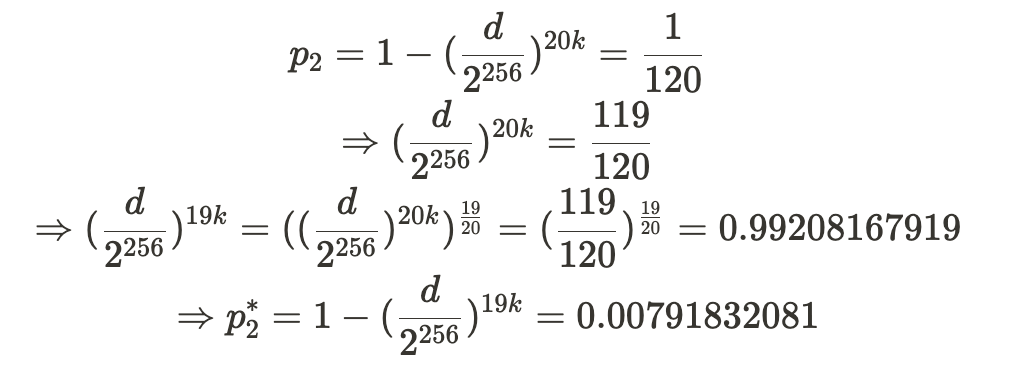
这个推导过程看似很复杂,其实有基础数学能力的朋友就都能看懂。推导过程就是上述公司的代入过程。
因此,p2*=0.00791832081,对应于预期的证明生成时间为 126.2894 秒。设 X* 为从 p2* 得到的 Alice 提交证明的时间,即 X*~ geom(p2*) 。这代表了 Alice 在说谎情况下 —— 只存储了 19 个副本,所花去的提交证明的时间 X* 的期望值(平均值)是:
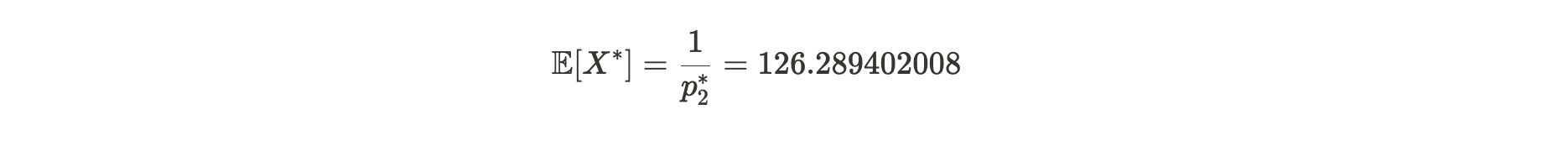
公式注解:E[X*] 表示 Alice 在只存储了 19 个副本的前提下,成功提交证明的平均时间在 126.2894 秒。而如果她存储了 20 个副本,成功提交时间则平均在 120 秒。
我们可以使用中心极限定理来估算样本均值低于 120 的概率,即与上述得到的期望值 E[X*] 不同。这个概率表示为:
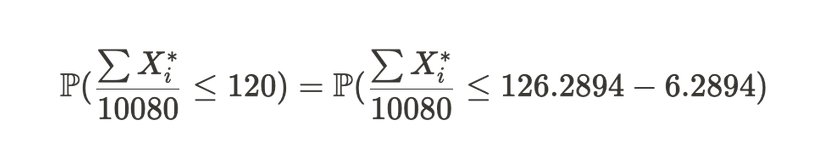
公式注解:等式左边表达式代表在两周时间内,Alice 平均每次提交证明的时间小于等于 120 秒的概率。等式右边则是左边表达式的变体。
对于大量样本来说,这个不等式左侧趋向于一个均值为 E[X*] 和方差为 σX*^2/n 的正态分布,其中 σX* 是 Xd 的标准差,n ( 这里 =10,080) 是样本大小。因此,上述公式可以变为:
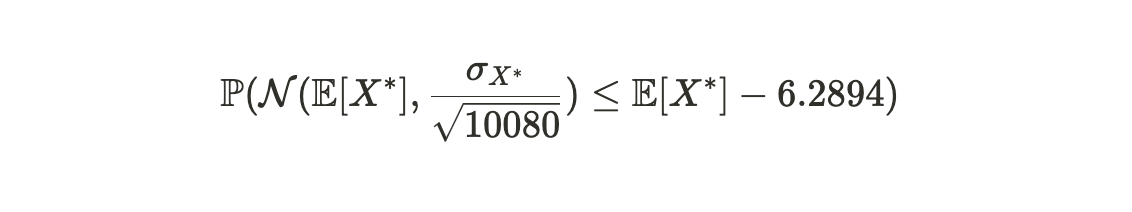
我们可以将这个分布转换为标准正态形式,以获得等价的概率:
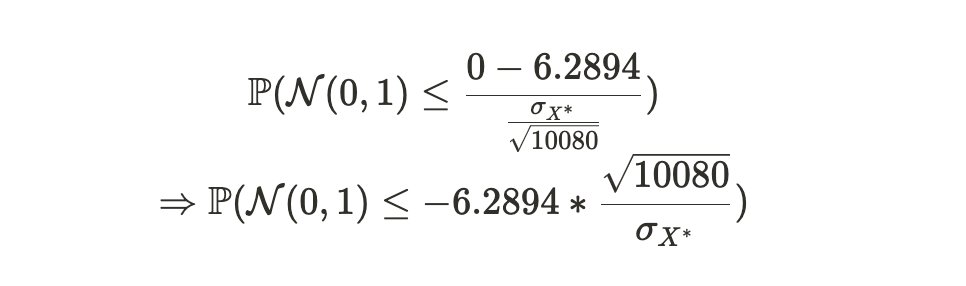
最终,使用标准正态分布表,我们可以获得 Alice 在这周时间周期中说谎的概率:
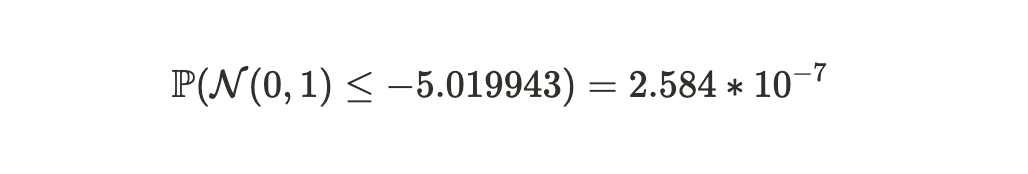
因此,在这个例子中,Bob 可以以约 99.99997416% 的确定性判断,在这 2 周时间里 Alice 存储了超过 19 份数据集的副本。我们注意到,如果 Alice 存储的副本少于 19 份,预期的证明提交时间将大于 126.3 秒。我们还注意到,整个证明系统仅需要每 120 秒传输一次证明。这是 Alice 和 Bob 之间的平均数据传输率为每秒 2.389 KB(280 KB/120 秒),与比特币网络的同步开销相当。
最后,这些概率不会随着数据集大小的任意增加而改变,而增加采样周期将以超线性的速率持续提高 Bob 对 Alice 副本数量的确定性的准确度(图 1)。
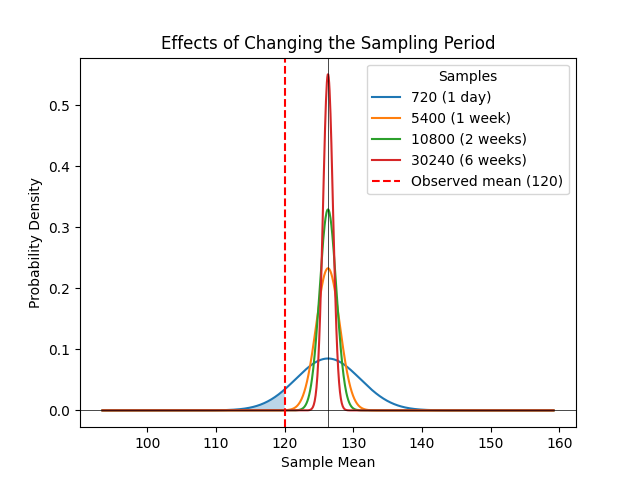
图 1:在简洁复制证明(SPoRes)游戏中,确定性相对于样本持续时间的增加是超线性的。经过两周的样本收集,维持少于 19 个副本的概率是微不足道的(P<0.0000002584)。
所以,一个 SPoRes 游戏由以下参数定义:
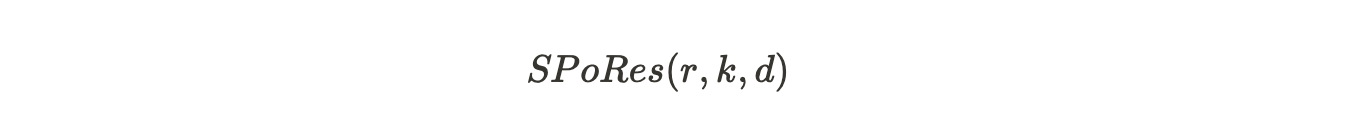
其中:
r= 用于游戏的数据集的默克尔根。
k= 每个副本每秒钟解锁的最大的挑战数量。
d= 决定每次尝试时的成功概率的难度参数。
通过这些有趣的数学推导,我们可以放心地确定,只要在一个合理的时间段中让矿工持续提交证明就能确定数据是否被储存。这构成了 Arweave 以去中心化存储为目标的共识机制的核心。数学的乐趣才刚刚开始,接下来的文章中还会有更多有趣的推演与论证。











