撰文 :Leo Zhang、Jack Koehler、Karim Helmy ;前两者就职于算力及衍生产品研究机构 Anicca Research,后者是 Coin Metrics 数据研究分析师
本文是《明智的比特币矿工》系列第二篇,上一篇为《明智的比特币矿工,应当像管理投资一样运营算力》,由 Anicca Research 与新加坡算力及衍生产品投资和交易机构 General Mining Research (GMR)合作撰写。
「当然,任何试图用确定性的方法产生随机数的人,都生活在罪恶中。」约翰·冯·诺伊曼 (John von Neumann)
概述
在难以通过实验检验假设时,可以通过模型模拟收益变化。比特币挖矿业不透明,资本密集度高,但如果以数值模拟为主,定性分析为辅,研究该行业时会更加简单易行。在无法判定市场变化的前提下贸然投资挖矿的代价是昂贵的,但在实际操作之前建立模型却很便宜。
在本系列的第一部分中,我们建立了蒙特卡罗模型来模拟矿机的公允价值以及该公允价值对不同市场参数的敏感性。我们证明了:由于矿机流动性较差,算力的市场价格经常偏离其理论公允价值。
参考阅读:
《明智的比特币矿工,应当像管理投资一样运营算力》
在上一篇文章中,我们用跳跃扩散 (Jump-Diffusion) 过程对未来的价格轨迹进行了建模,并使用线性函数来描述全球算力如何响应价格的变化。但正如我们的几篇文章中所讨论的那样,算力和价格之间的动态关系超出了简单的线性关系。为了提高我们框架的代表性,我们必须将全网算力作为一个单位的方法提高精度,从自下而上的角度来建模。
参考阅读:
《Bitcoin Mining’s Three Body Problem》
https://www.aniccaresearch.tech/blog/bitcoin-minings-three-body-problem
在本文中,我们根据矿机类型、全部运营成本和挖矿策略,将矿机定性为几种原型。每个矿工原型都有着不同的利润率和风险考量。随着挖矿收入发生波动,每个矿工会产生利润或亏损,而利润或亏损又会促使他们决定增加或减少作业矿机的数量。
在这个框架下,网络算力的变化不仅是价格变化的函数,而且是具有不同经济和风险特征的所有矿工输出的决策的总和。
该模型的代码库是完全开源的,可以在这里(https://github.com/khelmy/intelligent-bitcoin-miner) 获得。
用户可以插入自己的假设,并查看他们的挖矿业务在此后的表现。在本文中,我们将详细介绍该模型,解释如何使用该模型,并从五个场景的分析中给出一些有趣的发现。
康威的生命游戏
我们将网络算力建模为单个矿工输出的总和,这种方法是基于一种叫做基于代理的模拟技术。基于代理的建模起源于 20 世纪 50 年代约翰·冯·诺伊曼 (John Von Neumann) 关于细胞自动机的早期研究,并因约翰·康威(John Conway)的《生命游戏》而流行起来。

图片来源: Teb’s Lab
参考阅读:
《Agent-based modeling》
https://en.wikipedia.org/wiki/Agent-based_model
《How I optimized Conway’s Game Of Life》
https://medium.com/tebs-lab/optimizing-conways-game-of-life-12f1b7f2f54c
《Play John Conway’s Game of Life》
https://playgameoflife.com/
这是一个回合制的模拟,发生在一个二维的细胞网格上。一个预先指定的、决定性的规则负责管理相邻细胞之间的相互作用。每一个回合,细胞的状态都会根据其相邻细胞的状态而改变:如果细胞刚好有三个活着的邻居,它们就会复活;如果有两个或三个活的邻居,它们可以存活,否则则会死亡。
《生命游戏》是基于代理的模型的一个原始例子,这是一种由共享全局状态的参与者做出决策的模拟类型。在《生命游戏》中,细胞是代理人,它们的决策围绕着生存还是死亡展开。结果完全取决于棋盘的初始状态,而棋盘的状态可能会以非直观的方式演变。
基于代理的建模已经较康威的《生命游戏》有了很大的发展。如今,基于代理的模拟被广泛应用于生态学、经济学、量化金融和智能合约分析。
参考阅读:
《Insights from the study of complex systems for the ecology and evolution of animal populations 》
https://academic.oup.com/cz/article/66/1/1/5477426
比特币挖矿的盈利能力取决于比特币的价格、网络总算力,在较小程度也跟交易费用有关(到目前为止)。计算盈利能力的第二个因素,即网络算力,取决于其他矿工打算运行还是关闭机器。因此,对矿工盈利能力的预测必须是迭代的,而这个问题非常适合基于代理的建模。
假设比特币价格完全独立于网络算力,我们可以将价格建模为一个独立的几何布朗运动。可以将时间序列中的每一天视为一个轮次;在每个轮次开始时,价格和全局算力都被输入到矿工代理的决策过程中。
参考阅读:
《Geometric Brownian motion》
https://en.wikipedia.org/wiki/Geometric_Brownian_motion
根据他们的利润率,每个矿工通过改变他们运行的机器数量来扩大或缩小他们的运作规模,并公布他们运作的算力。每个矿工的算力输出之和因此成为新的全局算力。
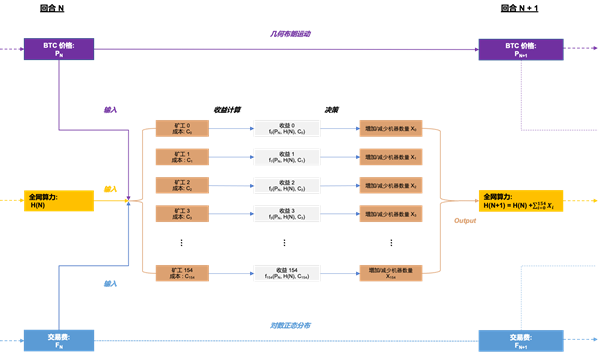
矿工作为代理
将矿工作为代理建模,本质上是对挖矿经济学中的输入变量进行参数化。在《算力的炼金术》 (The Alchemy of Hashpower) 中,我们提出了算力的反身性这个概念:每一个挖矿作业都会受到物理条件和操作者对市场主观感知的严重影响。
参考阅读:
《The Alchemy of Hashpower》
https://www.aniccaresearch.tech/blog/the-alchemy-of-hashpower-part-i
虽然不可能涵盖所有决策因素,但我们认为矿机类型、成本基础和策略应该是决定矿工行为的主要因素。我们在矿工类别中,将这些因素定为了参数。
机器类型
在现实世界中,一个挖矿作业通常涉及多种不同类型的矿机。为了简单起见,我们让每个矿工原型在整个分析过程中使用单一的矿机类型。在这个版本的模拟中,我们支持以下的矿机类型:
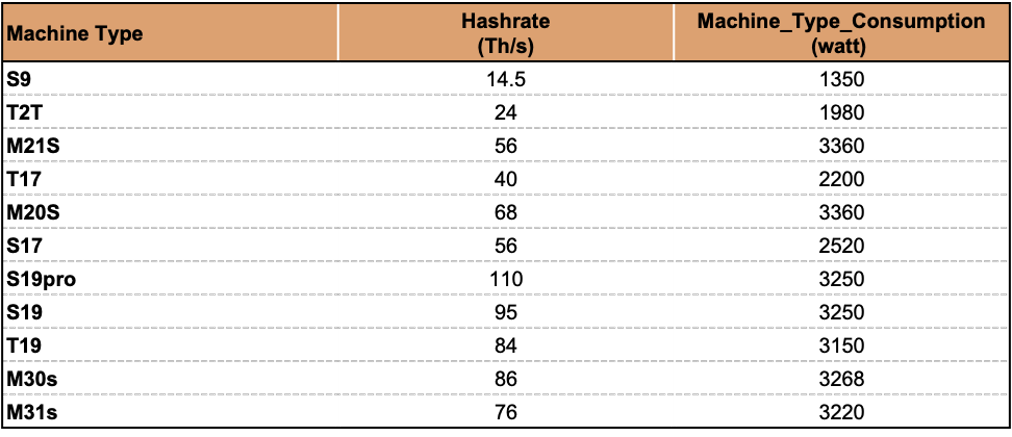
成本基础:总电费能源消耗
在整个模拟过程中,每个矿工都被分配了一个平均的总电量。能量消耗为矿工的:矿机数量*矿机类型消耗。
每天,矿工产生的运营费用等于:能耗 / 1000 *总电费* 24。
我们还指定了一个总电费分布,它决定了初始化时相关矿工原型的矿机数量。
在这个版本中,我们提供以下默认分层。用户可以在运行模拟之前对其进行自定义。
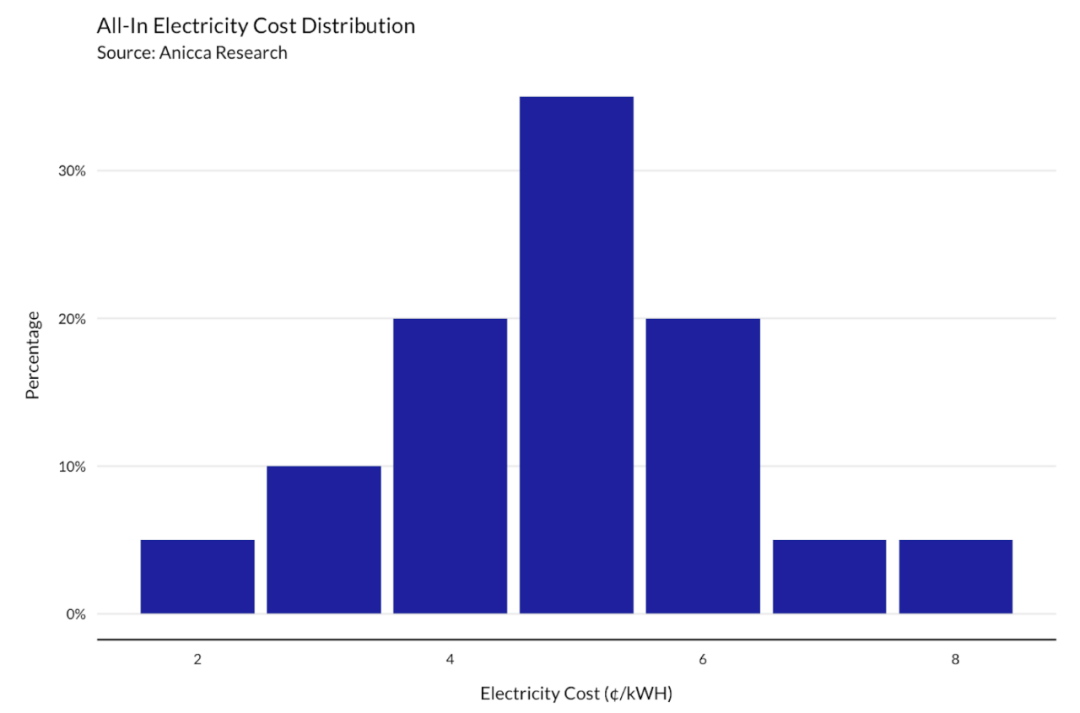
基于最佳努力预测策略
做多比特币
每日出清
每个矿工在初始化时都被分配了一个策略。在实践中,矿工可以使用的策略范围很广,只要他们对市场条件的看法发生变化,就可以在这些策略之间进行切换。
为简单起见,我们在整个模拟过程中按照相同的策略对每个矿工进行建模。在《 智能比特币矿工,第一部分》 (The Intelligent Bitcoin Miner, Part I) 中,我们介绍了这两种策略,并评估了它们在不同市场周期中的表现。
参考阅读:
《明智的比特币矿工,应当像管理投资一样运营算力》
做多比特币意味着矿工每天只卖出足够支付运营费用的比特币,并将其余收入保留在比特币中。
每日出清是指矿工立即将所有资产兑换成美元。
矿工的策略决定了他们的美元仓位和比特币仓位如何划拨。当使用看多比特币策略计算矿工的利润时,需要考虑未实现收益。未实现收益按比特币仓位*比特币价格计算。
基于这三个变量的组合,我们将矿工的世界分解为 11 种矿机类型、7 种电费成本层和 2 种策略,总共 154 种原型。
在初始化时,我们根据 Hashrate Index 和 General Mining Research 以及其他一些来源的数据,提供了市场上矿机的默认分层和价格数据。用户可以在模拟之前自定义:
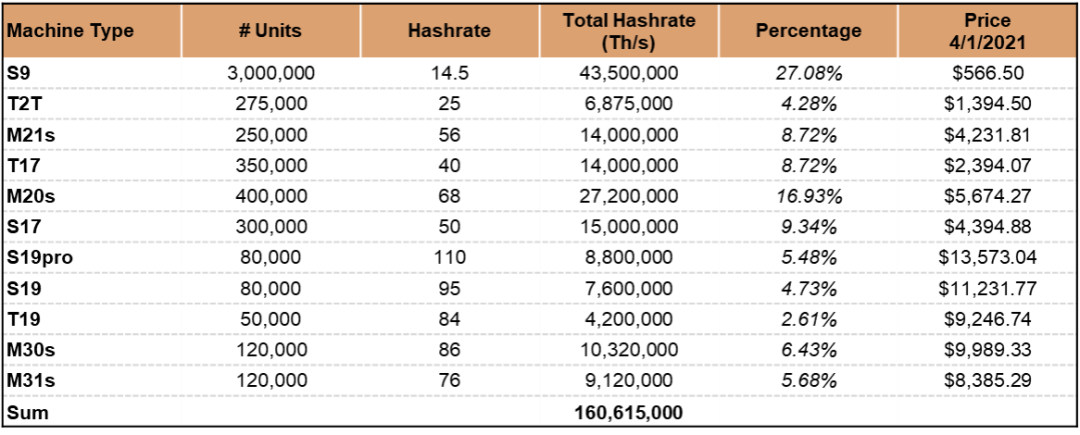
价格数据:Hashrate Index, General Mining Research。算力百分比:基于各种来源的估算
参考阅读:
《Bitcoin runs on Hashrate》
https://hashrateindex.com/
https://www.gmr.xyz/
电费分布和矿机分层是每个矿工矿机数量的输入。这代表了矿工作业的矿机数量。需要注意的是,在实践中,这两个分布并不像模型中假设的那样在统计上是独立的—例如,像 S9 这样的老矿机更有可能是由能够获得更便宜电力的矿工操作。
在模拟开始时,所有矿工的矿机数量*算力的总和被缩放为大致等于当前网络算力水平,这个数值是从 Coin Metrics 中收集的。
参考阅读:
https://charts.coinmetrics.io/network-data/
为了跟踪矿工的表现,我们在矿工类别中加入了一个简单的账户余额和历史利润计算器。
账户余额
美元仓位比特币仓位算力仓位
初始算力仓位为矿工的矿机数*矿机_类型_算力。
盈利能力
每日盈利 最近30天盈利 全部盈利
随着市场的发展,盈利能力决定了矿工的行为。我们将在下一节中介绍该机制。最近30天盈利和全部盈利是延伸盈利的总和。
下面是一个示例矿工类的所有数据条目。矿工类的代码可以在 agents.py 文件中找到。 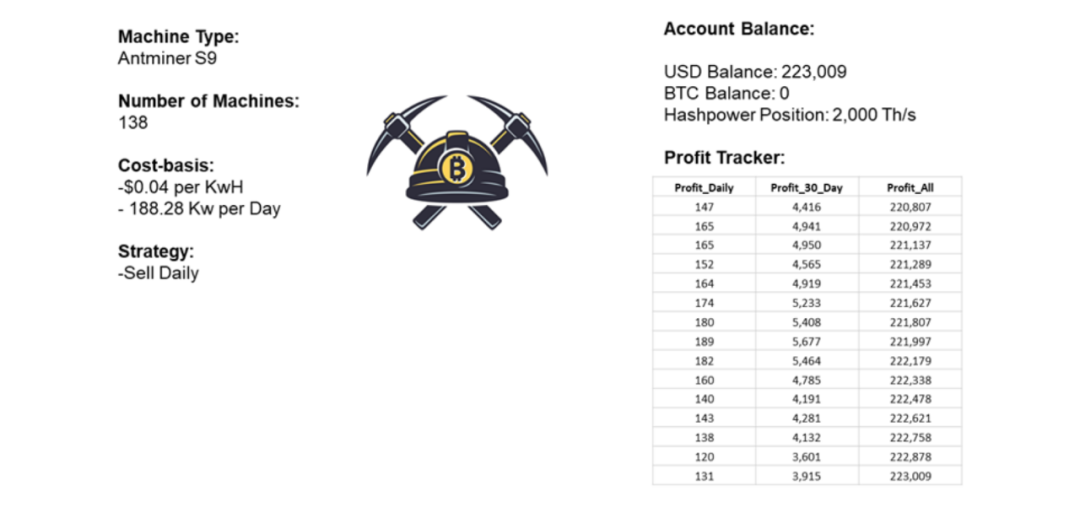
参考阅读:
https://github.com/khelmy/intelligent-bitcoin-miner/blob/main/agents.py
矿工的效用函数
当预期盈利能力较高时,矿工可能会想要购买更多的矿机,当预期未来盈利能力为负时,他们可能会关闭一些矿机以减少运营费用。我们需要准确定义矿工如何增加或减少他们的算力。
在现实中,还会有许多外部因素驱使矿工决定购买或关闭矿机,比如是不是能从外部融资,甚至于他们是不是太累了。为了简单起见,我们将矿工的历史利润作为矿工决策过程中的主要输入进行建模。
决策流程将最近30天盈利作为输入,并计算用于生成操作的结果。计算过程如下:
如果最近30天盈利为零或负数,矿工将矿机数量减少 x,直到盈亏平衡。计算方法很简单:损失(最近30天盈利)除以每台矿机的能耗成本。
如果最近30天盈利为正并超过某个阈值,矿工将增加矿机数量。阈值为:最近30天盈利 > 所有 (支出) 的总和。
增加的矿机数量计算如下:(最近30天盈利所有 (支出) 的总和) / 矿机价格*矿机增长系数。
每种矿机类型都有一个增长率,反映的是它的相对增长。由于制造商缺乏继续生产的意愿,老一代的矿机增长率较小。我们还为添加新矿机设置了一个反应延迟。新订单的生产和交付通常需要一段时间。
在我们的模型中,这意味着在增加 x 台矿机的动作被触发后,矿机不会立即被添加到矿工的账户中。我们设置了一个常量列表作为每种机器类型的反应时间。反应延迟是一个静态近似值,应定期更新,以反映供应链能力的变化。

基于最佳努力估计
总而言之,触发函数会输出矿工买入或卖出的矿机数量。
用户可以用他们认为合适的常量来更新增长因子和反应天数。调整的代码可以在 Simulator.py 中找到。
参考阅读:
https://github.com/khelmy/intelligent-bitcoin-miner/blob/main/Simulator.py
设置模拟
与《第一部分》一样,我们使用一个随机过程来预测比特币在模拟生命周期内的价格。几何布朗运动模型的基础支持来自于从 Coin Metrics 中提取的历史价格数据。
将所有内容结合在一起,我们使用下面的图表来说明这个过程是如何运作的:
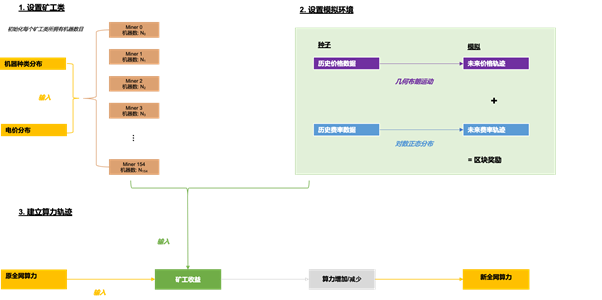
参考阅读:
《明智的比特币矿工,应当像管理投资一样运营算力》
场景分析
为了测试该模型,我们模拟了不同的市场条件,并分析了由此产生的矿工行为。我们评估了一个用户矿工的盈利能力,该矿工获得了 100 万美元的前期资金用于购买矿机,但无法进一步扩大经营规模。模拟运行 100 天,取 25 次试验的平均结果。
用户的盈利能力是根据不同矿机类型和几种不同的电力成本来衡量的。亮点如下所示。
所使用的参数绝不是确定的,用户可以自由地用自己的假设重新运行分析。场景分析的代码可以在 main.py 中找到。
参考阅读:
https://github.com/khelmy/intelligent-bitcoin-miner/blob/main/main.py
牛市场景
我们的第一个测试是模拟了牛市的情景。考虑到撰写本文时正在进行的牛市,我们简单地将几何布朗运动模型与历史数据进行拟合。在这种条件下,价格逐渐上升到 10 万美元以上,沿途经历了几次修正。
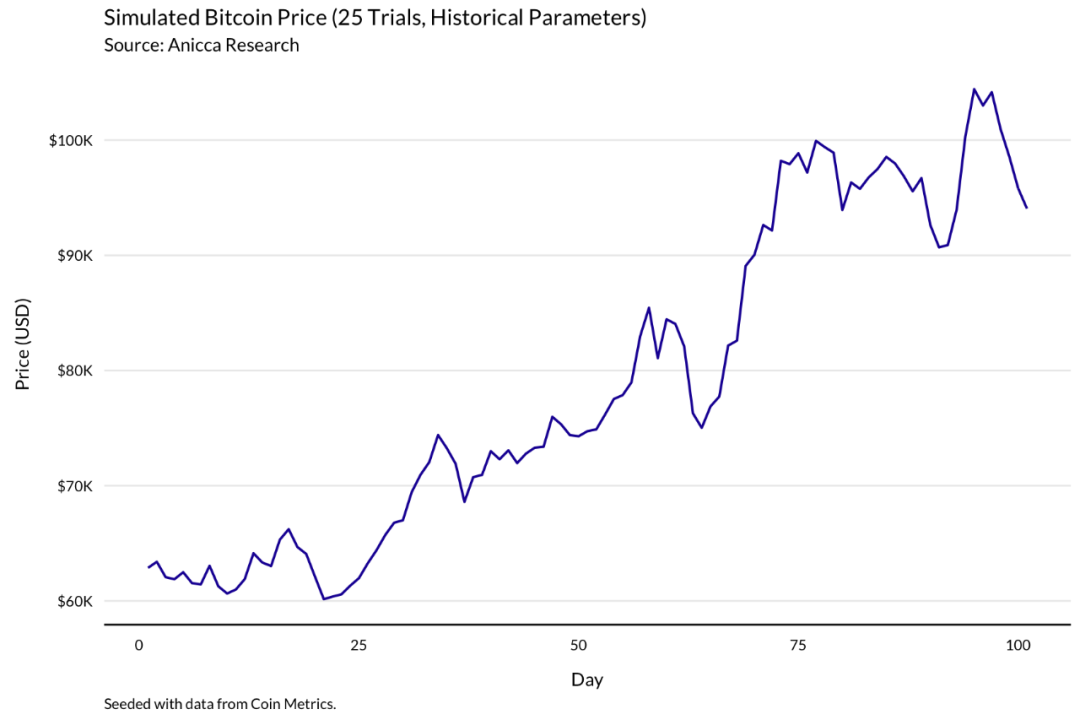
网络算力稳步上升,随着价格下调,经历了一些小型滞后修正。
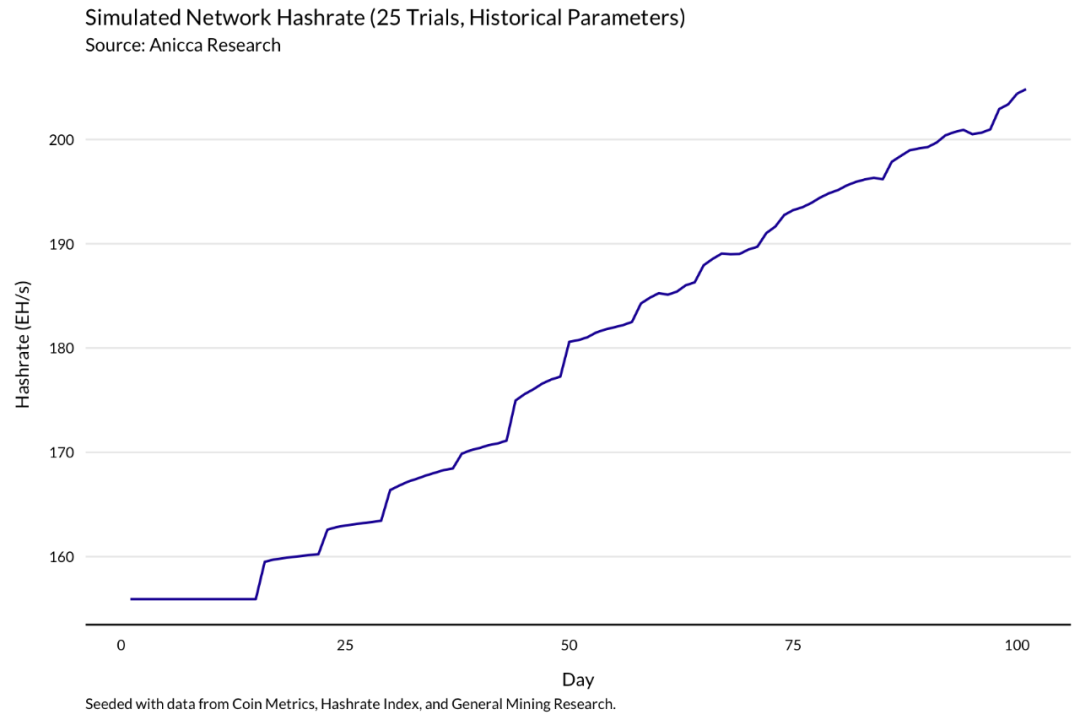
在这种情况下,相比每天卖出比特币,保留比特币仓位的利润要高得多即使电价很高也是如此。考虑到比特币价格的快速升值,这是有道理的。
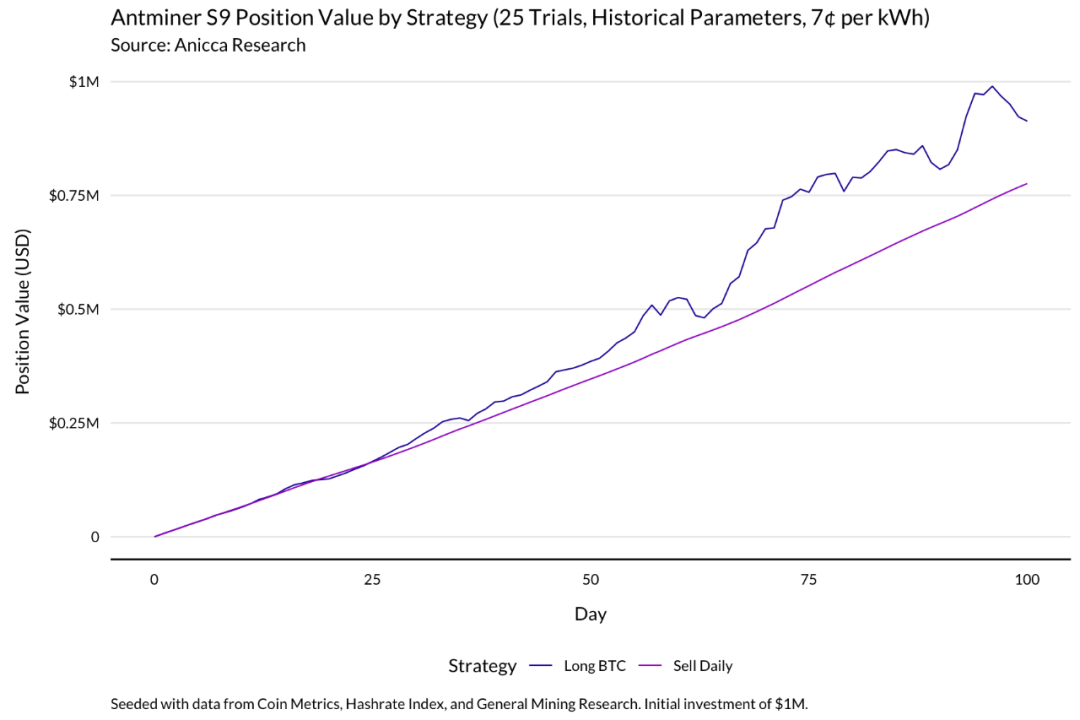
以一度电 4 美分的价格来算,只有使用 S9 矿机并在比特币中保持仓位的矿工才能在百日模拟期内实现盈亏平衡。
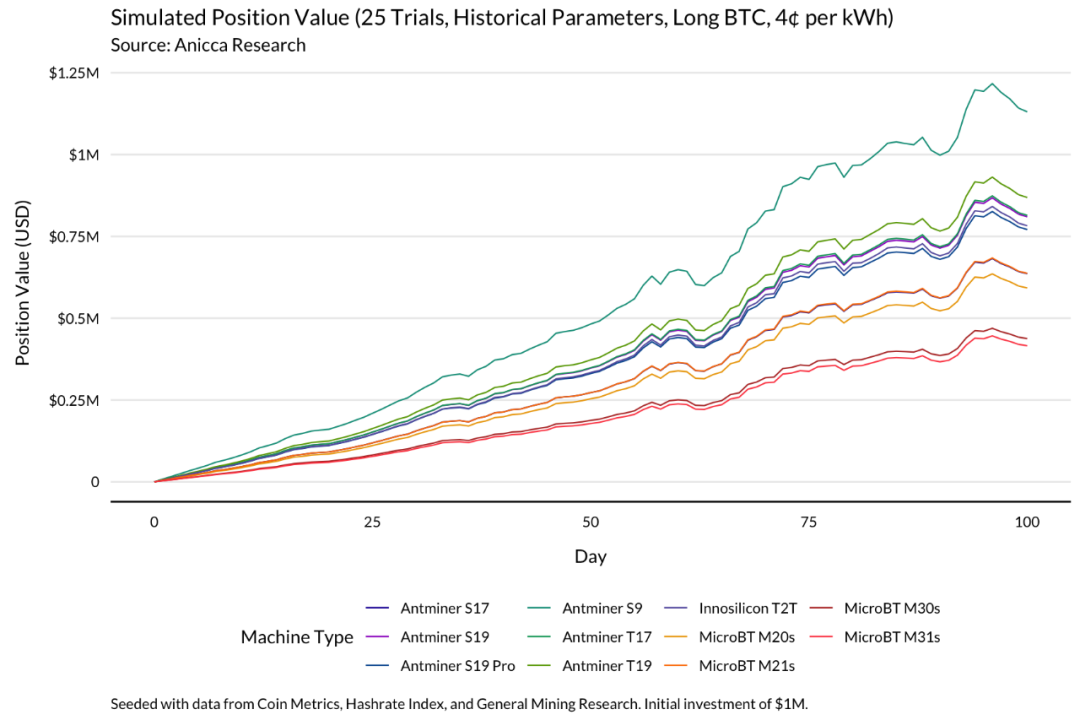
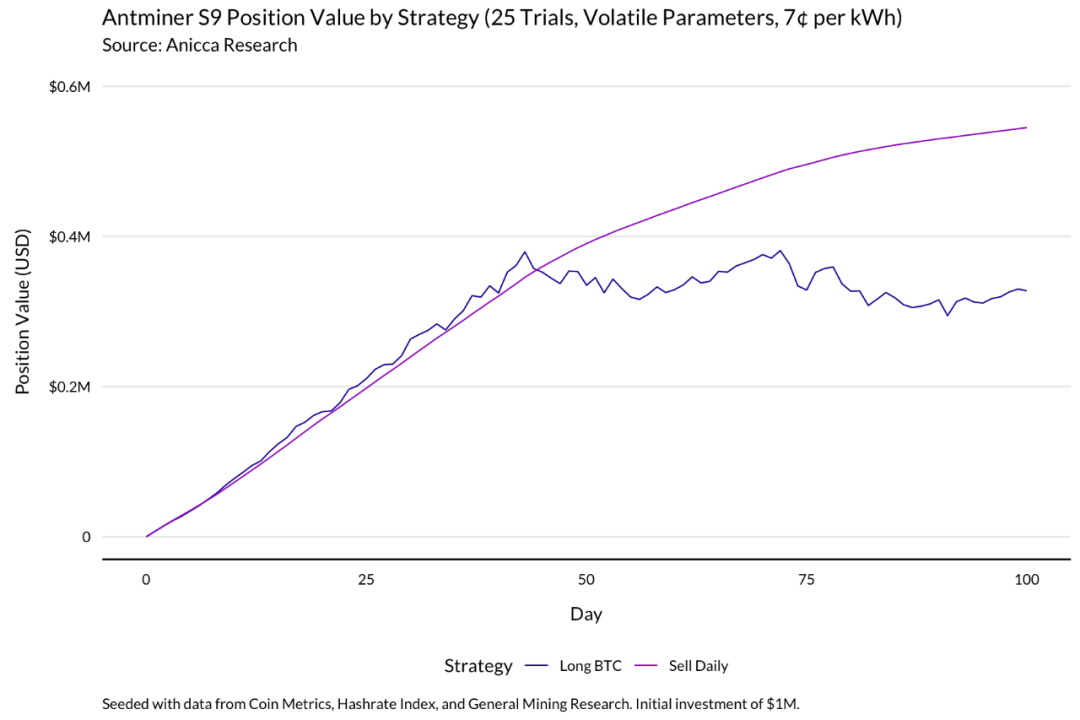
市场波动
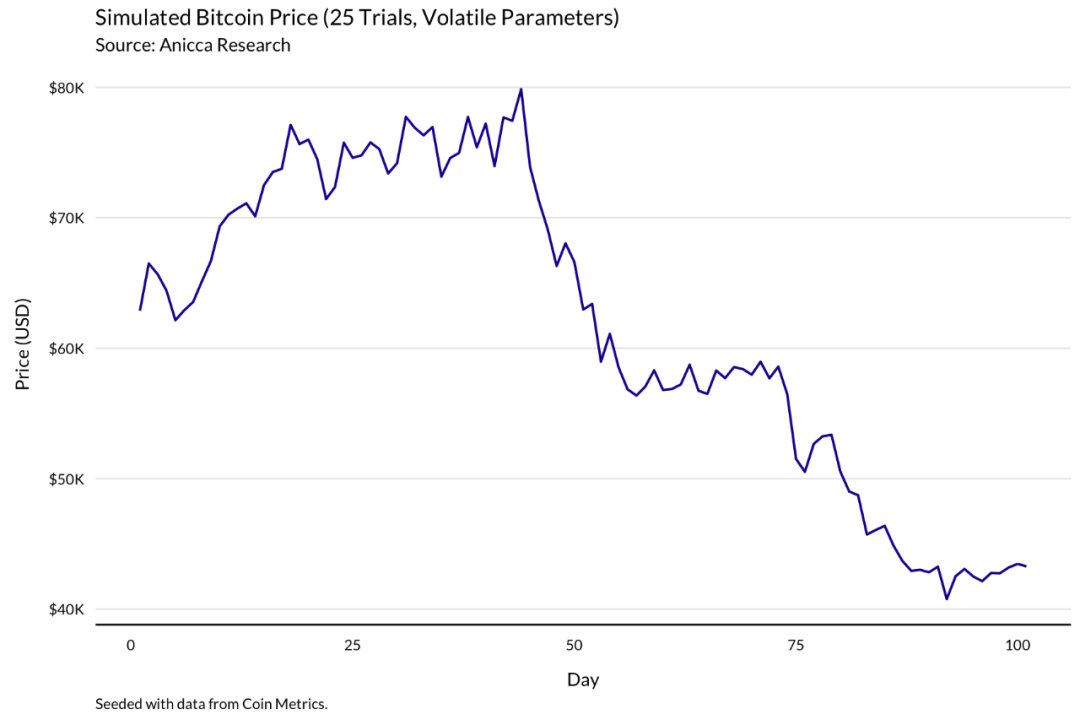
在第二种场景分析中,我们模拟了一个极为波动的市场,将历史拟合 GBM 模型中的波动项增加 25%,并将漂移设置为 0。价格最初上涨到近 8 万美元,然后暴跌到略高于 4 万美元。
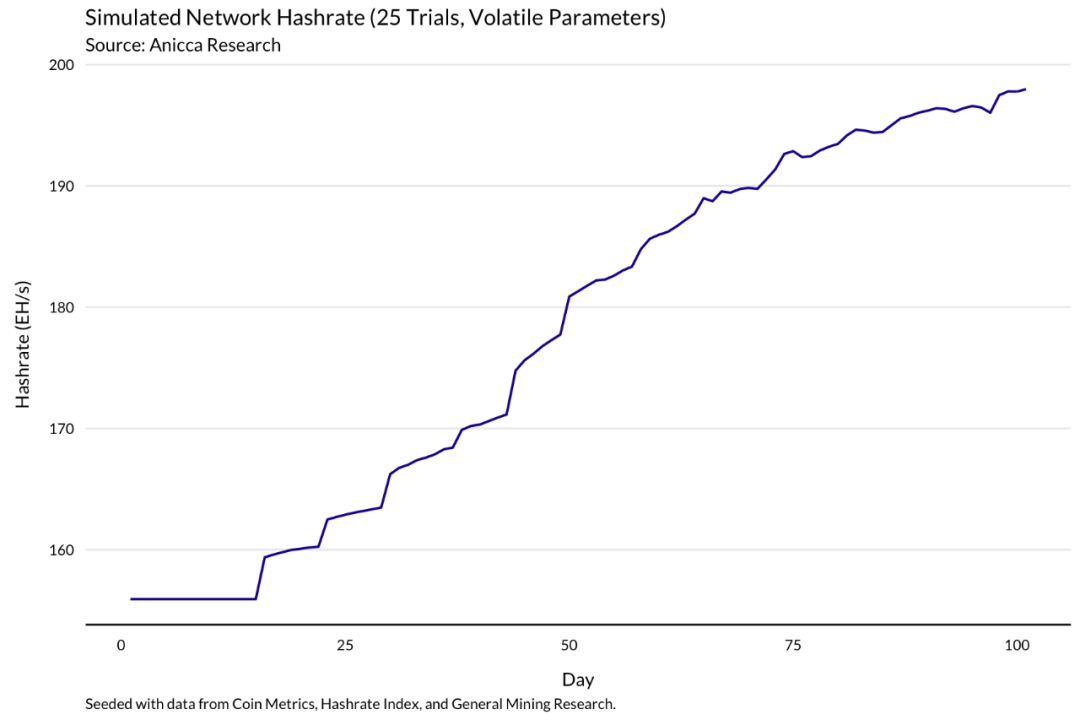
算力开始快速增长,但随着价格下降开始趋于稳定。由于响应延迟,算力会继续增加,但速度较慢。
最初,这两种策略的表现相当,比特币多头的表现略好于每天出清的卖家。随着价格下跌,有比特币风险敞口的矿工会因为承担了额外的风险而受到惩罚,持有的比特币市值下降。
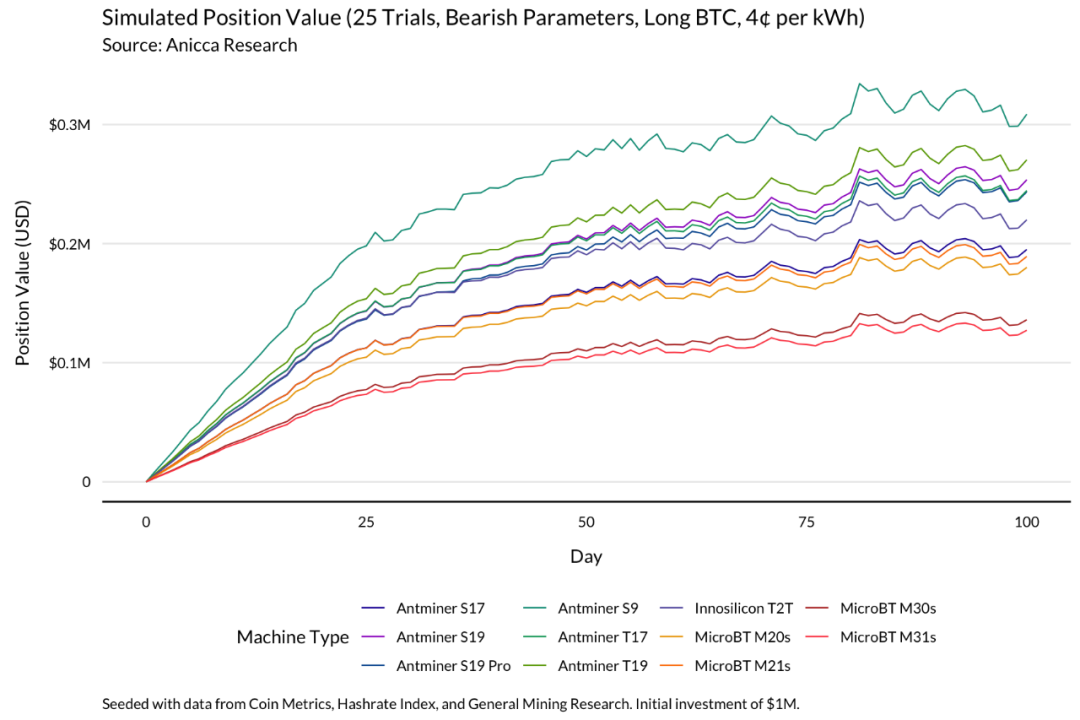
熊市
第三种模拟通过将 GBM 与历史数据拟合,并翻转漂移项的符号来模拟熊市。价格从目前的水平急剧下降,跌到近 3 万美元。

为了应对价格下跌,网络算力在最初的上升后进入修正。这就是《算力的炼金术》中介绍的从库存刷新到周期震荡阶段的过渡。

参考阅读:
《The Alchemy of Hashpower, Part II.》
https://www.aniccaresearch.tech/blog/the-alchemy-of-hashpower-part-ii
在熊市中,每个人都遭殃。比特币多头尤其如此:在每度电 4 美分的价格下,如果面临着比特币风险敞口,即使是最有效率的操作在模拟期内都无法收回一半的初始投资。
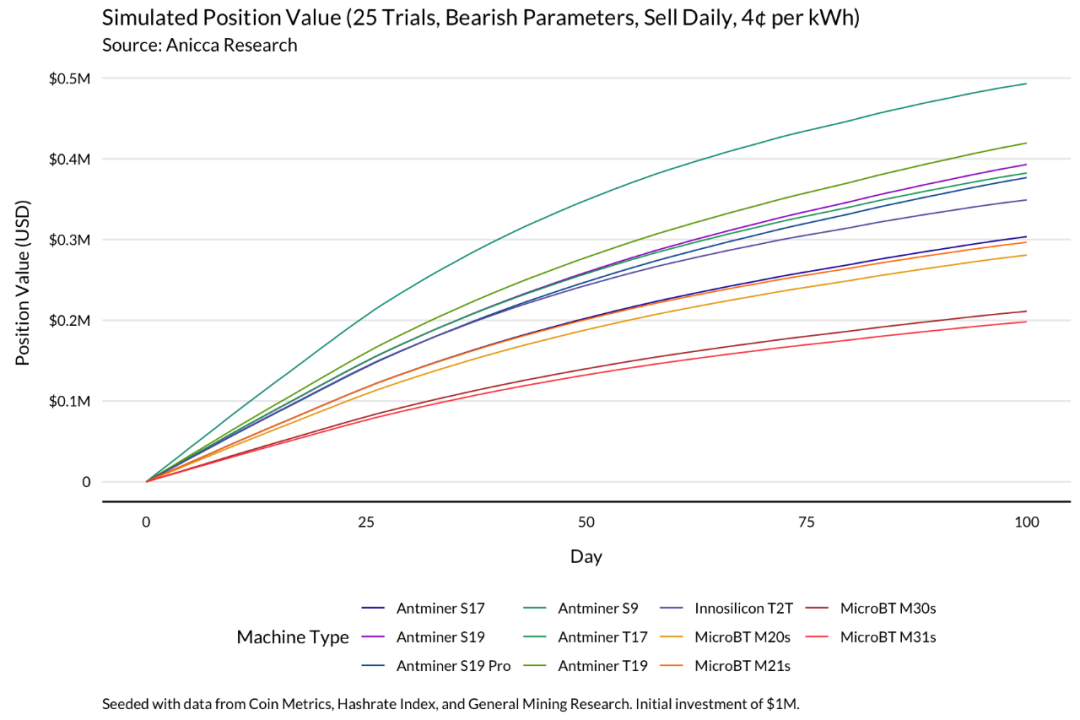
每日出清的卖家的表现明显要好一些,但由于他们的收益仍然取决于比特币的价格,因此表现仍然不如牛市时。
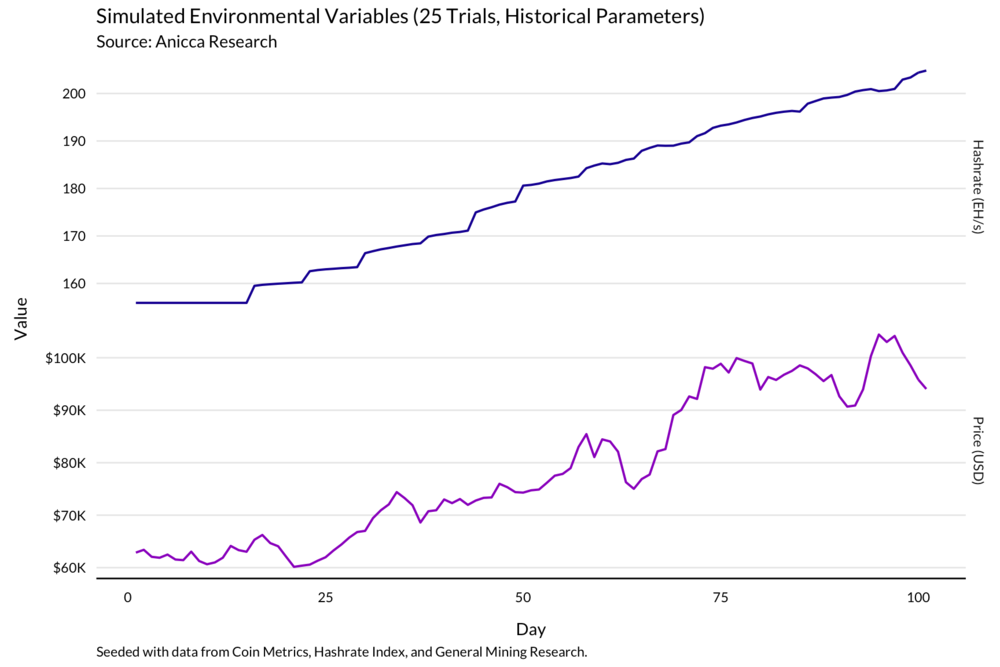
在牛市中,用旧矿机好还是新矿机更好?
场景 4 使用与场景 1 相同的历史参数,目的是比较在具有竞争性电价的情况下,运行新旧硬件的矿工的表现。
这一次,价格飙升到 14 万美元以上,一路加速。算力也迅速增加。
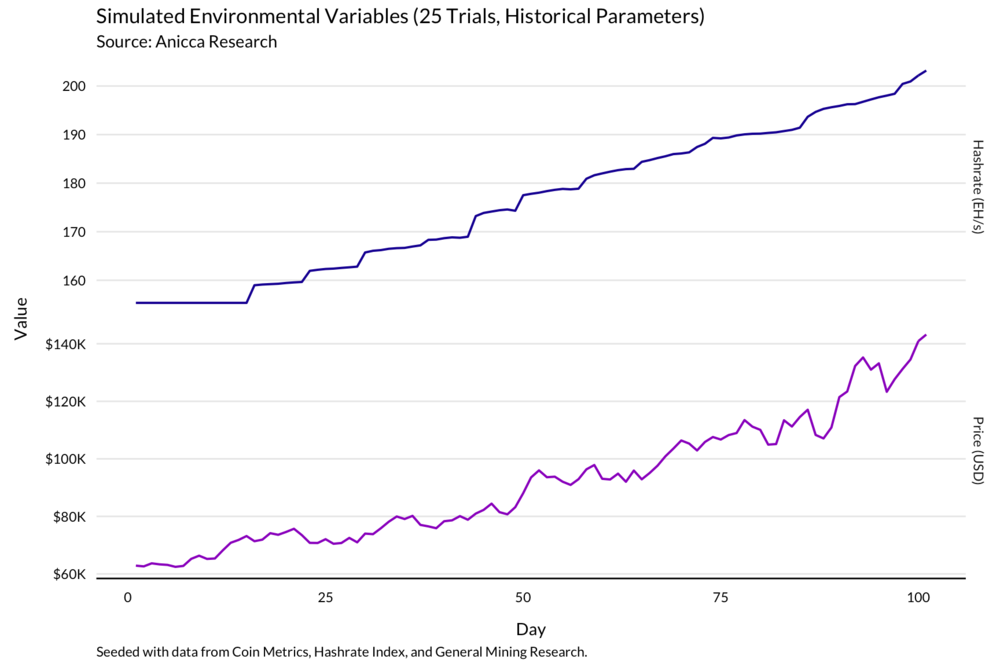
场景 1 vs. 场景 4
考虑到牛市的强度,即使是每天出清比利币的矿工,在运行 S9 矿机的情况下,也能在 100 天的模拟期内实现盈亏平衡。S19 矿机的利润要低得多,但仍能在每天出售的同时收回大部分初始投资。

在这种情况下,做多比特币的矿工盈利惊人。在模拟期间,运行 S9 的矿工投资基本上翻番,S19 矿工也能获得可观的利润。
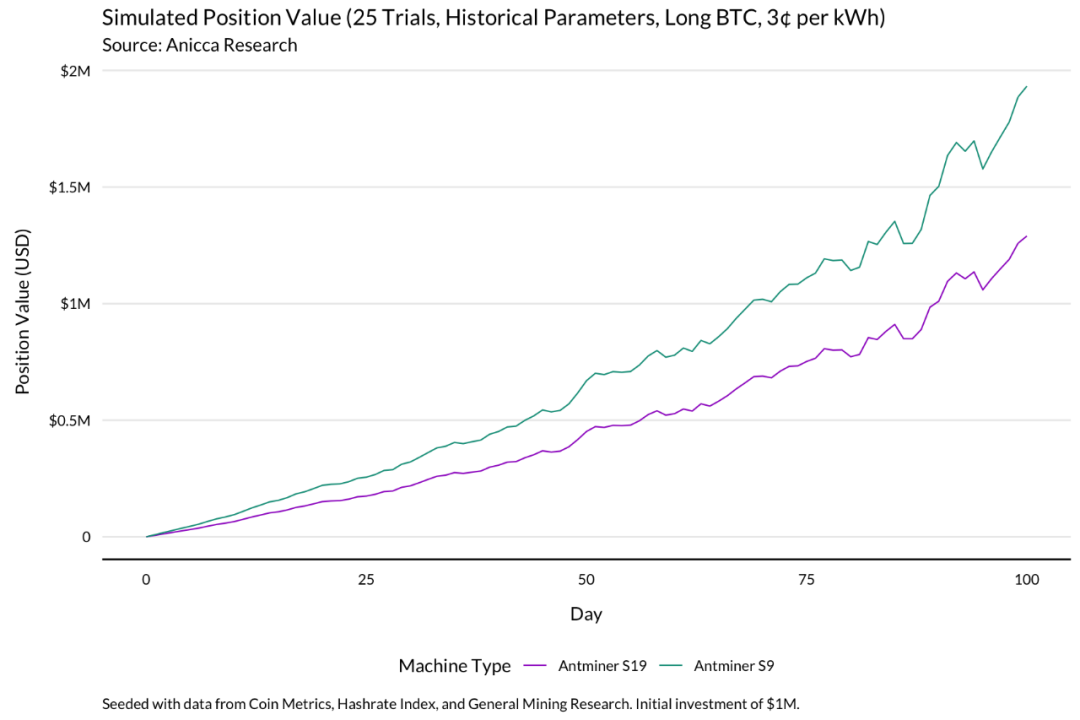
在熊市中,降低运营成本有多重要?
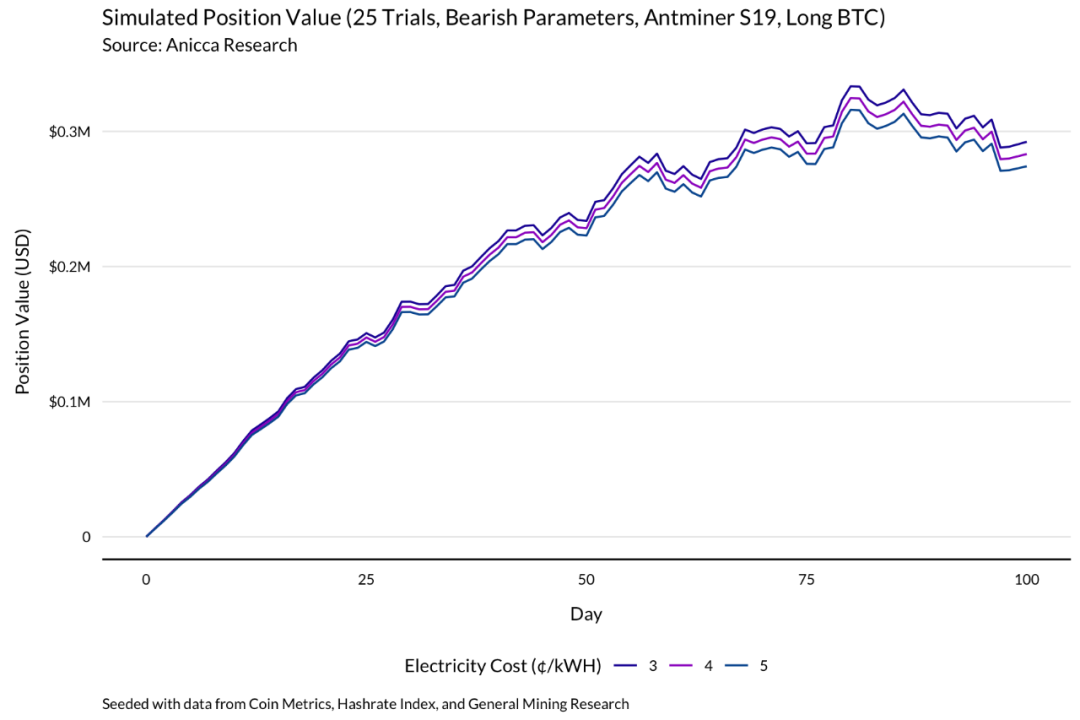
第五种也是最后一种模拟重新回到熊市中运行,这次的目标是分析电力成本对盈利能力的作用。为此,我们评估了 S9 和 S19 矿机在熊市条件下的表现,电费分别为每度 3、4 和 5 美分。
情形与场景 3 类似:价格暴跌,算力出现了一个较浅但长时间的修正。
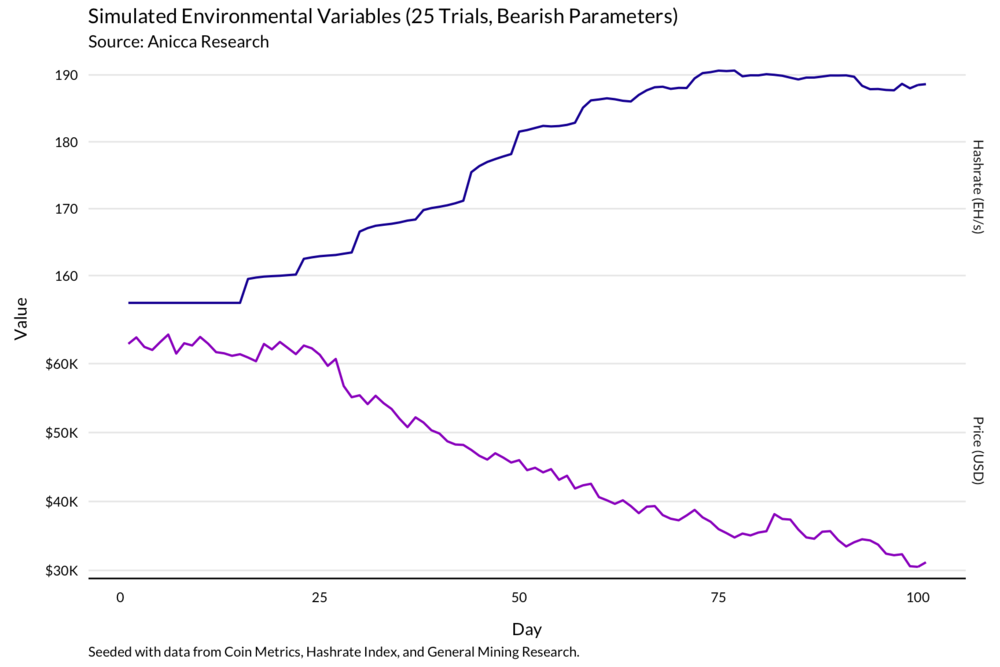
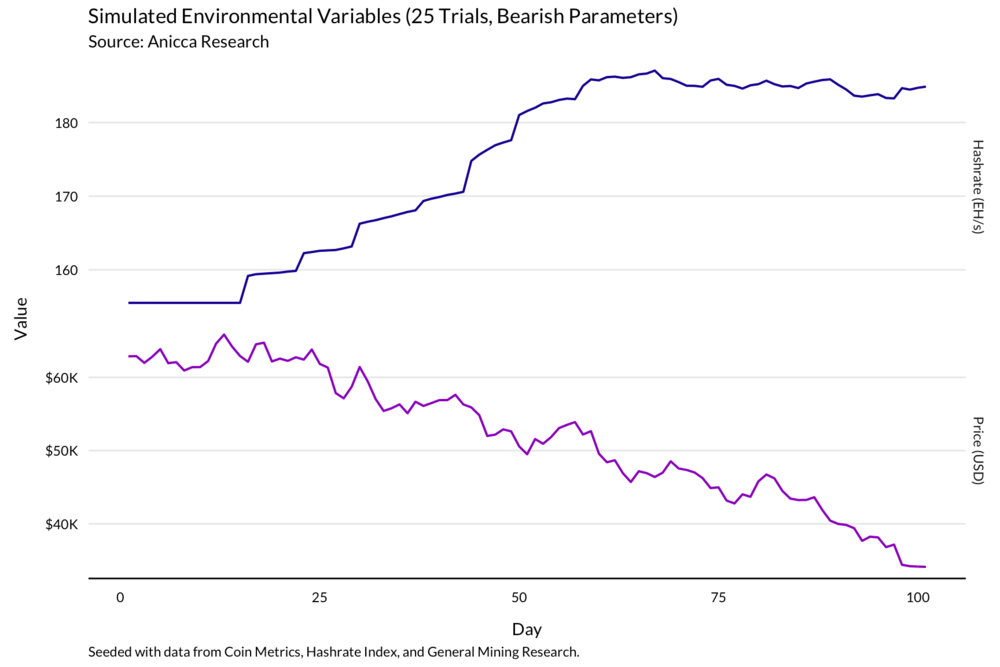
场景 3 vs. 场景 5
对于 S9 矿工来说,电力成本带来了实质性的差异。尽管在这些条件下,无论电力成本处在哪个水平,矿工的表现都不佳,但在电费为每度 3 美分的情况下,做多比特币的矿工的回报率接近其初始投资的 40%,如果电费换成是每度 5 美分,回报率则略低于 32%。

这种对电价的敏感性有助于解释为什么 S9 矿工往往会在电费更便宜的地区运营。
对于 S19 矿工来说,这种差异就不那么明显了。虽然电价较低的矿工仍然比电价较高的矿工赚得更多,但这一变量对盈利能力的影响要小得多。
结论
维度是统计学家的天敌,而比特币挖矿是一个很难建模的问题。即使是我们这种只做了几个简化假设的模型,也比我们最初设想的要复杂得多。像所有基于蒙特卡罗的工具一样,它的预测能力从根本上受到用户偏见的限制,这些偏见会从初始种子条件波及到一切结果。
参考阅读:
https://en.wikipedia.org/wiki/All_models_are_wrong
我们的模型明确假设价格和算力之间的关系是单向的,同时假定了可能相关的矿机模型和电力成本分布之间的独立性。所有的模型都是不全面的,但有些是有用的。
我们认为这个模型是有用的。在明智的比特币矿工的工具箱中,它应该能找到用武之地。













