正如标题所说，本文将不会介绍 Opyn 所提供的传统期权产品，而是重点解析由其开发的全新衍生品类别：Squeeth。该产品基于著名投资研究机构 Paradigm 于 21 年 8 月论文中提出的「乘方永续合约」概念进行构建。下文中，我们将使用尽量简明的语言和常见案例进行分析，所以没有金融基础的读者也不必劝退。

一提起衍生品，人们往往会联想到投机者用来赌涨跌的高杠杆投机工具。但实际上，衍生品原本是为了帮助用户更高效地转移风险（类似于买保险）。因此，本文中我们不会简单的将 Squeeth 视为一个新出现的高杠杆投机手段，而是回归其本质属性，看看当用户在面对自己不想承担的风险时，Squeeth 可以发挥哪些作用。

Crypto 用户最常见的应用场景恐怕便是流动性挖矿了。蓬勃发展的加密世界为用户提供了远超传统行业的收益率。然而当用户参与挖矿活动时，往往会被迫持有一些自己完全不了解也不想持有的 Token。在下文的两个案例中，我们将直观地解释 Squeeth 是如何帮助投资者转移双币矿池的「无常损失」风险的。

不过由于双币池的模型更为复杂，因此让我们先从一个更加简单的单币池案例入手。

如何无风险白嫖单币神矿的收益？

你突然发现了一个名叫 JQK 的项目正在举办单币质押返利活动，年化收益率高达 500%。你不知道也完全不想知道这个名叫 JQK 的项目到底在做什么，你只想白嫖他 500% 的收益，这时你应该怎么做？（在理想环境下，不考虑合约漏洞、衍生品价格脱钩等其他风险）

你拿出 1000 美元作为本金参与这项投资。依据活动要求，首先你需要将这 1000 美元兑换为 JQK 质押进项目合约。而一旦你将 1000 美元兑换为你完全不了解的 JQK，那么这 1000 美元资产后续的市值，将直接受到 JQK 价格波动的影响。

如果把你这时持仓的全部资产的市值作为纵轴，JQK 的价格作为横轴，我们将得到你投资组合的市值曲线。

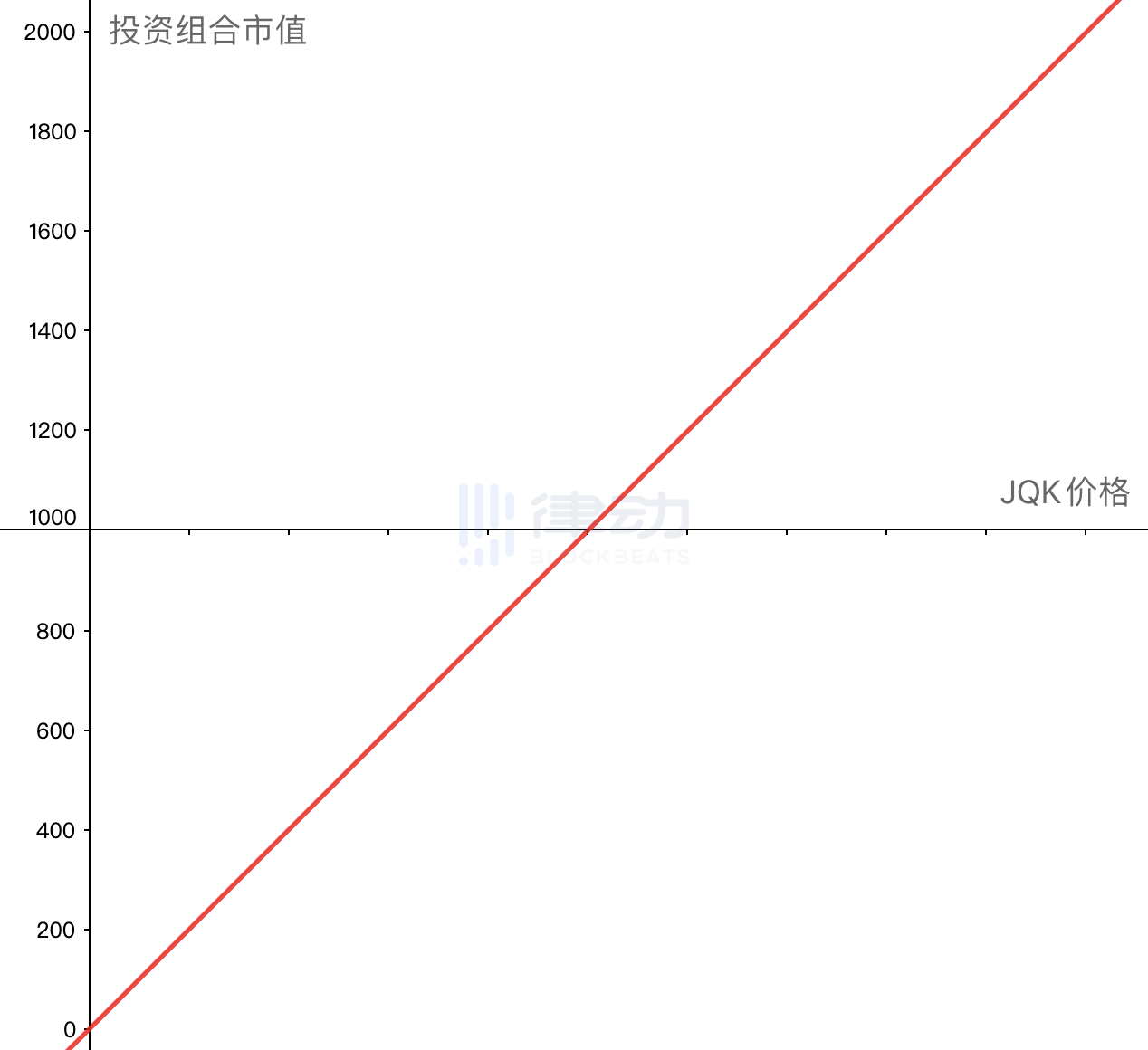由于你只是想享受高达 500% 的挖矿收益，既不了解也不想承担持有 JQK 的风险，因此你希望能够将这部分风险转移，使得 JQK 的涨跌与你不再相关。也就是说，你希望你的投资组合市值曲线变为一条水平直线。

这时，你可以使用 JQK 的期货或永续合约做空同等数量的 JQK。购买 JQK 空头头寸的市值曲线如下：

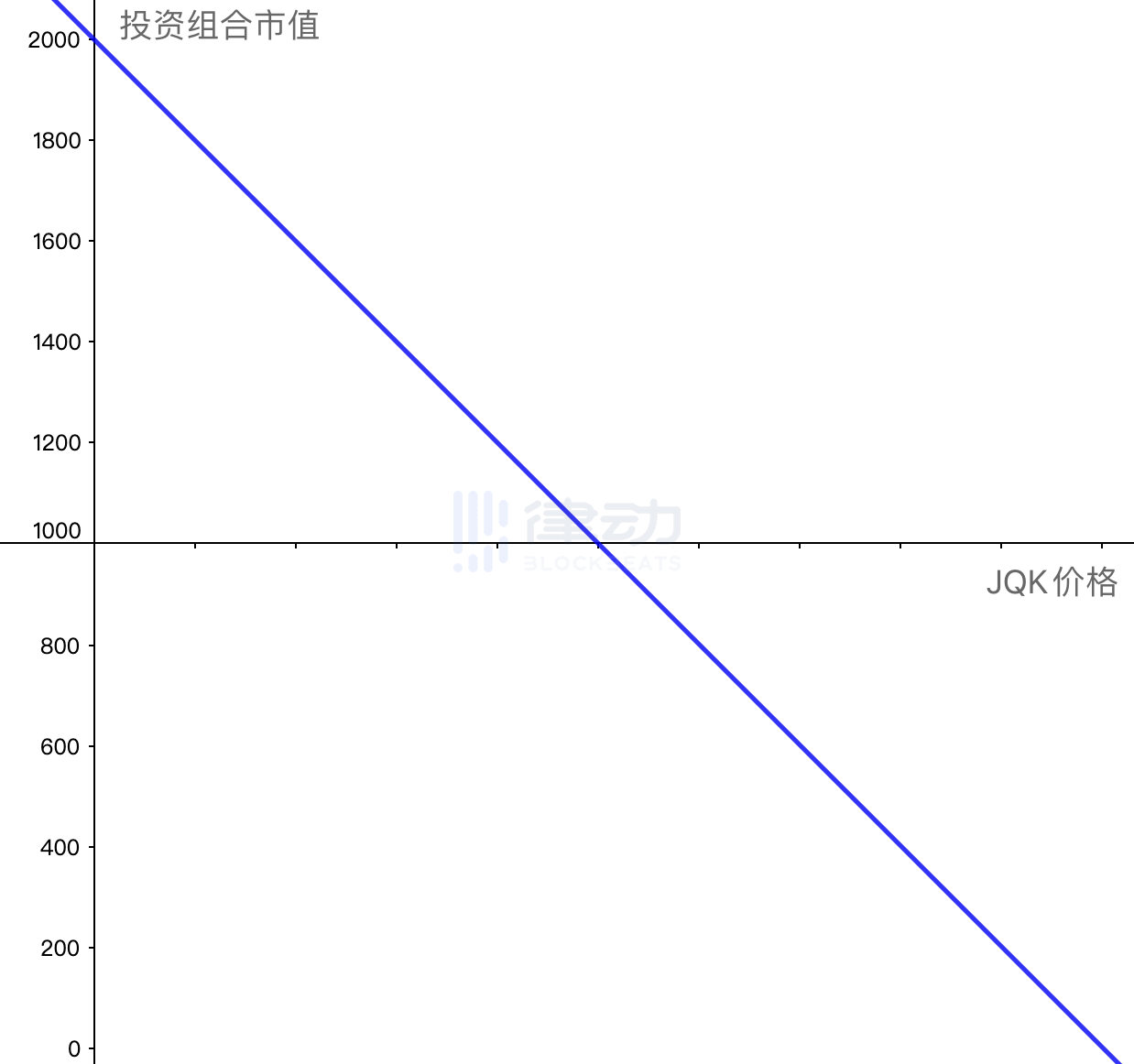可以看出，图 2 的斜线正好是刚才图 1 的倒影。因此如果将两者同时加入你的投资组合，那么两者结合的最终结果，便是在每一个点将两者的损益相加。

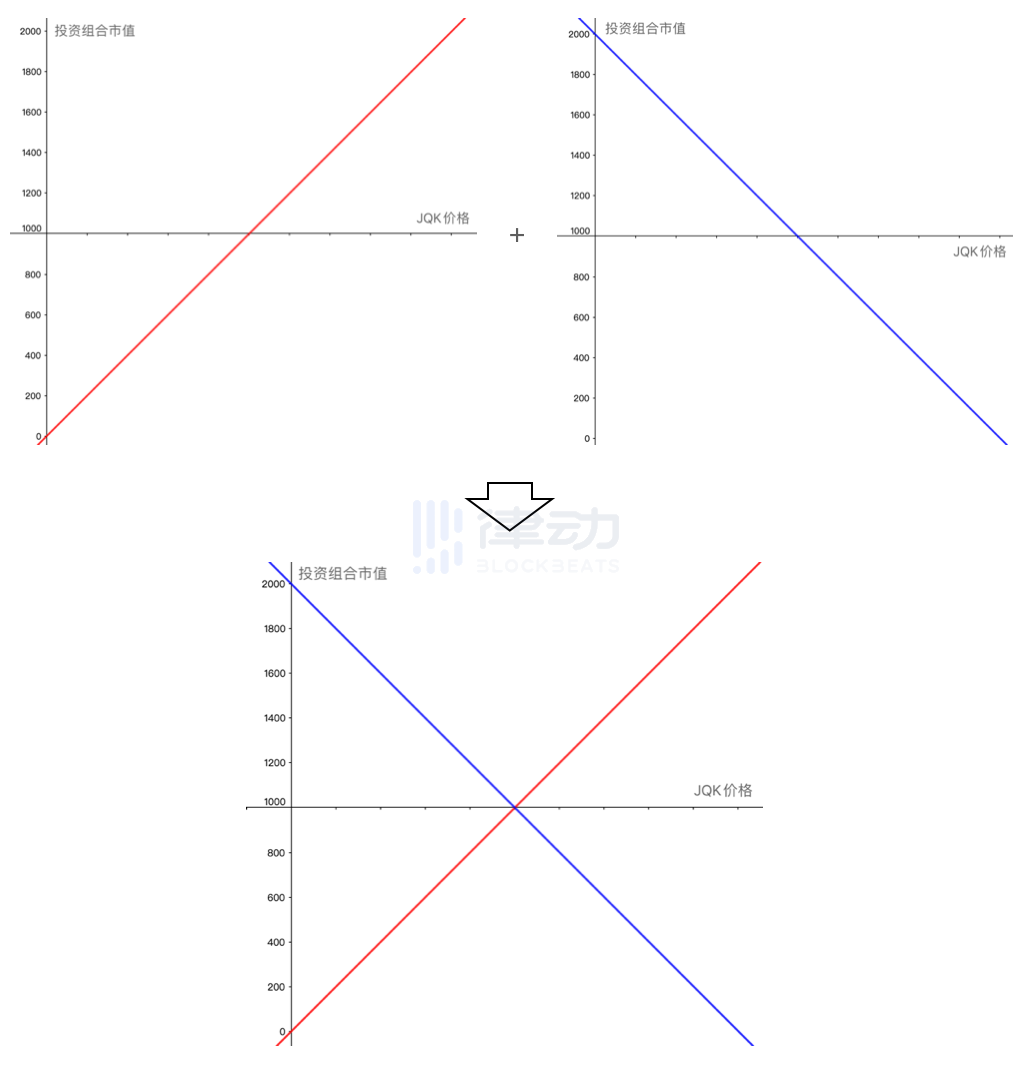由于两者在每个点的损益大小相等但方向正好相反，因此相加的结果，便是一条水平的直线。这时，你便可以无风险的享受 500% 的稳定收益，而不再需要担心 JQK 的价格波动风险了。

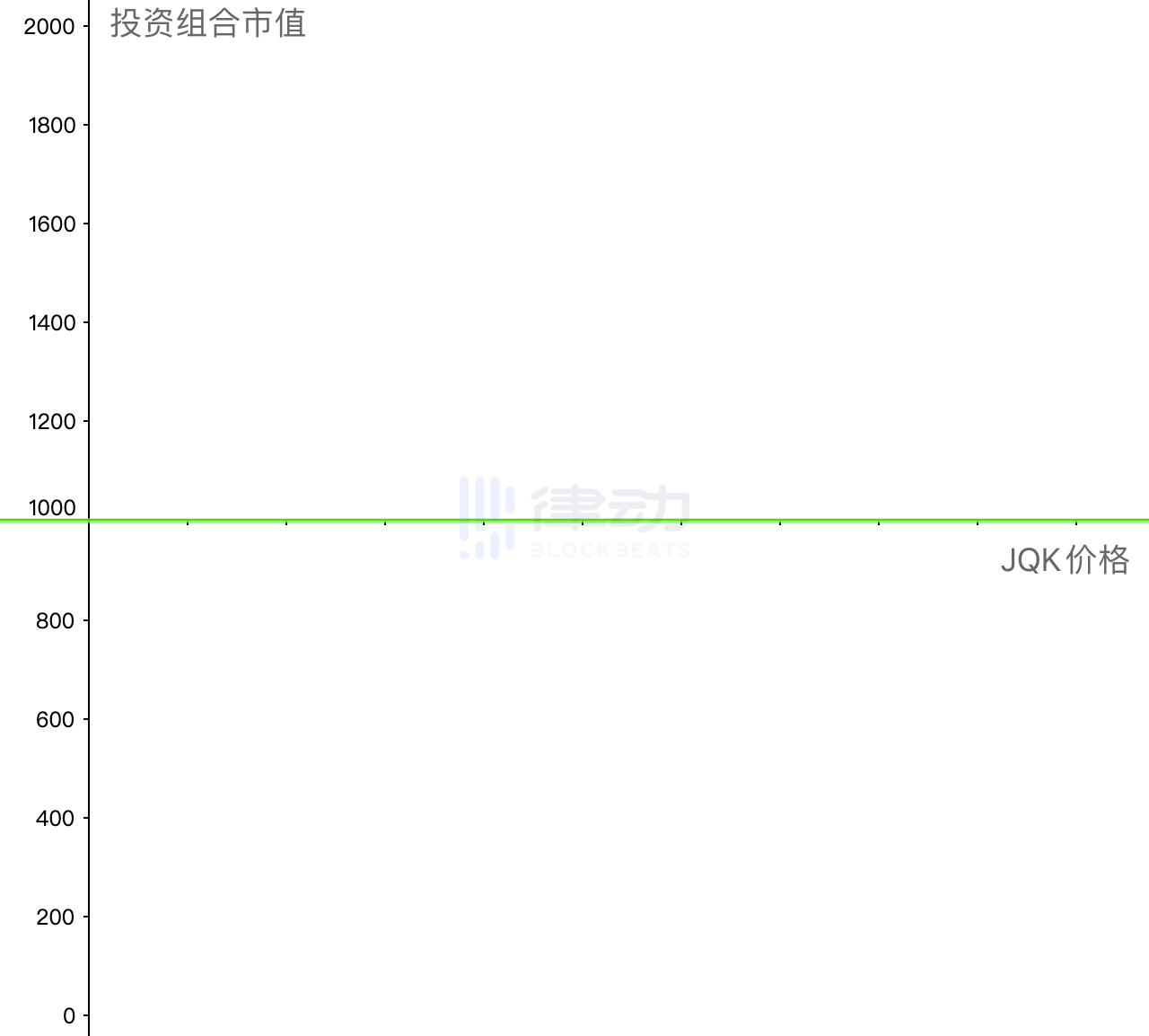
刚才这种操作专业的叫法便是套期保值，有时也被称为对冲，主要用于帮助投资者转移其不想承担的风险。在了解了简单的单币池风险转移方式后，我们再来看一下更加复杂的双币池。

如何无风险白嫖双币矿池的收益？

假设你又发现了一个名叫 QKA 的项目，正在某个 AMM 交易平台中举办双币流动性挖矿活动，年化收益率高达 500%。你不知道也完全不想知道这个名叫 QKA 的项目到底在做什么，你只想白嫖他 500% 的收益，这时你应该怎么做？（在理想环境下，不考虑合约漏洞、衍生品价格脱钩等其他风险）

从之前的案例中我们已经学到，想要无风险挖矿，就需要将投资组合的市值曲线调整为水平直线。因此，首先我们需要知道双币的 LP 头寸的市值曲线本来是什么样子的。

相比较单币池的图像，双币池的图像显然复杂了许多。首先，双币池的图像从直线变为了曲线。因此首先我们要解决的问题，便是将这条变弯的曲线掰直。

这时，我们就需要找到一个新的衍生品帮我们完成目标了。对于这个新的衍生品，首先他本身的市值曲线必须也是弯曲的，因为只有这样才能被用来反向对冲。其次，这条曲线弯曲的方向，必须和双币池的弯曲方向相反。

这时，本篇文章的主角 Squeeth 终于可以出场了。我们先不解释 Squeeth 到底是什么，先来看看他的市值曲线。

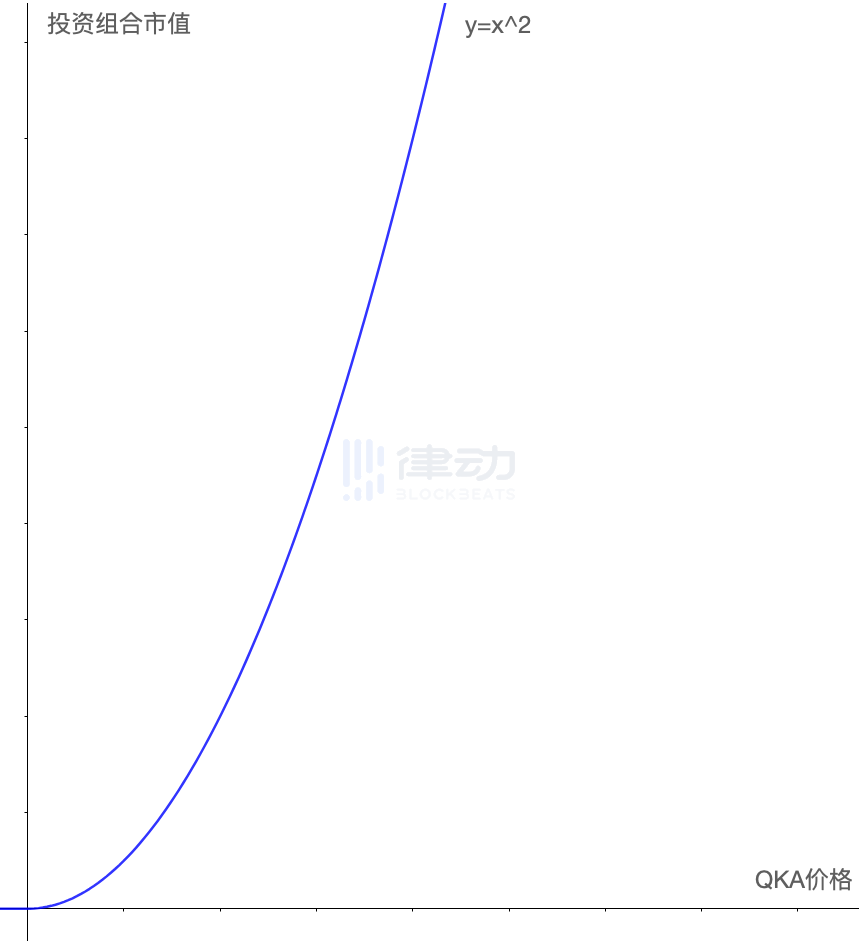可以看出，Squeeth 的曲线形状完美的满足了我们最开始提出的条件。不但本身也是弯曲的曲线，而且和需要对冲的曲线弯曲方向相反。因此，只要我们调整好两者混合的比例，那么就有希望将两者拟合为一条直线。

经过尝试，我们将两条曲线按照 1:100 的比例混合，最终拟合的结果便是下图中绿色的曲线。可以看出，除了在极端值（QKA 价格极小或极大）以外，绿色曲线已经很接近一条直线了。

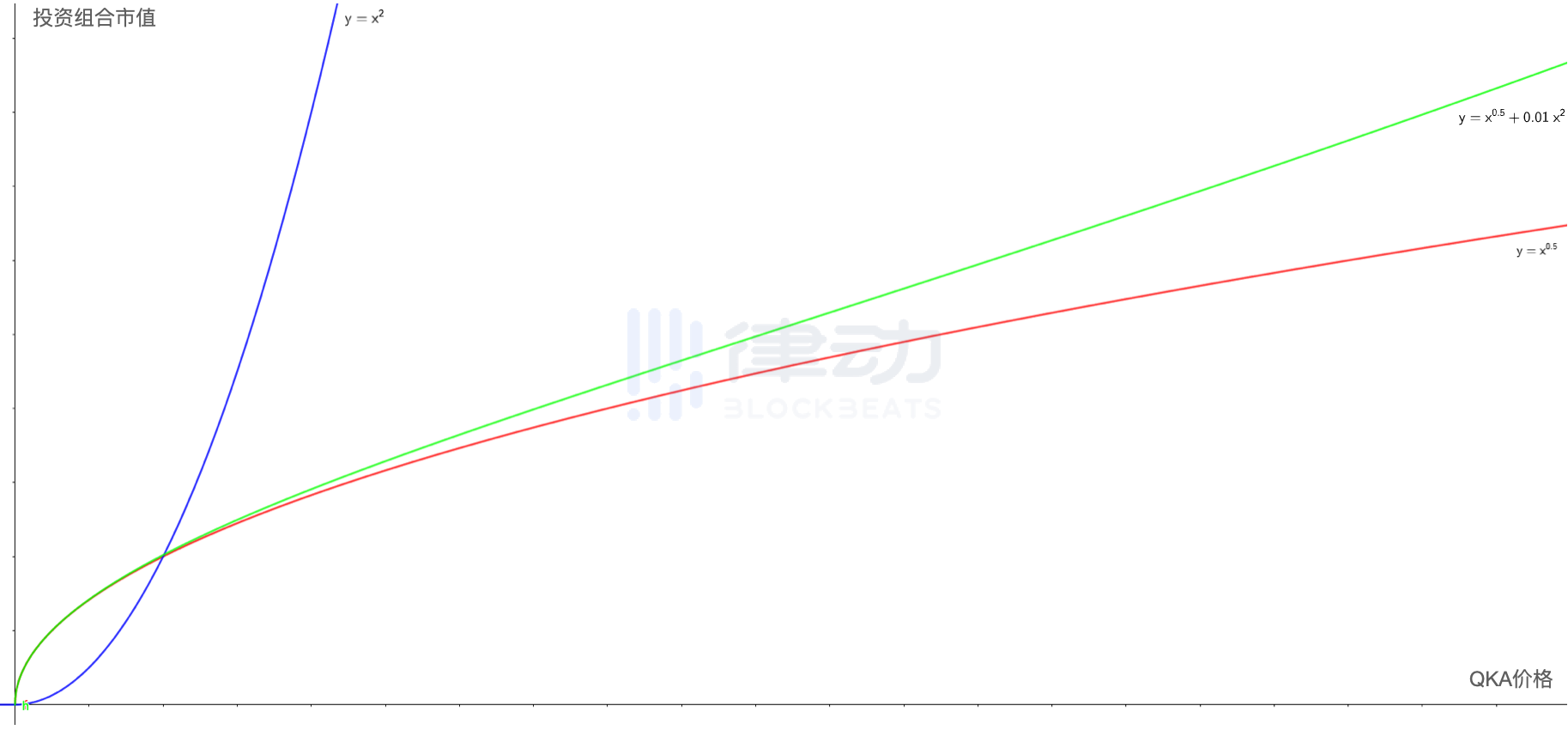后续的工作便很简单了，对于这条还有一定倾斜角度的绿线，只要再按照案例一中的方式，使用永续合约或期货对其斜率进行微调，那么便可以达到我们最初的目标。这里以大概 3:1 的比例对两个函数进行混合，我们便能得到图中黄线表示的新的函数图像，能够看出已经非常接近于一条水平直线了。

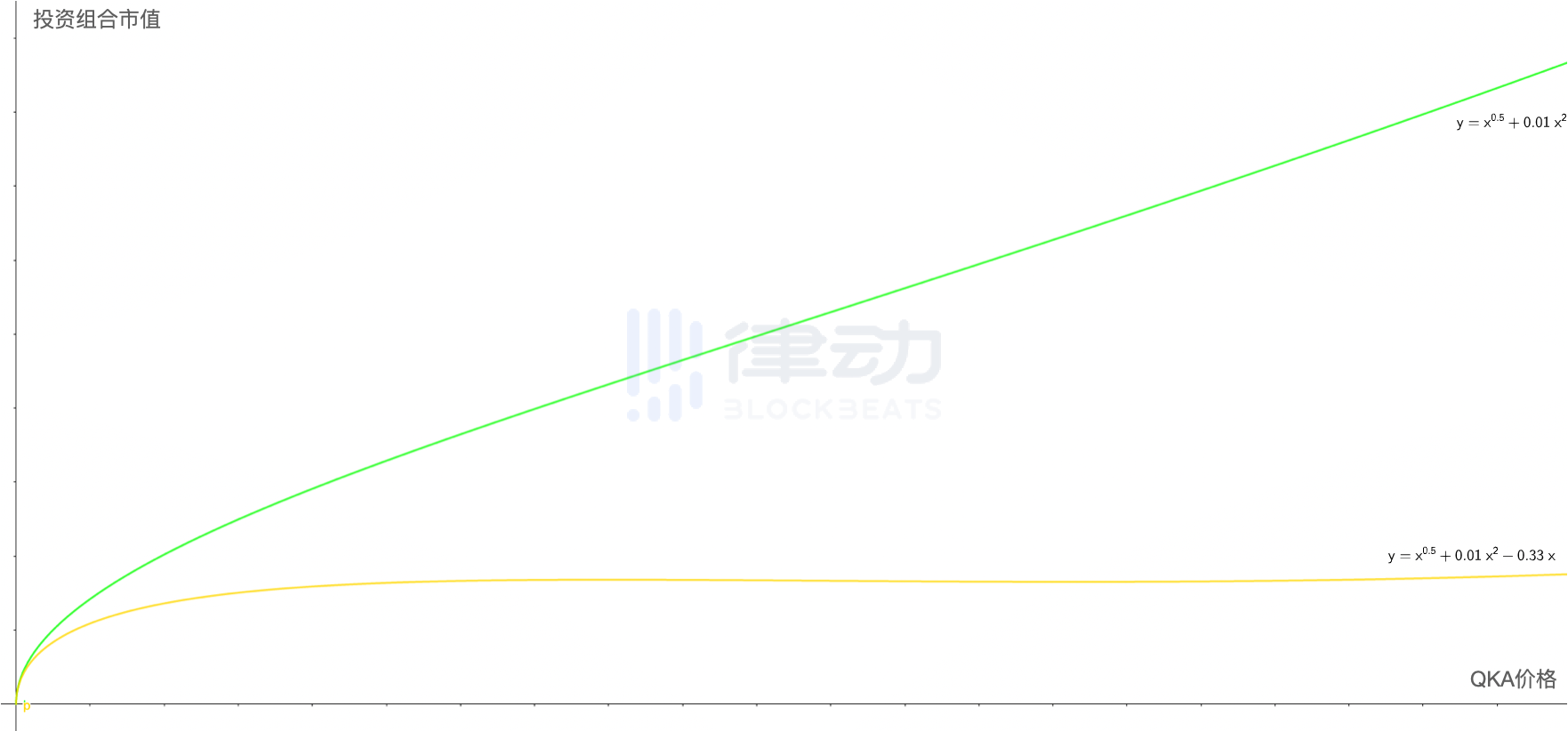这时，只要 QKA 的价格不归零，你便又可以开开心心地白嫖这个双币池 500% 的无风险收益了。（注：以上所有案例都不是严谨的数学证明，只为直观地展现整个过程背后的主要逻辑）

刚才提到的第二个案例，便是 Squeeth 未来最可能的应用场景。这里我们不再详细分析 Squeeth 背后乘方永续合约的基本原理，只在这里对其特点进行简要的概括，想要详细了解的读者可以回顾我们早期的一篇解析文章：《如何理解 Paradigm 的乘方永续合约》。

1. 乘方永续合约本质上不是期权，其基本产品逻辑更像永续合约；

2. 乘方永续合约与永续合约最主要的区别，便是其目标函数由 y=x 变为了 y=x^n；

3.Squeeth 是乘方永续合约在 n=2 时的特殊形式；

4. 由于乘方永续合约在函数图像上与期权同样表现为曲线，因此具有与期权而不是期货更相似的使用场景，故而也被称为类期权产品（像期权但又不是期权）；

不过自论文发布后，乘方永续合约一直只是个停留在学术论文阶段的新颖概念，想要把他变为真正实际可用的产品，依然需要大量复杂的设计开发工作。

乘方永续合约的产品化：Squeeth

自论文发布后至今的近半年时间里，Opyn 团队一直在对其具体的产品方案进行更加详尽的工程设计，过程中自然也面临了许多棘手的问题。

相比传统的永续合约产品，Squeeth 的目标函数 y=x^2 的价格波动幅度更大，传统永续合约的保证金交易模式很难直接套用到 Squeeth 上。但如果不采用保证金交易，维持永续合约价格锚定的资金费又失去了支付的手段。

以上这些问题如果不能得到有效解决，Squeeth 的产品设想恐怕只能停留在理论阶段。因此，Opyn 团队对其交易模式进行了大胆的创新。

1. 改进保证金交易机制

传统的永续合约交易平台基本都依赖保证金交易制度，这个机制在给投资者带来杠杆交易功能的同时，也使得投资者的交易头寸无法脱离保证金平台而独立存在。也就是说，投资者在平台中持有的头寸很难被通证化。这使得这些头寸只能被限制在一个封闭的空间内，难以享受到加密世界的超额流动性支持。

为了使得 Squeeth 的持有者免除缴纳保证金，Opyn 直接将产品的多头持有者的杠杆倍数锁定到一倍。由于免除了清算风险，因此得以直接将 Squeeth 产品的多头头寸通证化。Squeeth 被通证化后的名称为 oSQTH，这个通证完全可以脱离 Opyn 平台自由交易。需要使用 Squeeth 对冲风险的用户可以直接通过 Uniswap 购买。

但同时，由于 Squeeth 空头头寸持有者的亏损幅度无下限，因此并不能像多方那样免除保证金。在铸造 oSQTH 之前，空方需要先向平台质押一定数量的 ETH，以保证在极端情况下可以进行清算。

读到这里你可能已经发现，Squeeth 产品已经从最初的保证金交易的永续合约类产品，演化为资产铸造与发行平台了。

2. 变革资金费支付方式

我们知道维持永续合约类产品与目标函数价格锚定的基础是资金费制度，然而变更为资产铸造与发行平台后，这个最基本的基础也不存在了。为了解决这个问题，Opyn 发明了新的锚定机制。这种机制，被称为实物支付方式（in-kind funding）。

实物支付的思路也很简单，既然没钱，那干脆就用持有的 oSQTH 通证代为支付吧。在这种设想下，oSQTH 的持有者在向空方支付后持有的 oSQTH 资产变少，同时空方收到 oSQTH 后，其赎回 ETH 需要归还给系统的负债也同时减少。

不过既然多空双方的资产与负债同时同比例减少，能不能索性也不要频繁支付 oSQTH 了，直接调整 oSQTH 对 ETH 的相对赎回价格？

我们举一个实际的例子。空方最初质押了一个 ETH 用于发行 100 单位 oSQTH。一个月后，按照市场成交价格计算出的资金费率应为 10%，这时系统不再从多方的账户内扣除 oSQTH，而是直接将空方赎回 1ETH 需要归还系统的 oSQTH 数量从 100 调整为 90 单位 oSQTH。

这样，空方的负债直接减少了 10%，等同于赚取了 10% 的利润。这个调整空方负债归还比例的参数，便被称为 normalization factor。

这种模式很像 Compound 的计息方式，存款人持有的 cToken 数量并没有随利息的增加而增加。但是系统会不断调整 cToken 与存入资产的兑换比例。当你取回资产时，同样数量的 cToken 可以赎回比存入时更多的原始资产，超额部分便是存款人的利息。

这样设计最大的好处，是使得资金费的支付不再需要进行频繁的链上交易。但由于所有资金费带来的影响都直接体现到了 oSQTH 通证的价格中，因此长期来看 oSQTH 的价格相对于其所跟踪的 ETH^2 也必将出现偏离。

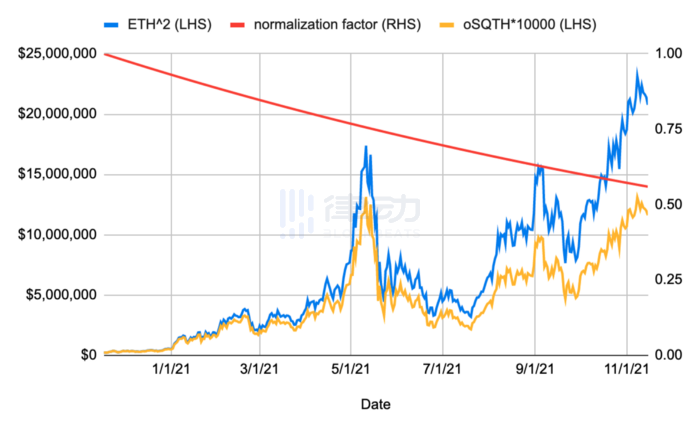正如上图所显示的，黄色 oSQTH 的价格将逐渐低于 ETH^2 的目标价格，这部分差异便是多方累计支付的资金成本。其偏离程度随着红线所代表的 normalization factor 参数的价格降低而逐渐拉大。

Squeeth 的意义与不足

1. 主要意义

Uniswap 与 Curve 是目前以太坊生态中两个最为重要的 DEX 项目，其中全功能的 Uniswap 相比主要针对稳定币的 Curve 有着更加丰富的应用场景。但我们从两者的资金锁仓量上，却看到了完全相反的现象。很长一段时间内，Curve 的锁仓资金总量都远远大于 Uniswap。

这其中一个不可忽视的因素是，Curve 的资金池不论稳定币还是非稳定币，其内部都自带无常损失管理机制，这使得 Curve 的 LP 们完全可以将其当作被动管理基金购买，并不需要随时关注无常损失问题。

而反观 Uniswap 的 LP 们，无论是在 V2 还是 V3 版本中做市，无常损失都是一个无法被忽视的问题。如果 LP 们放任不管，其存入的资金往往在一段时间后反而不如之前。

虽然目前有不少减少 Uniswap LP 无常损失的解决方案，但这些项目往往基于主动调仓的机制。直到 Squeeth 的出现，被动管理 Uniswap LP 无常损失才有了新的方案。未来，或许可以由项目方，基于 Squeeth 与常规永续合约等衍生品，构建无风险的 Uniswap 资金池。使得 Uniswap 的 LP 们也可以像在 Curve 一样，获得被动且无风险的做市手续费收益。

此外，Squeeth 产品还通过底层创新解决了传统期权类产品最严重的缺陷，那就是由于行权价与到期日带来的流动性割裂问题。如果事实证明 Squeeth 真的能够在多数应用场景下替代掉传统期权，那么其对于金融行业发展的意义必将是无可估量的。当然，这个结论依然需要经过真实市场的检验。

2. 缺点与不足

严格来说，Squeeth 并不能完全对冲所有形状的曲线。即便是上文中所举的双币池案例，Squeeth 也无法做到完美对冲，只能做到大致将曲线拉直。理论上，想要完美对冲 AMM 资金池的双币头寸风险，需要开发 n=0.5 的乘方永续合约产品，不过这个需求恐怕要等 Opyn 的下一阶段产品开发计划了。

此外对于普通用户来说，Squeeth 的使用方式依然显得过于复杂。因此，希望 Opyn 未来不要仅仅推出一个名为 oSQTH 的通证，而是能够针对特定场景，设计一些简单可用的综合性解决方案，让用户在不需要了解衍生品基本逻辑的情况下，也可以一键转移风险。或许这样的服务，才是衍生品领域真正能够破局的杀手级应用。

最后，Opyn 的 Squeeth 产品预计将于 1 月 10 日上线以太坊主网，并于 1 季度末登陆以太坊 Layer2 平台，届时用户可以前去体验。

文末加餐——期权希腊值

正文中为了更直观地解释套期保值的基本原理，我们在案例中使用了过多如倾斜、弯曲等描述性词汇。但是在实际操作中，我们依然需要定量的参考指标，以便我们计算为了转移风险而需要购买的衍生品数量。这种定量的参考指标被习惯性的用希腊字母来表示，以下我们便用白话介绍其中最常见的三个希腊值。（当然以下表述也并不严谨，只为让初学者有个直观的感受）

1.Delta（倾斜程度）

Delta 用于描述投资组合价格曲线的倾斜程度。倾斜的越严重 Delta 值就越大，向上倾斜为正，向下为负。因此如果你知道你的投资组合的 Delta 值是 1，那么你需要用于对冲的衍生品的 Delta 值就应该是-1。

2.Gamma（弯曲程度）

Gamma 主要用于描述你的投资组合价格曲线是不是弯了。对冲时，需要尽量使得对冲后的 Gamma 值接近于零（也就是案例 2 中将曲线拉成直线）。

3.Vega（隐含波动率）

一款条件完全相同的健康险，卖给 80 岁老年人的价格，必然远远高于卖给 20 岁年轻人的价格。其背后隐含的逻辑是，80 岁老人出现健康问题的概率，必然会远远高于 20 岁的年轻人。

因此，如果你想准确评估不同年龄段人群的健康风险发生概率，除了收集大量医疗数据进行统计分析外，更取巧的办法是，直接去市场中观察同一种健康险保单对不同人群制定的保费价格，保费越高则说明健康问题出现的概率越高。

这种由风险管理产品价格反映出的风险水平，便是该产品的隐含波动率。

如果将上文例子中的健康险保单换成期权产品，那么便可以通过直接观察同一期权产品市场价的高低，来间接判断价格在未来出现波动的概率。只要这是一个开放且自由竞争的有效市场，那么市场的价格发现职能便会自动反应出大家对未来价格波动率的共识。

而 Vega 便是反应期权价格对隐含波动率的敏感程度，因此我们只需要依托一些特定的算法，便可以轻易得出所有人对未来波动程度的预期。

Squeeth 产品与期权一样，都可以通过价格间接推导出未来价格的隐含波动率。而且其由于流动性的统一，必然使得其价格的博弈更加充分。因此相比于传统的期权产品，通过 Squeeth 求得的隐含波动率或许会更具代表性。