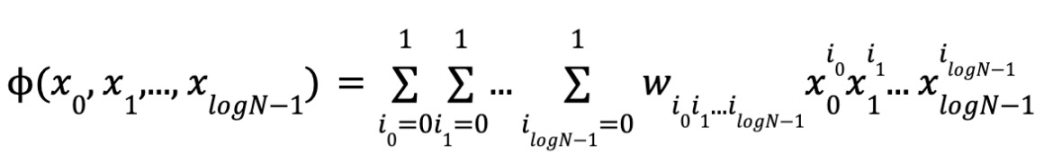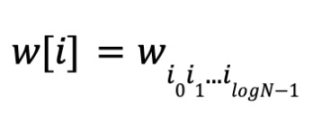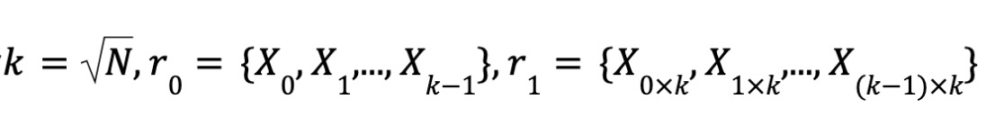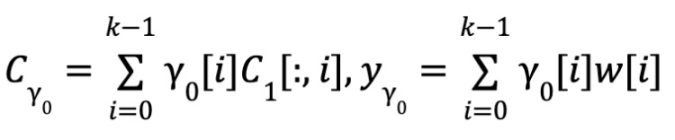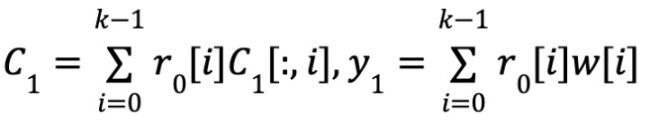撰文：康水跃，Fox Tech CEO；孟铉济，Fox Tech 首席科学家

在许多依赖多项式承诺的零知识证明系统当中，使用了不同的承诺协议。根据 a16z 的 Justin Thaler 在 2022 年 8 月文章「Measuring SNARK performance: Frontends, backends, and the future」的评估，Brakedown 虽然有较大的 Proof Size，但是无疑是当下最快的多项式承诺协议。

FRI、KZG、Bulletproof 是更为常见的多项式承诺协议，但速度是它们的瓶颈。zkSync 采用的 Plonky、Polygon zkEVM 采用的 Plonky2、Scroll 采用的 Ultra-Plonk 等算法都是基于 KZG 的多项式承诺。Prover 涉及到大量的 FFT 计算和 MSM 运算生成多项式和承诺，这两者都会带来大量的计算负担。 虽然 MSM 有运行多线程加速的潜力，但需要大量内存，即使在高并行下也很慢，而大型 FFT 则严重依赖算法运行时数据的频繁洗牌，难以通过分布式加速跨计算集群加载。

正是由于有了更为快速的多项式承诺协议 Brakedown，才使这类运算的复杂度大幅降低。

FOAKS 即 Fast Objective Argument of Knowledges，是由 Fox Tech 提出的一种基于 Brakedown 的零知识证明系统框架。FOAKS 在 Orion 的基础上进一步减少 FFT 运算，目标是最终消除 FFT。此外，FOAKS 还设计出一种全新的非常精妙的证明递归方式来减少证明大小。FOAKS 框架的优势在于在实现线性证明时间的基础上有着较小的证明大小，非常适合应用于 zkRollup 场景当中。

下文我们将详细介绍 FOAKS 所使用的多项式承诺协议 Brakedown。

在密码学当中，承诺（Commitment）协议由证明者（Prover）对某一个秘密值进行承诺，生成一个公开的承诺值，这个承诺值具有绑定性（Binding）和隐藏性（Hiding），之后提交者需要打开此承诺并将消息发送到验证者，以验证承诺与消息之间的对应关系。这一点，使得承诺协议和哈希函数的作用有许多共通之处，但是承诺协议往往依赖于公钥密码学领域的数学结构。而多项式承诺（Polynomial Commitment）是一类对于多项式的承诺方案，也就是说被承诺值是多项式。而同时多项式承诺协议当中还包含了在给定的点取值并给出证明的算法，这就使得多项式承诺协议本身成为一类重要的密码学协议，是许多零知识证明系统的核心部分。

而在最新的密码学领域的研究当中，由于发现了张量积（Tensor Product）和多项式取值之间的联系，所以诞生了一系列与此相关的多项式承诺协议，Brakedown 是其中的代表性协议。

在详细介绍 Brakedown 的协议细节之前，需要先了解一些基础知识。我们需要先了解线性码（Linear Code）、抗碰撞哈希函数（Hash Function）、默克尔树（Merkle Tree）、张量积（Tensor Product）的运算以及多项式取值的张量积表示。

首先是线性码（Linear Code）。一个消息长度为 k，码字长度为 n 的线性码是一个线性子空间

C∈Fn，使得存在一个从消息到码字的单射，称为编码，记作 EC：Fk→C。任意的对于码字的线性组合仍然是一个码字。两个码字 u，v 的距离即他们的汉明距离，记作△(u,v)。

最短距离为 d=minu,v△(u,v)。这样的码记作[n,k,d]线性码，用 d /n 表示码的相对距离。

其次是抗碰撞哈希函数（Hash Function）与默克尔树（Merkle Tree）。

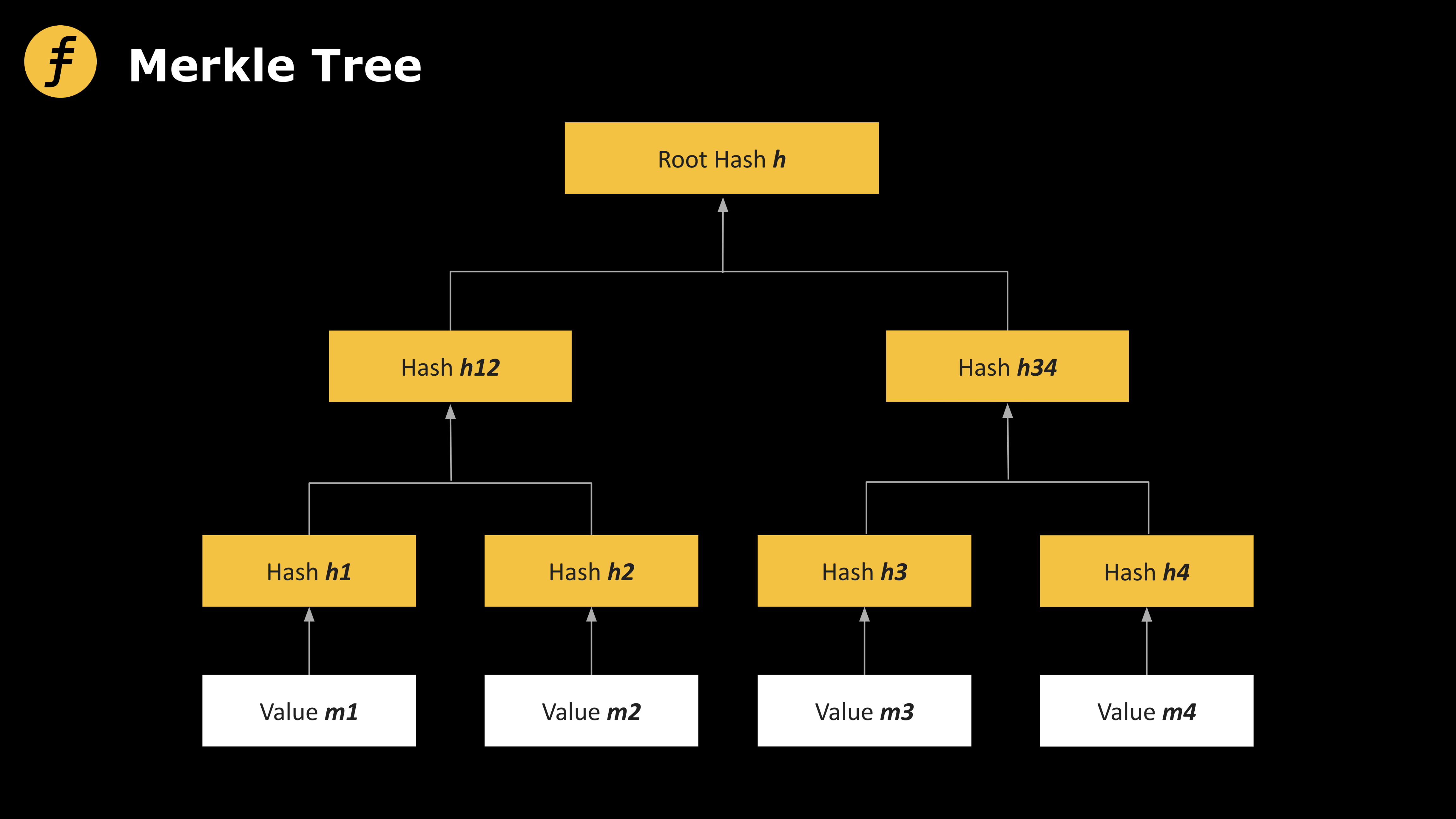
使用 H:{0,1}2λ→{0,1}λ表示一个哈希函数。默克尔树是一种特殊的数据结构，可以实现对于 2d个消息的承诺，生成一个哈希值 h，在打开任何消息时候需要 d+1 个哈希值。

默克尔树可以被表示为一个深度为 d 的二叉树，其中 L 个消息元素 m1,m2,...,ml分别对应树的叶子。树的每一个内部节点都由它的两个子节点进行哈希计算得出。打开消息 mi时，需要公开从 mi到根节点的路径。

用以下记号来表示：

  1. h←Merkle.Commit(m1,...,ml)
  2. (mi,πi)←Merkle.Open(m,i)
  3. {0,1}←Merkle.Verify(πi,mi,h)

深度解析FOAKS当中的多项式承诺协议Brakedown

图 1：默克尔树（Merkle Tree）

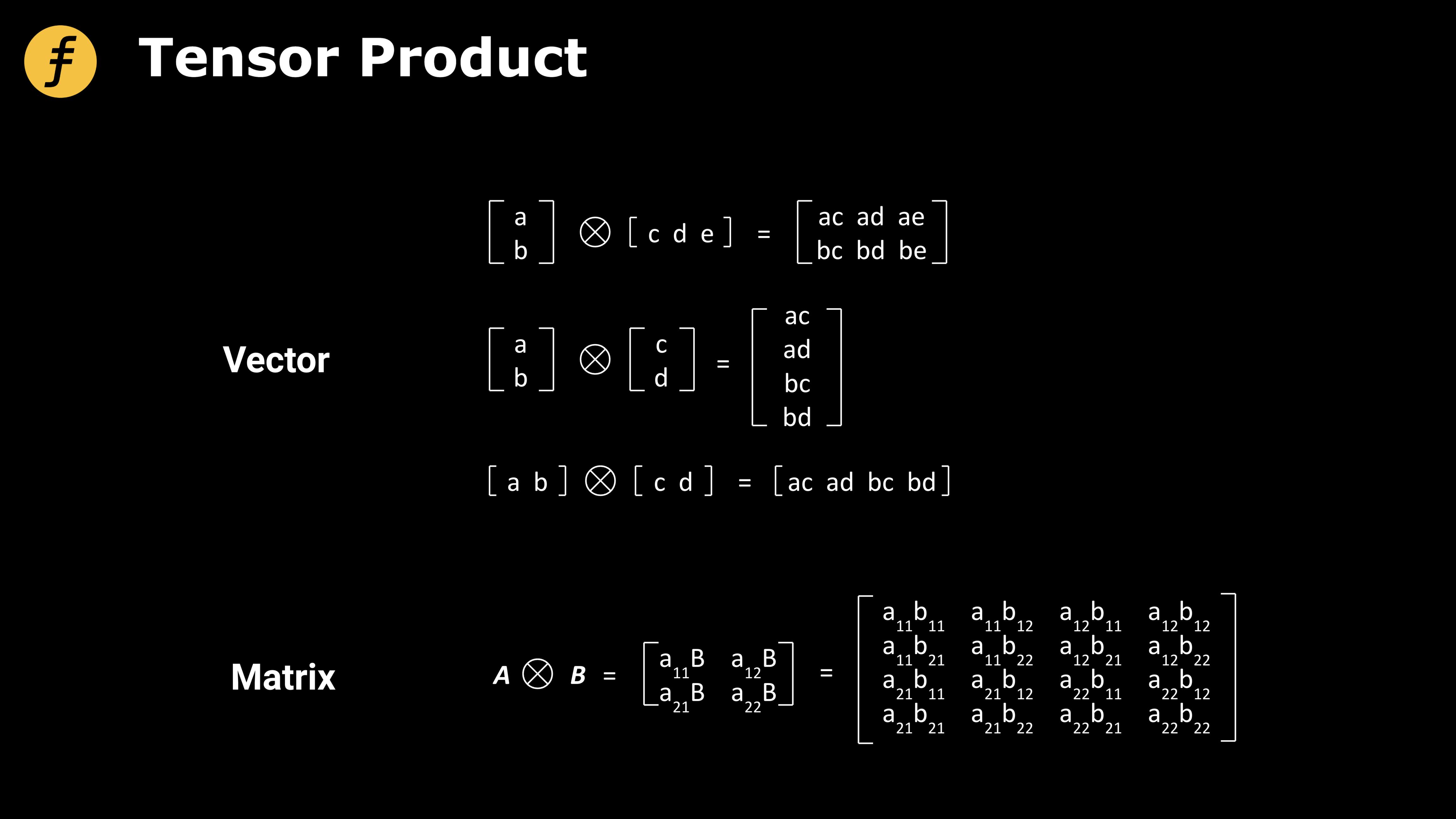
我们还需要了解张量积（Tensor Product）的运算是怎么做的。数学上，张量是向量和矩阵向高维空间的扩展，是很重要的研究对象，详细的讨论张量超出本文的研究范畴，这里只介绍向量和矩阵的张量积运算。

深度解析FOAKS当中的多项式承诺协议Brakedown

图 2：向量和矩阵的张量积运算

紧接着，我们需要知道多项式取值的张量积表示。

[GLS+]当中提到，多项式的取值可以被表示成张量积的形式。在这里我们考虑多线性多项式的承诺。

具体来讲，给定一个多项式，他在向量 x0,x1,...,xlogN-1的取值可以写成：

深度解析FOAKS当中的多项式承诺协议Brakedown

根据多线性的定义，每一个变量的次数是 0 或 1，因此，这里有 N 个单项式和系数，以及 logN 个变量。令 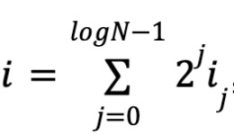深度解析FOAKS当中的多项式承诺协议Brakedown，其中 i0i1...ilogN-1是 i 的二进制表示。令 w 表示多项式系数，深度解析FOAKS当中的多项式承诺协议Brakedown

。同样的，定义 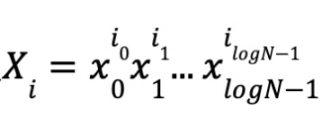深度解析FOAKS当中的多项式承诺协议Brakedown 。令

深度解析FOAKS当中的多项式承诺协议Brakedown

于是有 X=r0⊗r1。

从而，多项式取值可以被表示成张量积的形式：ϕ(x0,x1,...,xlogN-1)=

最后，我们来看 FOAKS、Orion[XZS22]当中使用的 Brakedown 的过程。

首先，PC.Commit 将多项式系数 w 划分成 k×k 的矩阵形式，并将其编码（参考「预备知识」中的线性码），记作 C2。之后对于 C2的每一列 C2[:,i]进行承诺建立一个默克尔树，然后再对于每一个列形成的默克尔树树根建立另一个默克尔树，作为最终的承诺。

在取值证明的计算中，需要证明两点，一是近似性（Proximity），二是一致性（Consistency）。近似性保证了承诺的矩阵确实和编码后的一个码字足够接近。一致性保证 y=

近似性检验：近似性检验由两步组成。首先，验证者发送一个随机向量 0 给证明者，证明者计算 Y0与 C1的内积，也就是以 Y0的分量为系数对 C1的行计算线性组合。由于线性码的性质，Cy0是 Yy0的码字。之后，证明者证明 Cy0确实是从被承诺的码字计算出的。为了证明这一点，验证者随机选取 t 列，证明者打开对应的列并提供默克尔树证明。验证者检查这些列和 Y0的内积和 Cy0当中对应位置相等。[BCG20]当中证明如果使用的线性码有常数的相对距离，那么被承诺的矩阵就以压倒性的概率与一个码字接近（压倒性的概率是指，命题的否命题成立的概率是可忽略的）。

一致性检验：一致性检验和近似性检验的流程完全类似。不同之处在于，不使用随机向量 Y0而是直接使用 r0来完成线性组合的部分。类似的，c1也是消息 y1的一个线性码，并且有

ϕ(x)=。[BCG20]当中证明，通过一致性检验，如果被承诺的矩阵与一个码字接近，则以压倒性概率成立 y=ϕ(x)。

以伪代码形式，我们给出 Brakedown 协议的流程：

Public input：The evaluation point X，parsed as a tensor product X=r0⊗r1;

Private input：The polynomial ϕ ，the coefficient of is denoted by w.

Let C be the [n,k,d]-limear code，EC：FkFn be the encoding function，N=k×k. If N is not a perfect square，we can pad it to the next perfect square. We use a python style notationmat[:,i] to select the i-th column of a matrix mat。

  1. function PC. Commit(ϕ)：
  2. Parse w as a k×k matrix. The prover locally computes the tensor code encoding C1，C2 ，C1 is a k×n matrix，C2 is a n×n matrix.
  3. for i∈ [n] do
  4. Compute the Merkle tree root Roott=Merkle.Commit(C2[:,i])
  5. Compute a Merkle tree root R=Merkle.Commit([Root0,......Rootn-1]),and output R as the commitment.
  6. function PC. Prover(ϕ, X, R)
  7. The prover receives a random vector Y0∈Fk from the verifier
  8. Proximity 深度解析FOAKS当中的多项式承诺协议Brakedown
  9. Consistency 深度解析FOAKS当中的多项式承诺协议Brakedown
  10. Prover sends C1,y1,C0,y0 to the verifier.
  11. Verifier randomly samples t[n] as an array Î and send it to prover
  12. for idx∈Î do
  13. Prover sends C1 [:,idx] and the Merkle tree proof of Rootidx for C2 [:,idx] under R to verifier
  14. function PC. VERIFY_EVAL(πX,X,y=ϕ(X),R)
  15. Proximity: ∀idx∈Î,CY0[idx]==and EC(Yy0)==CY0
  16. Consistency:∀idx∈Î,C1[idx]==and EC(Y1)==C1
  17. y==
  18. ∀idx∈Î, EC(C1[:,idx]) is consistent with ROOTidx, and ROOTidx’s Merkle tree proof is valid.
  19. Output accept if all conditions above holds. Otherwise output reject.

结语：多项式承诺是一类非常重要的密码学协议，被广泛的应用在许多密码学系统当中，尤其是零知识证明系统。本文详细介绍了多项式承诺 Brakedown 协议以及和其相关的数学知识，作为 FOAKS 很重要的底层组件，Brakedown 对 FOAKS 的实例化性能的提升起到了重要作用。

参考文献

[GLS+]:Alexander Golovnev, Jonathan Lee, Srinath Setty, Justin Thaler, and Riad S. Wahby. Brakedown: Linear-time and post-quantum snarks for r1cs. Cryptology ePrint Archive. https://ia.cr/2021/1043.

[XZS22]:Xie T, Zhang Y, Song D. Orion: Zero knowledge proof with linear prover time[C]//Advances in Cryptology–

CRYPTO 2022: 42nd Annual International Cryptology Conference, CRYPTO 2022, Santa Barbara, CA, USA, August 15–18, 2022, Proceedings, Part IV. Cham: Springer Nature Switzerland, 2022: 299-328.https://eprint.iacr.org/2022/1010

[BCG20]:Bootle, Jonathan, Alessandro Chiesa, and Jens Groth. "Linear-time arguments with sublinear verification from tensor codes." Theory of Cryptography: 18th International Conference, TCC 2020, Durham, NC, USA, November 16–19, 2020, Proceedings, Part II 18. Springer International Publishing, 2020.

Justin Thaler from A16zcrypto, Measuring SNARK performance: Frontends, backends, and the future

https://a16zcrypto.com/measuring-snark-performance-frontends-backends-and-the-future/

张量积的介绍：https://blog.csdn.net/chenxy_bwave/article/details/127288938