PART4.Modelling

协整
实际上,很难找到一种具有均值回归行为的可交易资产。股票的总体表现类似于GBM,因此,均值回归交易策略相对无用。然而,没有什么能阻止我们创建一个平稳的价格序列投资组合。因此,我们可以将均值回归交易策略应用于投资组合。
均值回归交易策略的最简单形式是经典的“配对交易”,通常涉及美元中性的多/空股票对。该理论认为,同一行业的两家公司很可能受到影响其业务的类似市场因素的影响。偶尔,它们的相对股价会因某些事件而出现背离,但会回归长期均值。
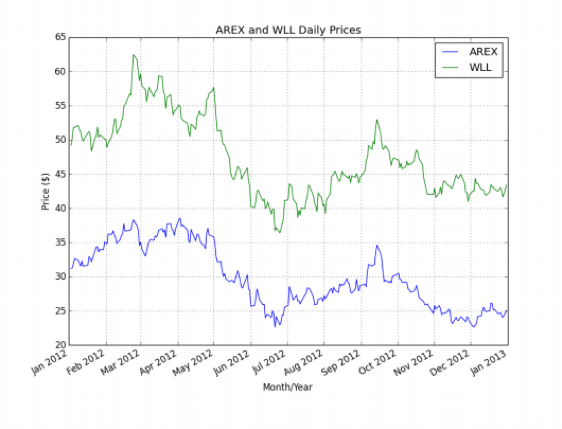
让我们考虑两家能源股公司,分别是股票代码为AREX的资源公司(Resources Inc)和股票代码为WLL的惠廷石油公司(Whiting Petroleum Corp)。两者都处于相似的市场环境中,因此很可能存在平稳的配对关系。现在我们将创建一些图形,使用pandas和Matplotlib库来演示AREX和WLL的协整特性。第一个图(图10.1)显示了2012年1月1日至2013年1月1日期间它们各自的价格历史。
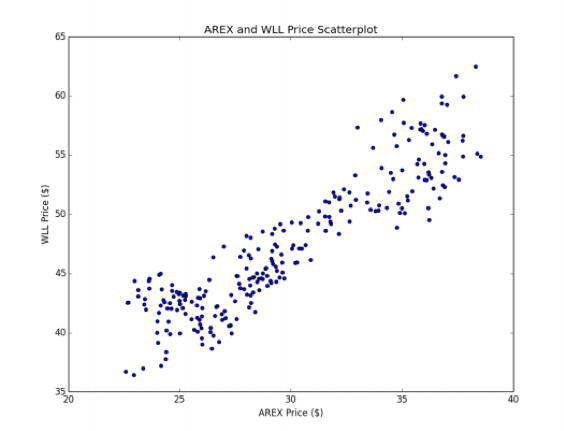
如果我们创建它们价格的散点图,我们可以看到这段时期的关系大致是线性的(见图10.2)。这组股票的交易本质上是通过一个线性模型来处理两种股票价格之间的关系:

其中y(t)是AREX股票的价格,x(t)是WLL股票的价格,都在第t天。
如果我们画出残差 (为特定值的β将在下方决定)我们创建一个新的时间序列,乍一看,看起来相对固定。这在图10.3中给出。
我们将在下面描述每个图的代码。

协整增广Dickey-Fuller检验-为了在统计上确认这个级数是否均值回归,我们可以使用上面描述的其中一个测试,即增广的Dickey-Fuller测试或Hurst指数。然而,这些测试会帮助我们确定β,套期保值比率需要形成线性组合,他们只会告诉我们关于一个特定β,线性组合是否稳定。
这就是协整增广Dickey-Fuller (CADF)测试的作用。通过对两个时间序列进行线性回归,确定最优套期保值比率,并对线性组合下的平稳性进行检验。
Python实现-现在,我们将使用Python库测试AREX和WLL之间在2012年1月1日到2013年1月1日期间的协整关系。我们将使用Yahoo Finance作为数据源和statsmodel进行ADF测试,如上所述。
第一个任务是创建一个新文件cadf。,并导入必要的库。该代码使用了NumPy、Matplotlib、panda和statsmodel。为了正确标记坐标轴并通过panda从Yahoo Finance下载数据,我们导入了matplotlib。日期模块和http://pandas.io。数据模块。我们还利用了pandas的普通最小二乘(OLS)函数:
#!/usr/bin/python
# -*- coding: utf-8 -*-
# cadf.py
import datetime
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import pandas as pd
import pandas.io.data as web
import pprint
import statsmodels.tsa.stattools as ts
from pandas.stats.api import ols 第一个函数plot_price_series接受pandas Dataframe作为输入,其列由占位符字符串“ts1”和“ts2”给出。这些将是我们的配对股票。该函数简单地将两个价格序列绘制在同一个图表上。这使我们可以直观地检查是否可能进行任何协整。
我们使用Matplotlib date模块从datetime对象获取月份。然后我们创建一个图形和一组轴,用于应用标签/绘图。最后,绘制图:
# cadf.py
def plot_price_series(df, ts1, ts2):
months = mdates.MonthLocator() # every month
fig, ax = plt.subplots()
ax.plot(df.index, df[ts1], label=ts1)94
ax.plot(df.index, df[ts2], label=ts2)
ax.xaxis.set_major_locator(months)
ax.xaxis.set_major_formatter(mdates.DateFormatter(’%b %Y’))
ax.set_xlim(datetime.datetime(2012, 1, 1), datetime.datetime(2013, 1, 1))
ax.grid(True)
fig.autofmt_xdate()
plt.xlabel(’Month/Year’)
plt.ylabel(’Price ($)’)
plt.title(’%s and %s Daily Prices’ % (ts1, ts2))
plt.legend()
plt.show() 第二个函数plot_scatter_series绘制了两个价格的散点图。这让我们可以直观地检查两个系列之间是否存在线性关系,从而判断它是否适合OLS过程和随后的ADF测试:
# cadf.py
def plot_scatter_series(df, ts1, ts2):
plt.xlabel(’%s Price ($)’ % ts1)
plt.ylabel(’%s Price ($)’ % ts2)
plt.title(’%s and %s Price Scatterplot’ % (ts1, ts2))
plt.scatter(df[ts1], df[ts2])
plt.show() 第三个函数plot_residuals用于绘制两个价格序列的拟合线性模型的残差值。该函数要求panda DataFrame有一个“res”列,表示剩余价格:
# cadf.py
def plot_residuals(df):
months = mdates.MonthLocator() # every month
fig, ax = plt.subplots()
ax.plot(df.index, df["res"], label="Residuals")
ax.xaxis.set_major_locator(months)
ax.xaxis.set_major_formatter(mdates.DateFormatter(’%b %Y’))
ax.set_xlim(datetime.datetime(2012, 1, 1), datetime.datetime(2013, 1, 1))
ax.grid(True)
fig.autofmt_xdate()
plt.xlabel(’Month/Year’)
plt.ylabel(’Price ($)’)
plt.title(’Residual Plot’)
plt.legend()
plt.plot(df["res"])
plt.show() 最后,该过程被封装在一个__main__函数中。第一个任务是从Yahoo Finance下载AREX和WLL的OHLCV数据。然后,我们创建一个单独的DataFrame df,使用与AREX框架相同的索引来存储这两个调整后的收盘价。然后绘制价格序列和散点图。
绘图完成后,通过调用WLL和AREX系列上的pandas ols函数计算残差。这使我们能够计算β对冲比率。然后,通过形成WLL和AREX的线性组合,利用对冲比率创建一个“res”列。
最后绘制残差图,并对计算出的残差进行ADF检验。然后打印ADF测试结果:
# cadf.py
if __name__ == "__main__":
start = datetime.datetime(2012, 1, 1)
end = datetime.datetime(2013, 1, 1)
arex = web.DataReader("AREX", "yahoo", start, end)
wll = web.DataReader("WLL", "yahoo", start, end)
df = pd.DataFrame(index=arex.index)
df["AREX"] = arex["Adj Close"]
df["WLL"] = wll["Adj Close"]
# 绘制两个时间序列
plot_price_series(df, "AREX", "WLL")
# 显示两个时间序列的散点图
plot_scatter_series(df, "AREX", "WLL")
# 计算最优对冲比率“贝塔”
res = ols(y=df[’WLL’], x=df["AREX"])
beta_hr = res.beta.x
# Calculate the residuals of the linear combination
df["res"] = df["WLL"] - beta_hr*df["AREX"]
# 计算线性组合的残差
plot_residuals(df)
# 计算并输出残差的CADF测试
cadf = ts.adfuller(df["res"])
pprint.pprint(cadf) 代码的输出如下:
(-2.9607012342275936,
0.038730981052330332,
0,
249,
{’1%’: -3.4568881317725864,
’10%’: -2.5729936189738876,
’5%’: -2.8732185133016057},
601.96849256295991) 可以看出,-2.96的计算检验统计量小于-2.87的5%临界值,这意味着我们可以拒绝在5%水平上不存在协整关系的原假设。因此,我们可以合理肯定地得出AREX和WLL至少在考虑的时间段样本上具有协整关系。
我们将在后面的章节中使用这对组合来创建一个实际的交易策略,使用一个实现的事件驱动的回溯测试系统。
更多内容请关注公众号【火象】~













