
We know the past but cannot control it.
We control the future but cannot know it.
——Claude Shannon
公元前3500年,在美索不达米亚平原的乌鲁克城,诞生了人类最早的文字,这也是后来楔形文字的起源,流行歌曲《爱在西元前》的歌词中这样写道:
我给你的爱写在西元前,深埋在美索不达米亚平原,
几十个世纪后出土发现,泥板上的字迹依然清晰可见,
我给你的爱写在西元前,深埋在美索不达米亚平原,
用楔形文字刻下了永远,那已风化千年的誓言,一切又重演。”
那是最古老的文明之一,幼发拉底河、底格里斯河缓缓流淌,乌鲁克,乌尔,基什,拉格什,众多璀璨的城邦在新月沃地星罗棋布,英雄王吉尔伽美什谱写出那个时代最壮美的史诗,并将人类社会推向了一个崭新的篇章。

而美好总是转瞬即逝的,当历史走过数千年,从亚述、巴比伦,到波斯、马其顿,再到伊拉克、叙利亚,无数的人民、奇迹都归于尘土,胜者加冕为王,败者前赴后继,在不断的循环中,大多数存在都成为历史中被忽略的一瞬,但是早期文明开拓未知的精神却可以穿越时空得以保留,我们到今天仍然可以追忆缅怀千年之前苏美尔的灿烂和繁荣。
物质终将消散,而信息可以永存。当我们探索元宇宙时,无法避开地会去思考信息到底是什么?为什么元宇宙中的信息让如此多的当世豪杰趋之若鹜?在这篇文章里,我们将探讨信息的本质以及人类在创造信息、传播信息领域的漫漫征途。
“信息”一词在古希腊文中的词源是εἶδος,用来表示“事物的本质”。我们看到一个苹果时,可以得到红色、圆形、固体等各种描述性的信息,大脑通过处理这些信息,我们知道了这是一个苹果。信息在我们的日常生活中随处可见,一则消息,一条动态,一段视频,都包含着不同的信息,但我们即便在我们朴素的认知里,也很清楚信息和物质并不是相同的,相同的物体在不同的时间可以传达出不同的信息,而不同的物体也可以承载部分相同的信息。如果不是物质,那么信息是什么?

信息的定义
爱因斯坦著名的质能方程告诉我们能量和物质是可以相互转换的(注:实际上是“能量和质量可以相互转换”,在不影响结论的前提下,为了方便叙述,我们用“物质”代替“质量”,并不完全严谨),直觉告诉我们,物质是可以被感知到的真实存在的,而能量更像是一种抽象的性质,看不见摸不着,只能通过某些相关性质来感受,如温度、速度等,而事实并非如此。狭义相对论给出的结论恰恰相反,静止的物体依旧拥有能量,而在物质的转化过程中,能量是守恒的,可见能量才是本质,物质只是能量的量度和载体,能量需要依托于物质而存在,而没有能量也就没有所谓的物质了。能量与物质便是本质与载体的关系,我们也可以以类似的方式来理解信息。

当我们写下文字,拍下照片,信息便被记录在相应的载体之中,如果没有这些物质载体的话,信息就无法保存、传递,显而易见,物质也是信息的载体。反过来想,不包含信息的物质是什么?集合论的公理告诉我们,空集也是集合且是所有集合的子集,类比思考,“没有信息”本身也是一种信息,一串无限循环的0并不是无信息,而是代表了“无”这一信息,因此物质不可能不包含信息。

信息并非物质,却可以描述物质的性质,这种模糊的概念尽管方便理解,但并不能帮助我们洞悉信息的本质。从科学研究的角度出发,信息需要更加明确且可以量化的定义,于是信息论的鼻祖、现代信息学科的总奠基人——香农给出了最优雅的定义。
Information is the resolution of uncertainty.
信息是用来消除不确定性的。

信息的数学本质
不确定性很容易理解,我们的生活中就充斥着各种不确定性,大到天气的变化,股市的波动,小到回家的时间,晚饭的选择,随机事件构成了这个世界的全部,而不确定性的量化方式便是概率。
当一个事件中各个结果发生的概率越低,也就意味着不确定越大,说明可能发生的事情也就越多,那么信息量也就更大;反过来说,当一个事件中各个事件发生的概率越高,也就意味着不确定越小,说明可能发生的事情也就越少,那么信息量也就更小。举例来说,一个骰子可以产生六种可能结果,一枚硬币可以产生两种可能结果,那么显然骰子所能提供的信息量显然多于硬币。简单来说,信息量与概率大小是成反比的,而信息就是剔除掉无用部分,让总信息量减少并降低不确定性的存在。

将随机排列的数字按顺序整理好,这就是信息;将声音以一定规律传播出去,这就是信息;将无数的想法整理成书籍,这就是信息;把混杂的信号去除掉噪音,这就是信息。
非常反直觉的一点在于,当我们获取的知识信息越来越多的时候,不确定性难道是增大了么?对,也不对。从整体角度来说,我们所拥有的信息总量越发庞大,面对具体场景能抽取出来的有效信息的可能性也就越低,这个角度来看不确定性确实增加了。但是得益于大脑的信息处理能力,知识总量越多,知识之间建立起来的关联也就越精准,抽取有效信息的能力反而变强了,对于个体来说也更稳定了。

1928年,哈特莱率先提出了将信息量化的方式,当信源有m种消息且所有消息的概率相等时,该信源的信息量可以表示为
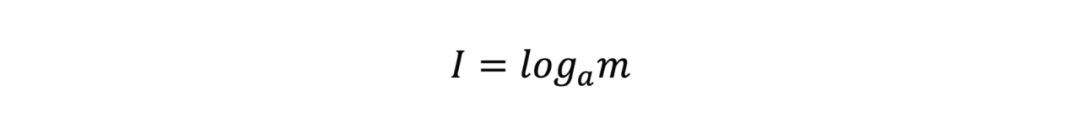
关于a的选择并没有要求,a的改变只相当于在公式前乘以一个常系数。在这一量化方式提出的时候,十进制还是主流,a一般被设定为10,后来随着电子信息技术的发展,二进制成为了信息的主要表达媒介,a也就被调整成了2。
以2为底的话,当我们抛出一枚硬币,信息量就是
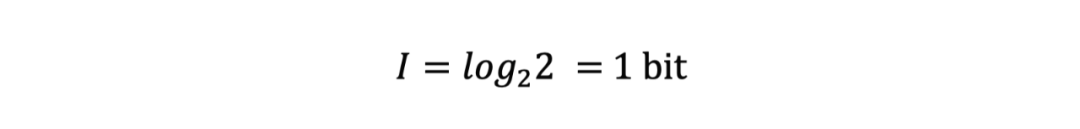
当抛出两枚硬币时,信息量就是
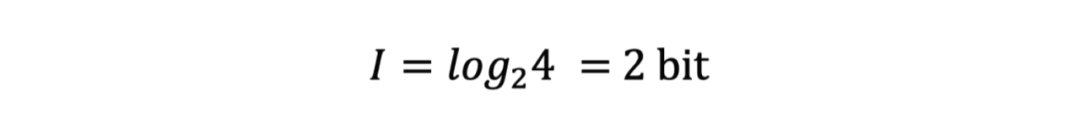
对于大多数人来说,对数并不容易理解,但是选择对数并不是为了增加难度,而是有意为之的,这里就要给出关于信息的几种性质,我们把x作为一次事件,用H(x)来表示x事件的信息量,用p(x)来表示事件发生的概率,那么

第一条性质非常显然,信息量必然是非负的;前文中,我们也指出概率越低,不确定性便越高,信息量也就越大,第二条性质也是容易理解的。
但是非负且递减的函数太多了,当然没必要是对数,这里第三条性质就显得很重要了。当x和y是两个不相关的事件时,两个事件同时发生的信息总量应该是两个事件独立发生的信息量之和,也就是H(x,y)=H(x)+H(y);根据独立事件概率公式,两个独立事件同时发生的概率是两个事件各自发生之积,那么就有p(x,y)=p(x)p(y)。
另外,根据之前的讨论,信息量应该只由时间发生的概率来决定,那么也就有H(x,y)=H(p(x),p(y))=H(p(x))+H(p(y)),到这里,根据经验,我们就可以得到信息量的公式
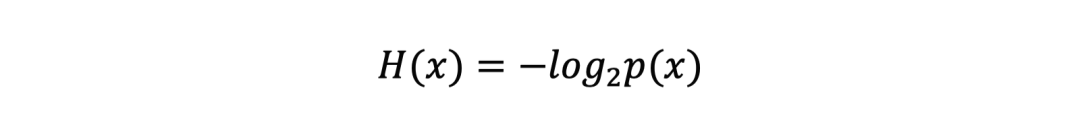
注意到p(x)始终在0到1之间,那么很容易就可以验证,H(x)满足上述三条性质,那么信息量的公式也就基本获得了。
有些人会困惑,这个公式是猜出来的,可能还有其他满足条件的公式,答案当然是否定的,后续我们会给出相关证明。
信息熵
写到这里,我们终于可以引入信息熵了,这是信息论的基石,是人类踏入信息时代的开端,是一切现代电子信息技术的核心底层原理,当然也包括元宇宙。
1948年10月,年仅32岁的香农在《贝尔系统技术学报》上发表了现代信息论的奠基之作,《A Mathematical Theory of Communication》,短短55页,从数学角度严谨地定义了信息量以及诸多衍生性质。相隔200余年,与牛顿爵士的那部《Mathematical Principles of Natural Philosophy》交相辉映,各自谱写了科学史上最华丽的篇章之一,我们愿意相信,天才尽管少见却真的存在,英雄会消逝,但人类的智慧确实会得到传承。

说回信息熵,香农认为信息量度量了一个事件所包含的信息的多少,而信息熵则代表了所有可能发生的事件的信息量的数学期望。与之前的性质类似,信息熵也需要满足三条性质:
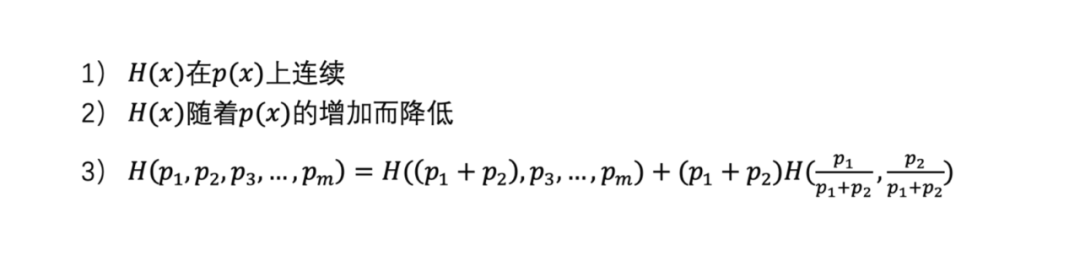
前两条无需赘述,关于第三条性质,将一个随机实验分成两部分,划分前的总信息熵等于划分之后的各部分信息熵的加权和,可以理解成总分支的信息熵是不变的,但是具体分支的信息熵要乘以对应的系数,因为分支的发生是有一定概率的。
在上述三个条件的约束下,我们便得到了本篇文章最为重要的公式,简洁而优美的信息熵,
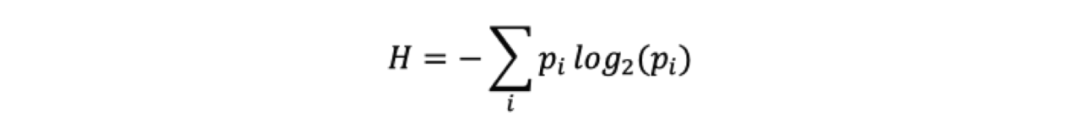
自此,信息得到了严格的量化,并且和概率建立起了直接的关系,贝叶斯定理中的大量结论都可以无缝应用到信息论中,电子信息也来到了字节的时代。
信息熵公式的推导
我们检验可以得知,信息熵公式满足上述三种性质,当然但这并不能证明信息熵公式的唯一性,或许还有其他满足的公式?为什么一定要是一个奇怪的对数式?伟大的克劳德·香农当然不会不知道这一点,在论文中也给出了对于唯一性的严格证明,我们也可以借此一窥天才们扎实的数学功底。

给定一个事件x,不妨假设该事件所有结果发生的概率均为,记
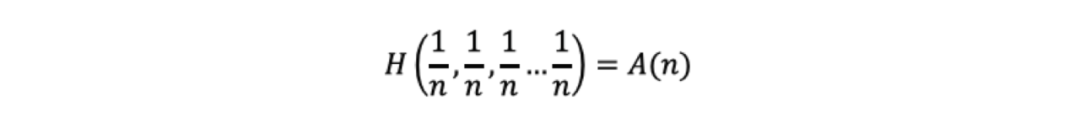
根据第三条性质,我们可以得到,从s^m种可能性中得到一种的信息量,相当于从s种可能性中得到m种的信息量,那么就可以得到:
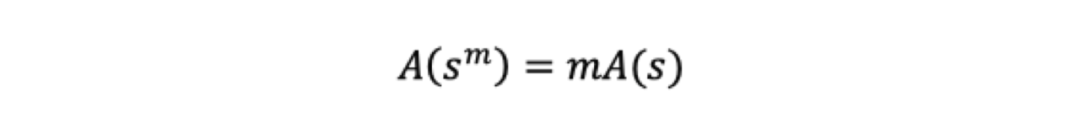
相似的,我们也可以得到:
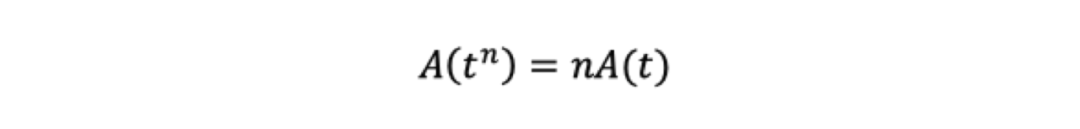
对于任意n,我们都能找到一个m,使得
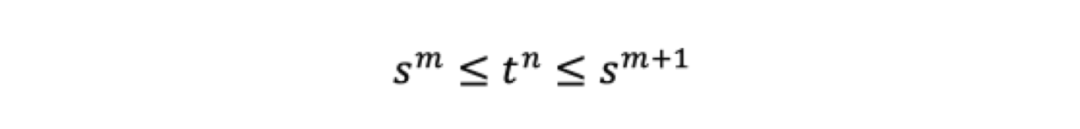
我们对上式取对数然后除以nlogs得到
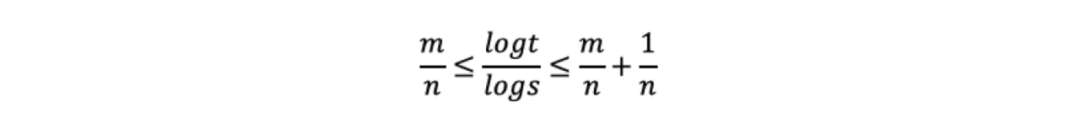
那么可以得到对于任意ε>0,都有
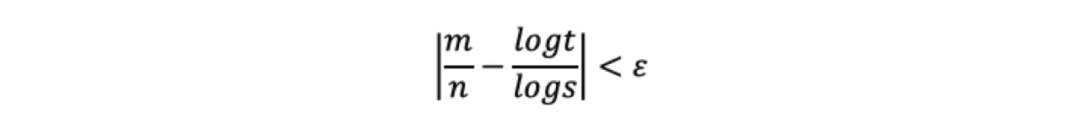
根据单调性可以得到
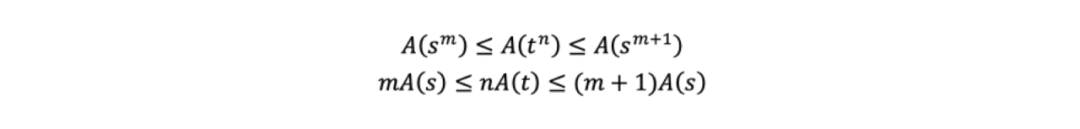
同时除以nA(s),
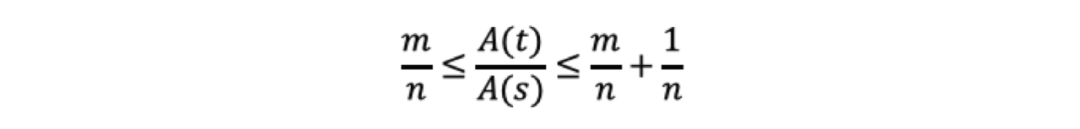
那么可以得到对于任意ε>0,都有

也就有
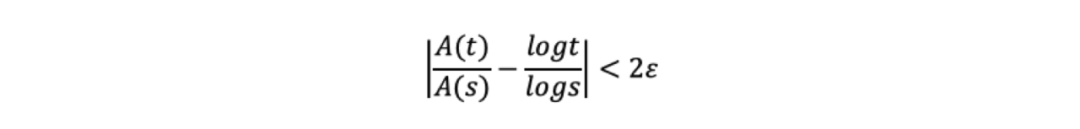
显然
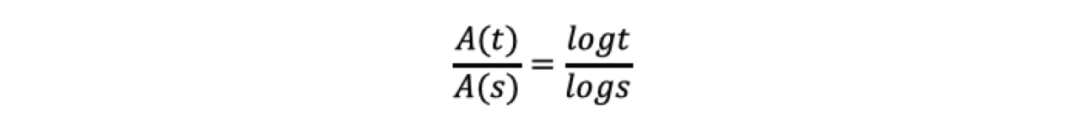
根据t和s的一般性,我们自然就会得到
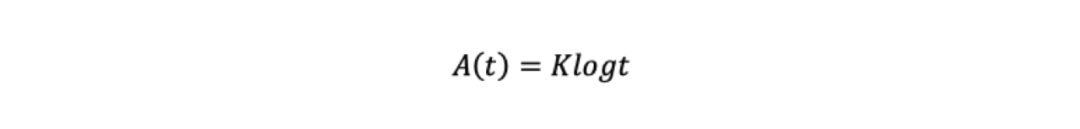
其中K>0。
接下来根据性质三,我们假定一个随机实验,令t=n1+n2+...+ni,也就是共有n1+n2+...+ni个等概率可能性,令pi=ni/(n1+n2+...+ni),将这个随机实验分成两部分,第一部分是从n1+n2+...+ni个结果中选择种ni可能性;第二部分是将这次实验拆分成i个实验,当i选定之后,从ni个等概率结果中选择一种可能性,那么我们也就有,

那么,
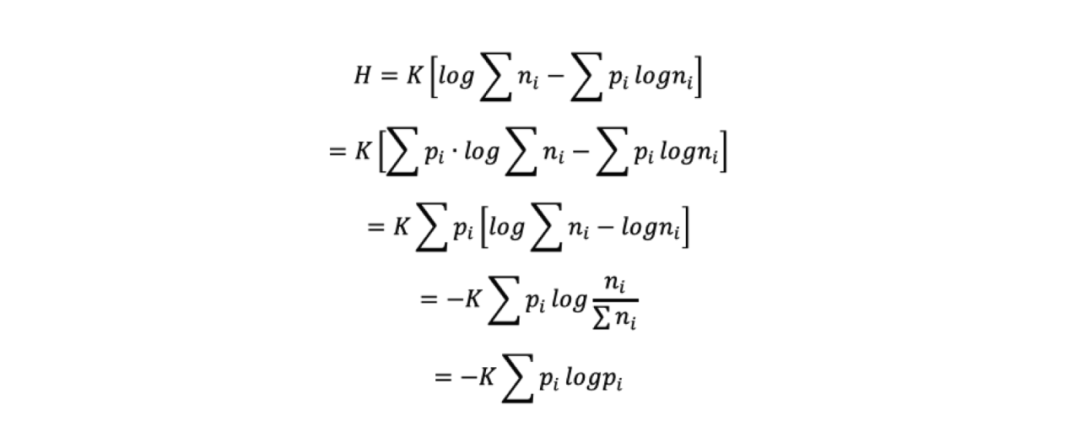
K作为常数,为了方便计算,可以根据具体用途可以选择相应的数值。
至此,我们通过严格的推导获得了信息熵公式,并没有用到很高深的数学知识,过程足够优美,这也给整个信息学科定下了优雅的调性。
文明即熵减
熵是一个伟大的概念,在物理学里,熵是系统混乱程度的量度,毫无疑问香农借鉴了这一定义,并引入到了信息学科当中。
熵最早由克劳修斯在1865年提出,当时只是作为一个热力学概念,表示热量相对于温度的变化率,彼时熵的定量计算还并不重要,更多是用来描述可逆系统的状态变化。这里我们不对可逆系统做详细讨论,但需要给出一个最重要的关于熵的结论,热力学第二定律。

在不同语境下,热力学第二定律有不同的表述。
比如,最易于理解的表述,热量总是从高温物体传递到低温物体,不可能做反向传递且并不引起其他变化;
比如,热力学的表述,功可以全部转化为热,但热不能全部转化成功;
比如,关于熵的表述,孤立系统总是自发向着熵增的方向变化。
对于热力学第二定律我们暂且按下,1877年,玻尔兹曼从统计力学的角度给出了熵的定义式
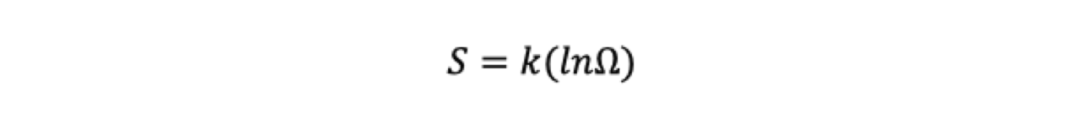
其中表示微观粒子的状态数量。对于状态数量我们可以这样理解,假设一组10枚硬币,如果10枚硬币都是正面,那么只有1种组合方式,如果5枚正面5枚反面,那么便有5C10=252种组合方式。不难看出,可以看作系统混乱程度的度量,越有规律的系统越小,反之相反。

我们再来重看热力学第二定律,高温物体和热量代表着更混乱的系统,低温物体和功代表着更有序的系统,而孤立系统总是自发地向着更混乱的状态变化,当我们不清理街道,城市就会越来越乱,当我们没有秩序,社会便会变成一团散沙。
玻尔兹曼给出的熵公式和香农的信息熵如出一辙,信息是消除不确定性的存在,因为有了有序的信息,混乱度才会下降,熵才得以降低。孤立系统总是自发地熵增,但正是因为人类创造了秩序,整理了信息,使得我们的系统实现了熵减,因此也诞生了文明。
















