本文作者是Mechanism Capital 研究员Benjamin Simon,本文通过AMPL和Basis实例分析了算法稳定币面临的问题以及算法稳定币的优点。作者认为算法稳定币是一种有吸引力的货币实验,在此早期阶段关闭算法稳定币将是愚蠢的,但其风险也不能被忽视。
2014年,两篇学术论文正式发布:一篇是由费迪南多·阿梅特拉诺(Ferdinando Ametrano)编写的《Hayek Money:加密货币价格稳定解决方案》,另一篇是由罗伯特·萨姆斯(Robert Sams)编写的》关于加密货币稳定性的注意事项:铸币税股份》。
借鉴弗里德里希·哈耶克(Friedrich Hayek)对黄金标准的批评,阿梅特拉诺(Ametrano)认为,由于通缩性,比特币无法充分执行我们要求的货币单位制。取而代之的是,他提出了一种基于规则的,供应弹性的加密货币,可以根据需求进行``调整""(即改变所有代币持有者在货币供应中占的比例)。
萨姆斯(Sams)在《铸币税股份》文中提出了一种具有相似理由的相似模型,但有一个重要的转折。Sams的系统取代了在所有钱包中按比例分配货币供应量的“基础”货币,而是由两个代币组成:这种供应弹性的货币本身和在网络中的投资“份额”。后者资产的所有者(Sams称其为“铸币税股份”)是正向供应增加带来的通货膨胀收益的唯一接受者,而当货币需求下降且网络收缩时则是债务负担的唯一承担者。
精明的加密货币观察家将认识到Ametrano的《Hayek Money》和Sams的《铸币税股份》不再是学术抽象。《Hayek Money》几乎就是现在的Ampleforth,后者于2019年推出,并于2020年7月猛增至市值超过10亿美元。最近,萨姆斯(Sams)的《铸币税份额》模型在不同程度上为Basis,Empty Set Dollar,Basis Cash和Frax等算法稳定币奠定了基础。
现在摆在我们面前的问题与六年前Ametrano和Sams论文的读者面临问题没有什么不同:算法稳定币能否真正实现长期生存能力?算法稳定币会一直受到极端的扩张和收缩周期影响吗?哪种算法的稳定币更引人注目:一个简单的基础模型或一个多代币的“铸币税”系统(或完全其他的东西)?
在所有这些问题上,都仍未解决,可能需要一段时间才能达成广泛共识。尽管如此,本文还是试图从第一性原理的推理以及最近几个月的一些经验数据中探究其中一些基本问题。
1
稳定币背景
算法稳定币本身就是一个世界,但是在深入研究之前,值得退后一步,调查一下更广泛的稳定币前景。(已经熟悉稳定币的读者可以略过或跳过本节。)
由于比特币的机构采用滚雪球般地向前发展,DeFi夏季热潮以及以太坊即将进行的网络升级,稳定币近来让人惊讶不已,总市值已超过250亿美元。这种抛物线式的增长吸引了密码学界以外的强大个体的眼球,其中包括最近一批美国立法者。
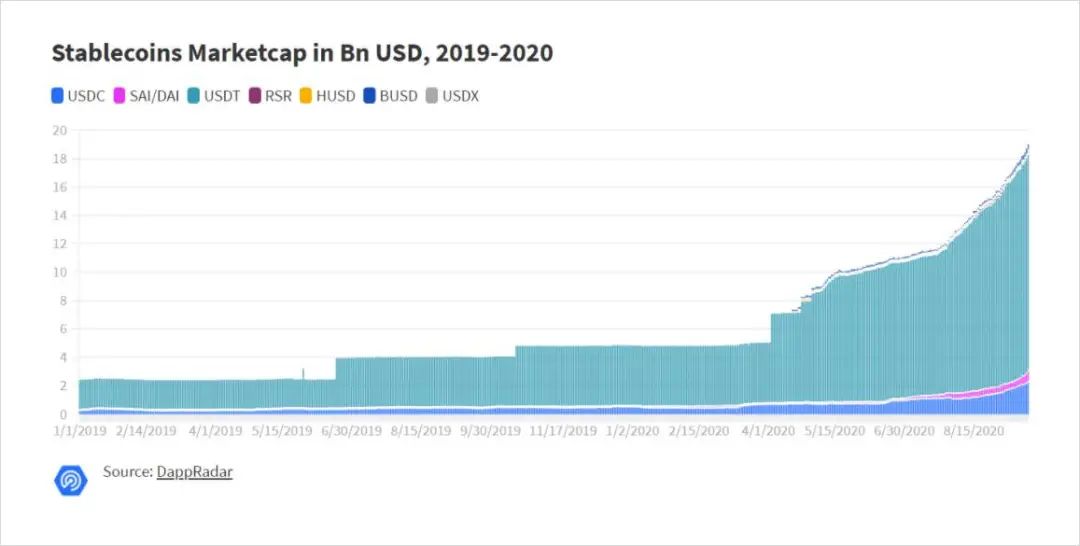
USDT仍然是主要的稳定币,但它远非唯一的稳定币。广义上讲,我们可以将稳定币分为三类:美元抵押型,多资产池过度抵押型和算法型(1)。我们在本文中的重点是最后一个类别。但是,重要的是要注意稳定币在其他类别中的优缺点,因为理解这些折衷方案将使我们能够提高算法稳定币的价值主张。
第一类稳定币(即USDT和USDC,但也包括基于交易所的代币(平台币),如BUSD)由中心化管理的,由美元提供支撑并且1:1可赎回。这些稳定币具有一种受到保证的挂钩和资本高效的优点(即没有过度抵押),但是它们的中心化性质意味着用户可以被列入黑名单,而挂钩本身取决于中央实体的可信赖行为。
第二类是多资产抵押稳定币,包括MakerDAO的DAI和Synthetix的sUSD。这两种稳定币都被加密资产超额抵押,并且都依靠价格预言机来维持与美元挂钩。与USDT和USDC等中心化代币不同,它们可以无需许可地被铸造(DAI),值得注意的是,可以将USDC等经过许可的中心化资产用作抵押品。此外,这些稳定币的超额抵押性质意味着它们非常资本密集,并且加密资产的高度动荡,高度相关的性质使这些稳定币在过去容易受到加密震荡的冲击。
所有这些使我们进入了算法稳定币。算法稳定币是一种确定性地(即使用算法)调整其供应量的代币,以使代币的价格朝价格目标(2)的方向移动。在最基本的水平上,算法稳定币在高于目标价格时会扩大其供应,而在低于目标价格时则会收缩。
与其他两种类型的稳定币不同,算法稳定币既不能以美元一对一地赎回,也没有目前由加密资产抵押支持(3)。最后,也许也是最重要的一点是,算法稳定币通常具有很高的反身性(reflexive):需求在很大程度上是由市场情绪和动力驱动的,这一点受到很多争论。这些需求方的力量被转移到代币供应中,进而在最终成为暴力反馈回路的方向上产生进一步的方向动量。
每种稳定币模型都有其权衡。很少关注中心化的投资者将不会对USDT和USDC有任何问题。其他人会发现,资本效率低下的过度抵押是值得付出的代价,以获得一种坚定锚定的无需许可且去中心化的货币。但是,对于那些对这两个选项都不满意的人,算法稳定币是一个诱人的选择。
2
算法稳定性的反身性与悖论
为了使算法稳定币长期可行,它们必须实现稳定性。对于许多算法稳定币而言,由于其固有的反身性,因此特别难以实现此任务。算法上的供应变化旨在是反周期的;扩大供应量应降低价格,反之亦然。然而,实际上,供应变化通常会自发地放大方向动量(4),特别是对于不遵循“铸币税股份”模型的算法模型,即通过将稳定币代币与价值产生代币和债务融资代币分离开来。
对于非算法稳定币,网络引导不涉及博弈论的协调。每个稳定币(至少在理论上来说)可兑换等值的美元或其他形式的抵押品(5)。相比之下,算法稳定币的成功价格稳定性完全无法保证,因为它完全由集体市场心理决定。Haseeb Qureshi恰当地指出了这一点:“这些计划利用了一个关键见解:稳定币最终是一个Schelling点。如果足够多的人相信该系统能够生存,那么这种信念就会导致确保其生存的良性循环。”
的确,如果我们更加仔细地考虑算法稳定币要实现长期稳定将需要什么,我们会发现一个明显的悖论。为了实现价格稳定,算法稳定币必须扩展到足够大的市值,以使买卖订单不会引起价格波动。但是,纯算法稳定币增长到足够大的网络规模的唯一方法是通过投机和反身性,而高反身性增长的问题在于它是不可持续的,并且收缩通常也是反身性的。因此,自相矛盾:稳定币的网络价值越大,它对大价格冲击的适应力就越大。然而,只有高度反身的算法稳定币(易于出现极端的扩张/收缩周期的那些币)才有可能首先达到大型网络估值。
反身性也有类似的悖论。为了使它对越来越多的人和组织可行,它必须越来越具有流动性,稳定性和接受性。多年来,比特币的这些特征不断增长,使其被最初的暗网参与者,后来的富裕技术人员以及最近的传统金融机构所接受。在这一点上,比特币已经在反身周期的深度中获得了抵抗力,这是算法稳定币也需要遵循的路径。
3
Ampleforth:一个简单但有缺陷的算法稳定币
现在让我们从抽象理论转向算法稳定币的现实世界,首先从当今存在的最大但最简单的协议开始:Ampleforth。
如前所述,Ampleforth(AMPL)与Ferdinando Ametrano提出的《Hayek Money》概念几乎相同。AMPL的供应根据每个AMPL的每日时间加权平均价格(TWAP)根据确定性规则进行扩展和收缩:低于价格目标范围(即,低于0.96美元),供应收缩;高于价格目标范围(即,高于1.06美元) ,供应增加。至关重要的是,每个钱包都按比例“参与”了每次供应变化。如果在rebase之前爱丽丝持有1,000个AMPL,而供应量增加了10%,那么爱丽丝现在将持有1,100;如果Bob拥有1个AMPL,那么他现在拥有1.1个AMPL。
网络范围内的“rebase”是将Ampleforth的算法模型与其他协议采用的铸币税份额模型的区分之处。尽管Ampleforth白皮书没有提供与多代币方法相对的单代币rebasing的基本原理,但该设计决策似乎有两个主要依据。
首先是简单性。无论它在实践中如何运作,Ampleforth的单代币模型都具有其他算法稳定币无法比拟的优雅简洁性。其次,Ampleforth的单代币设计声称是最公平的算法稳定币模型。与法定货币政策行动形成鲜明对比的是,法定货币政策行动使那些“最接近”货币来源的个人受益最大(“坎蒂隆效应”),Ampleforth的设计使所有代币持有人在每次重新设定基调后都能保持相同的网络份额。阿美特拉诺(Ametrano)在2014年的论文中指出了这一点,他详细介绍了货币政策行动的“严重不公平”,并将其与《Hayek Money》的相对公平性进行了对比。
这就是Ampleforth模型的推定理由,该模型已被其他rebasing代币(如BASED和YAM)复制。但是,在探讨该模型的缺陷之前,我们可能首先要查看可供我们使用的有关Ampleforth表现的一年半数据。自从2019年中期开始(仅超过500天)以来,Ampleforth的每日资产调整中有四分之三是正数或负数,换句话说,自启动以来,AMPL的TWAP已超出目标范围的75%以上。可以肯定的是,该协议仍处于起步阶段,因此仅凭这些理由将其否定还为时过早。尽管如此,我们很快将研究经过修改的“铸币税”稳定币Empty Set Dollar,在其诞生的头几个月中,如何保持比Ampleforth稳定两倍以上的稳定性。

Ampleforth的捍卫者经常摆脱缺乏稳定性的想法;他们中的许多人甚至会讨厌“算法稳定币”的标签。他们的论点是,使Ampleforth成为投资组合多元化的“不相关的储备资产”就足够了。但是,这种说法值得怀疑。例如,根据随机数生成器每天rebase的一种加密货币。像Ampleforth一样,该代币将具有“明显的波动足迹”,但仅凭这个原因,它肯定不会有价值。Ampleforth的价值主张取决于其趋于均衡的趋势,这一品质理论上可使AMPL成为价格标价的货币。
但是会吗?想象一下,如果Ampleforth摆脱了至今的“粘性”性质,并将价格波动完全转移到了供应波动中,从而每个AMPL的价格将基本保持稳定。这个“成熟的” Ampleforth是否真的是交易基础货币的理想选择?
在这里,我们讨论了问题的症结所在以及Ampleforth设计的中心缺陷。即使AMPL的价格达到1美元,个人持有的AMPL的购买力也会在达到1美元的过程中发生变化。早在2014年,罗伯特·萨姆斯(Robert Sams)就Ametrano的《Hayek Money》阐明了这一确切问题:
价格稳定不仅关系到稳定计价单位,还关系到稳定货币的价值存储。《Hayek Money》旨在解决前者,而不是后者。它只是将固定的钱包余额与波动的代币价格进行交易,将固定的代币价格与波动的钱包余额进行交易。最终结果是,《Hayek Money》钱包的购买力与比特币钱包余额一样不稳定。
最终,Ampleforth的简单性(其简单的单代币rebasing模型)是一个错误,而不是功能。AMPL代币是一种投机工具,当需求高时会奖励持有人通货膨胀,而当需求低时则迫使持有人成为债务融资人。因此,很难看到AMPL如何既可以达到这一投机目的,又可以实现稳定性,这是稳定币的必要先决条件。
4
多代币“铸币税”替代选择
罗伯特·萨姆斯(Robert Sams)的《铸币税股份》愿景从未成为现实,但是最近出现了一种新型的算法稳定币项目,该项目具有许多核心要素。
仅仅诞生一周多的时间,Basis Cash是对复兴Basis的公开尝试,Basis Cash是一个算法稳定币项目,在2018年筹集了超过1亿美元的资金,尽管倍受赞誉,但从未最终启动。与Basis一样,Basis Cash是一个多代币协议,由三个代币组成:BAC(算法稳定币),Basis Cash Shares(网络扩展时其持有人可以要求BAC通胀)和Basis Cash Bonds(可以购买)当网络处于收缩状态时可以打折,并且可以在网络退出通缩阶段时兑换为BAC。Basis Cash仍处于开发的早期阶段,并且遇到了一些早期开发障碍。该协议尚未进行成功的供应变更。
但是,自9月份以来,又有另一个铸币税股份式协议“Empty Set Dollar(ESD)”生效,并且已经经历了多个供应扩展和收缩周期。实际上,到目前为止,ESD已经历达到200多次供应“时期”(每八小时一次),其中60%发生在当ESD的TWAP在$ 0.95 
乍一看,ESD的机制设计似乎是Basis和Ampleforth的混合体。像Basis(和Basis Cash)一样,ESD利用债券(“优惠券”)来资助协议债务,债务必须通过销毁ESD来购买(因此通过合约供应),并且可以在协议扩展后赎回为ESD。但是,与Basis不同,ESD没有第三个代币,该代币在网络在还清债务后(即在赎回票息后)扩展时要求通货膨胀奖励。代替这第三个代币,ESD持有者可以在ESD DAO中“绑定”(即参股)其ESD,以按比例分配每次代币扩张的份额,类似于Ampleforth的rebase。
至关重要的是,与DAO解除绑定的ESD需要一个“暂存”期,其中ESD代币被临时“暂存” 15个周期(5天),既不能由其所有者交易也不能获得通货膨胀奖励。因此,ESD的分阶段模型的功能类似于Basis Cash Shares,因为将ESD绑定到DAO并购买Basis Cash Shares都预先假设了风险(ESD的流动性风险;BAS的价格风险)具有未来的通货膨胀奖励的潜力。确实,尽管ESD使用两代币模型(ESD和优惠券)代替了Basis Cash的三代币模型,但ESD暂存期的最终结果是ESD变成了事实上的三代币系统,并以绑定的ESD作为模拟Basis Cash Shares。
5
对比单代币和多代币算法稳定币模型
显然,与Ampleforth的单代币rebase模型相比,多代币rebase设计包含了更多变化的部分。然而,这种增加的复杂性对于为其提供的潜在稳定性来说是一个很小的代价。
简而言之,ESD和Basis Cash采用的设计的结果是,包含了系统固有的反身性,而系统的“稳定币”部分则(在某种程度上)与市场动态隔离(10)。具有风险偏好的投机者可以在供应收缩期间引导协议,以换取将来从扩展中受益。但是,仅在理论上,仅希望拥有具有稳定购买力的稳定币的用户就可以持有BAC或ESD,而无需购买债券,息票,股票或将其代币绑定到DAO。这种无rebasing的性质具有与其他DeFi原语可组合性的额外好处。与AMPL不同,BAC和(无绑定)ESD可以用作抵押或借出,而不必考虑网络范围内持续不断的供应变化的复杂动态。
Ampleforth创始人兼首席执行官Evan Kuo批评像Basis Cash这样的算法稳定币项目,因为它们“依靠债务市场(即债券)来调节供应。Kuo劝告人们不要使用这些“僵尸思想”,因为这些算法稳定币是有缺陷的,因为像传统市场一样,它们“将始终依靠最后的放款人(即纾困)”。
但是,Kuo的论点是有疑问的,因为它假设的条件是缺乏任何理论依据,依赖债务市场(“纾困”)本质上是危险的。实际上,由于道德风险,债务融资在传统市场中是有问题的。“太大而不能倒闭”的企业实体可以通过将纾困成本社会化来承担未受到惩罚的风险。像ESD和Basis Cash这样的算法稳定币不具有房利美和房地美在2008年金融危机期间享有的奢侈支持。对于这些协议,系统之外没有最后的贷款人可以将救助成本转移到该贷方。ESD或Basis Cash完全有可能陷入债务螺旋式增长,在这种螺旋式中,债务堆积而没有金融家的意愿,协议就崩溃了。
实际上,Ampleforth还要求债务融资,以避免死亡螺旋上升。所不同的是,这种债务融资隐藏在大众目光之下,因为它分布在所有网络参与者中。与ESD和Basis Cash不同,如果不同时充当协议的投资者,就无法加入Ampleforth系统。在网络处于收缩状态时持有AMPL类似于承担该网络的债务(使用Maple Leaf Capital的措辞为“充当中央银行”),因为AMPL持有者会在每次负供应基础上损失代币。
从第一性原理推论和经验数据来看,我们可以得出结论,与“单代币rebasing”替代方案相比,这种多代币且受“铸币税股份”启发的模型具有明显更高的内置稳定性。的确,费迪南多·阿梅特拉诺(Ferdinando Ametrano)最近从2014年开始更新了他对《Hayek Money》的“第一个简单化实现”,鉴于上述问题,他现在赞成基于多代币,基于铸币税的模型。
然而,即使多代币算法稳定币优于其单代币同行,也无法保证这些算法稳定币中的任何一种都能长期持续发展。确实,算法稳定币的底层机制设计排除了任何此类保证,因为如上所述,算法稳定币的稳定性最终是基于博弈论协调的反身性现象。即使对于像ESD和Basis Cash这样的协议,它们将交易,稳定购买力代币与价值应计和债务融资代币分离开来,只要有投资者愿意,稳定代币就将保持稳定。在需求下降时引导网络。当不再有足够的投机者认为网络具有弹性时,网络将不再具有弹性。
6
部分储备稳定币:算法稳定币的新时代?
纯算法稳定币所具有的投机性是不可避免的。但是,最近出现了一些雏形协议,试图通过利用部分资产抵押(“部分储备”)来控制算法稳定币的反身性。
这里的见解很简单。Haseeb Qureshi在他的观察中是正确的,“从根本上讲,您可以说支持铸币税股份的"抵押"是系统未来增长中的股份。” 那么为什么不以实际抵押品补充这种投机性“抵押品”,以使系统更强大呢?
ESD v2和Frax正是这样做的。ESD v2仍处于研究和讨论阶段,此后最终将由治理部门投票表决。如果实施,这个升级将对当前的ESD协议进行几项实质性更改。其中最主要的是引入“储备金要求”。
在新系统下,ESD协议的目标是20%至30%的储备金率,最初以USDC计价。这些储备的部分资金来自协议本身,该协议会在ESD高于某个目标价格时在公开市场上出售ESD,并且也希望由想要与DAO解除绑定的ESD持有者(他们必须向储备金进行存款)。然后,通过自动购买ESD直到达到最低储备要求,这些USDC储备可用于在收缩期间稳定协议。
尚未推出的Frax是创建部分抵押算法稳定币的更为优雅的尝试。与基础现金一样,Frax包含三个代币:FRAX(稳定币),Frax股票(管理和价值应计代币)和Frax债券(债务融资代币)。但是,与到目前为止讨论的所有其他算法稳定币不同,FRAX可以始终以1美元的价格铸造和赎回,这意味着套利者将在稳定代币价格方面发挥积极作用。
这种铸造/兑换机制是Frax网络的核心,因为它利用了动态的分数储备系统。要铸造一个FRAX,用户必须存入一定数量的Frax股票(FXS)和其他价值一美元的抵押品(USDC或USDT)组合。FXS与其他抵押品的比例由对FRAX的需求动态确定(随着需求的增加,FXS与其他抵押品的比例会增加)。锁定FXS来铸造FRAX将对FXS供应产生通缩效应,因此,随着需要更多FXS铸造FRAX,对FXS的需求自然会随着供应下降而增加。相反,正如Frax的文档所指出的,在收缩期间,“该协议对系统进行了抵押,以使FRAX的赎回者从系统中获得更多的FXS和更少的抵押品。这增加了系统中抵押品占FRAX供应比例的比例,随着FRAX的支持增加,市场对FRAX的信心也增强了。”
有效地,动态抵押充当稳定的反周期机制,使Frax协议可以在需要时钝化极度反身性的有害影响。但是,如果市场选择的话,它还允许该协议在将来变得完全无抵押成为可能。从这个意义上讲,Frax的动态抵押机制是“不可知论的”。
Frax和ESD v2均未启用,因此在实践中能否成功还有待观察。但是至少从理论上讲,这些混合的,部分储备的协议是将反身性与稳定性结合起来的有前途的尝试,同时仍然比DAI和sUSD等过度抵押的替代方案具有更高的资本效率。
结论思想
算法稳定币是一种具有吸引力的是货币实验。尽管查理·芒格(Charlie Munger)的格言始终如一:“告诉我动机,我告诉你结果”,但这些协议具有博弈论上的复杂性,仅凭先验推理就很难完全把握住。此外,如果过去的加密货币市场周期可以作为指引,我们应该为这些动态做好准备,以掩盖理性预期的方式发挥作用。
然而,在此早期阶段关闭算法稳定币将是愚蠢的。忘记赌注到底有多高也是错误的。哈耶克(Hayek)在1976年的《货币贬值》中写道:“我相信我们可以做得比黄金更好。政府不能做得更好。自由企业,即毫无疑问会从竞争过程中产生的提供优质资金的机构。”尽管算法稳定币仍处于混乱状态,但它们最终可能成为哈耶克关于蓬勃发展的货币市场的愿景的蓝图,并为之奠定基础。
披露:作者可能持有本文提到的代币。
















