
作者:阿剑
文章题目来自 Bitcoiner 熊越。
比特币的 Taproot 软分叉升级将于比特币区块高度 709632 处(预计是 2021 年 11 月 15 日)激活。此次升级包含了许多重要而精彩的内容,然而,在中文世界里却缺乏足够的重视。本文将从技术角度简要介绍 Taproot 的升级内容,并以此体现比特币的发展方向。
常见的说法是,Taproot 提升了比特币的隐私性、智能合约功能性、同质性,云云。但是,要想理解 Taproot 升级的内容和想象空间,我们得先了解一些比特币。
比特币上的智能合约
许多人不了解的是,比特币也支持编程智能合约 2,只不过其智能合约的类型与其他区块链(比如以太坊)的不同。详细解释这种区别需要专门的一篇文章,这种区别在这篇文章里也不重要。这里仅仅介绍比特币智能合约编程的几个常见的模块 3,方便大家理解其应用场景:
多签名合约。比特币支持多签名授权使用资金:在 N 个记录好的公钥中,必须有 M 个公钥所对应的私钥(对同一个操作的)签名,该笔资金才可动用。比特币支持最多 15 个公钥的多签名合约。
时间锁。用户可以使用两种类型的时间锁来规定一笔资金的可用时段:(1)CLTV,绝对时间锁,以具体的时间或具体的区块高度来定义,过了这个时间才可动用;(2)CSV,相对时间锁,比如生成该项资金的交易上链的 1000 个区块后,该笔资金才可动用。
多条件编程。即在脚本中使用 “IF ... ELSE ...” 式的语句,为同一笔资金设定多个解锁条件,任一条件满足即可使用该资金。比如:“A 公钥所对应的私钥可解锁,或者,在区块高度 XXXX 以后,B 公钥所对应的私钥可以解锁,或者,在该交易上链的 YYYY 个区块以后,A、B、C 三个公钥中任意两个所对应的私钥可以解锁”
如读者可以想象的,这几个模块看起来非常简单,组合起来可能性却非常多:多签名合约定义了不同主体的权限,可以适应极为丰富的应用场景,从公司运营,到家庭金库;时间锁则规定了不同主体在不同时段的权限。而多条件则显著放大了这些权限控制的组合效果。
你甚至仅凭几个条件,就可以做出一个支持社交恢复、带遗产分配效果的合约:“我(A 公钥)可以控制这笔资金;如三个月无人动用,我(B 公钥)和四个朋友,五取其三可以一起控制这笔资金;如果一年无人动用,我的妻子可以控制这笔资金”。
但是,这些合约要实际上派上用场,两个因素就不能忽视:效率性和隐私性。
效率性的意思是,比特币交易的手续费是根据交易的体积来计算的,更多条件的脚本会占用更大的空间(以字节数计),交易费也会更高。
隐私性的考量是,脚本曝光会使其他人知道某些公钥之间是有身份关联的,更容易分析出公钥主人的真实身份。
在当前,比特币的合约体现为 P2SH “地址”(实际上就是一条哈希值)。其特点是,在生成合约时,脚本可以不公开,有需要的直接给脚本的哈希值支付;但是,这些资金在花费时,与这个哈希值对应的脚本就要完全公开出来放到交易中(否则无以验证这个脚本的哈希值正是这个哈希值)。以多签名合约为例,其他人可以直接给这个多签名合约脚本的哈希值支付,但是,当多签名合约的参与者要使用这些资金时,就必须把整个脚本公开 3。
此外,在 SegWit 升级以前,单签名的个人钱包与合约钱包是泾渭分明的,前者是 P2PKH 地址,后者是 P2SH 地址,仅从地址上就可以看出来,这又是一个对隐私不利的因素。在 SegWit 升级之后,支持隔离见证的个人钱包也可采取 P2SH 的形式,但原生隔离见证地址(P2WPKH)和合约地址(P2WSH)仍然是泾渭分明的 4。
了解了这些以后,让我们来看看 Taproot 升级的三大部分(MAST、Schnorr 签名、Taproot)如何做得更好。
默克尔抽象语法树(MAST)
默克尔化抽象语法树(Merklized Abstract Syntax Trees, MAST)5 的含义是,在比特币的脚本验证中支持验证默克尔证据。
默克尔树是将多个数据元素哈希成一个哈希值的密码学方法。其结构和哈希函数的特点决定了,可以提供一些证据(哈希值)来证明,某个数据元素参与生成了这个哈希值。如下图所示:我们将(相邻的)数据元素两两不断哈希,最终生成一个默克尔根。
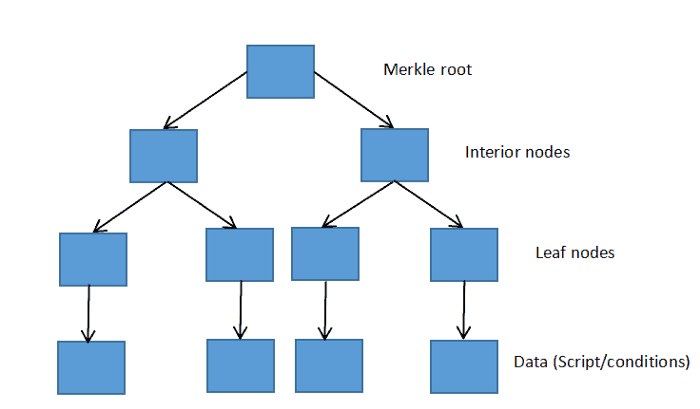
3
同理,如下图,当我要证明红色数据 “Banana” 参与生成了紫色的哈希值(默克尔根)时,我只需提供红色数据和三个绿色的哈希值就可以了,无需曝光实际上共同生成了默克尔根的其余 7 个元素。这就是默克尔树和默克尔证据的作用。
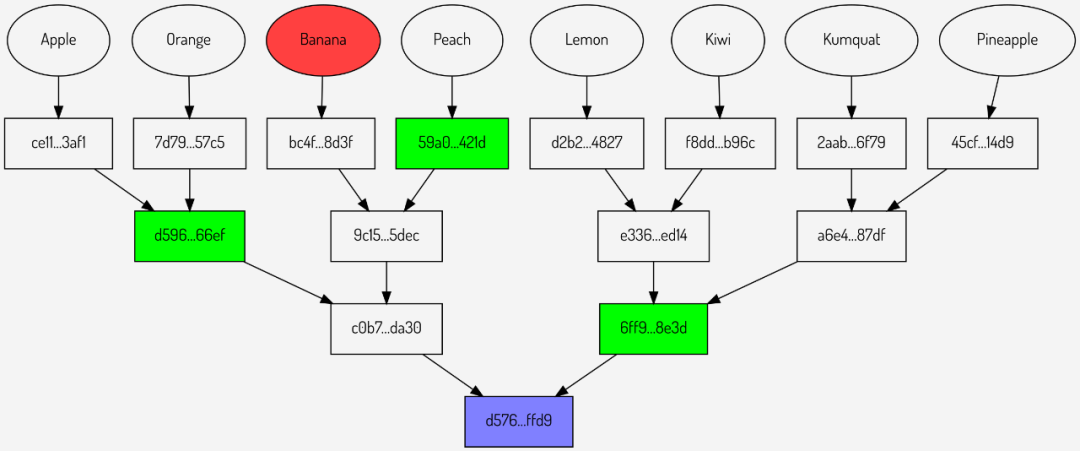
Individual Merkle proofs for Banana, Peach and Kumquat
聪明的读者一定想到了,有了这个功能,合约的编写者就可以把多个条件划为不同的数据元素,哈希出一个默克尔根值来;在需要以某个条件来解锁比特币时,只需证明这个条件在这棵默克尔树上即可,无需公开所有其他条件。
没错,这正是 MAST 的妙用。如下图所示,这笔资金的解锁条件有两个,而编写者把它们分割了开来,用默克尔树抽象成了一个哈希值,在以任一个条件解锁使用时,都不需要公开另一个。
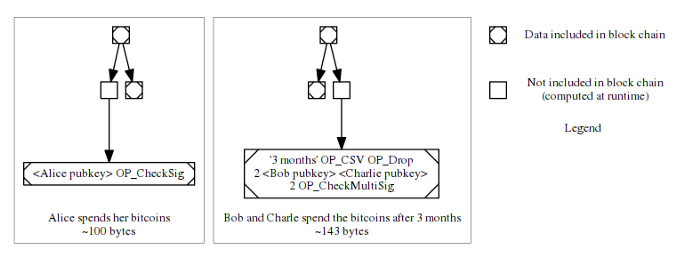
005.png
MAST 在 P2SH 的基础上迈出了一大步,其提升效果首先体现在隐私性上:原本在 P2SH 中,合约在使用时就一定要公开全部的脚本内容,不论那些内容用到没用到,都必须公开;现在,有了 MAST,用户就只需要公开需要用到的解锁条件,无需公开全部内容了;同时,别人也根本不知道你还有多少个条件。
其次,它还在效率上有所提升:用户只需提供需要用到的部分脚本,及其默克尔证据,在整个脚本比较庞大时,这种体积节约的效果会非常明显。
由此,未来的比特币用户可以编写条件非常多的合约,获得更好的控制效果而只需支付更少的手续费;甚至,可以有意包含一些垃圾条件来充实默克尔树,获得隐私提升的效果。
这也是本篇副标题 “哈希即银行” 的由来:比特币的脚本实际上全部围绕着资金的控制,实现这种控制的关键一环正是多条件,而有了 MAST,即使是极多条件的资产管理脚本,也可以压缩成一个哈希值,在使用时仅需暴露一部分。成本的降低可以打开非常多的可能性,等待钱包开发者去一探究竟。
Schnorr 签名
Taproot 升级之后,比特币将不仅支持基于椭圆曲线的密码学签名,还支持 Schnorr 数字签名方案 6。
Schnorr 签名的构造方法在此不提,我们仅介绍其重要属性:签名/密钥 聚合 —— 多个私钥的签名,可以聚合成一个签名,看起来仿佛是一把私钥签出的。签名时,仍然是各私钥持有者各自签名的;验签时,却仿佛这些签名是一把对应于已知公钥(当然就是这些参与者的公钥聚合而成的公钥)的私钥签出的。
也就是说,有了 Schnorr 签名,其他人就无法分辨一个签名到底是单人签出的,还是多人共同签出的了;多签名的解锁条件,可以用一个聚合公钥来替代。所有 n-n 的多签名合约,都可以享受到 Schnorr 签名提供的隐私保护。其最显然的应用就是闪电网络通道,因为闪电网络通道是一个 2-2 的多签名合约;此后,其他人就无法凭借签名的数量来分辨支付通道和个人用户了。
至于 m-n 的多签名合约,也不用担心,别忘了我们有 MAST:我们可以把所有可能解锁的情形都化成一个分支,在使用某个分支时,所提供的签名也只需是聚合签名。例如,假设我们要做一个 2-3 的多签名合约,在公钥 A、B、C 中三取其二,这个多签名合约效果等同于 “要么(A、B)解锁、要么(B、C)解锁、要么(A、C)解锁”,这可以理解为一个多条件的脚本,每个条件都是一个 2-2 多签名,因此也都可以用相应的聚合公钥来定义解锁条件(而无需以多签名来定义)。所以,当我们需要以某种组合解锁资金时,只需用 MAST 暴露一个分支、提供一个签名,他人依然不知道这到底是一个人,还是两个人,还是多个人。
还没完呢。
Taproot
按我们这种理解的路径,Taproot 升级的最后一个部分就是 Taproot,是其名字的由来。在提出这个概念时,Gregory Maxwell 写道 7:
在讨论默克尔化脚本时,一个大家常常提起的问题是,我们能否实现一种精巧的合约,使其与最常见、最无聊的支付没有分别。不然的话,使用这些时髦技术的输出的匿名集,也就是另一个小众集合而已,在实践中没有多大的意义。
在这里,Maxwell 敏锐地抓住了问题的要点:比特币的隐私保障来自于 “大隐隐于市”,最好所有的资金单元(UTXO)看起来都一个样,这样用户的真实身份、真实构成才最难把握。但是,在引入新的功能时,总免不了要提出新的 “地址” 类型,如果使用这种功能的用户很少,则每一个用户暴露真实身份的可能性都会大大增加,而这一点可能导致这些新功能根本不会被使用,从而失去意义。
而且,尽管 MAST 在合约的隐私性上有重大作用,但如果还像过去那样,个人钱包是个人钱包,合约钱包是合约钱包,一目了然的话,就不能不说,这样的隐私性仍然是有瑕疵的。
人们亟需一种办法,来终结这种 个人钱包/合约钱包 的区分,为比特币的隐私性补上点睛之笔。为此,最起码要实现的一点是,这种带有合约的钱包,在用户个人日常使用中,其代价与普通的个人钱包没有区别(经济性)。
Taproot 就是这样的一种办法,它利用了密钥聚合的特点,提出了自带两种使用路径的脚本模式:一种是 n-n 的多签名合约;另一种是用户自定义的合约脚本。
沿用 Maxwell 原文中的例子:
假设两个用户各有公钥 A、B,两人聚合公钥 A + B = C,再生成最终公钥 P = C + H(C||S)*G,其中 S 为自定义的脚本。就以这个最终公钥 P 来定义资金的解锁条件。
假设两个用户都在线,他们很容易可以共同使用这笔资金,只要其中一方在签名时在自己的私钥里加上 H(C||S) 即可;
如果只有其中一方在线,比如 S 定义了 B 可以花费资金的条件,Taproot 的规则使得公钥 B 用户可通过揭示聚合公钥 P 以及 H(C||S) 并提供可以满足 S 的条件来使用资金。
这里用的是 2-2 多签名合约,但用户可以想到,只要密钥聚合的技术可用,1-1 也就是单签名同样可以利用这种编写脚本的办法。重要的是:(1)尽管这是一个带有自定义合约的资金,但在不动用合约、仅使用 n-n 多签名时,其手续费成本与单签名解锁的资金没有区别!(2)在 n-n 多签名使用时,他人完全不知道这笔资金还可以用其他方式来解锁使用!
这样一来,个人用户和合约用户都可以统一在一种脚本模式(P2TR “地址”)下,个人用户放心给自己的资金加上合约,无需担心日常会付出更高的手续费代价;合约用户与个人用户因为使用同一种 “地址” 而享受到更大的匿名集,甚至于在大部分情况下都无需暴露自己使用了合约。皆大欢喜。
总而言之,在 Taproot 之后,他人将无法从地址形式上分辨一个 P2TR 地址到底是个人用户还是合约用户;由于 Schnorr 签名的效果,当这个地址里的资金使用单签名来解锁时,他人将无法分辨这到底是一个人在使用,还是 n 个人一起使用,也无法知道这个地址是否还有自定义的脚本;由于 MAST 的效果,当用户使用自定义的脚本来花费资金时,只需暴露需要用到的部分脚本;他人虽然知道了这个地址有自定义的脚本,但整个脚本到底包括哪些条件,仍然是不可知的。
因此,尽管有人质疑 Taproot 可能反过来给比特币的隐私性带来损害 7,但我完全不这么担心。因为 Taproot “地址” 在便利性、隐私性、经济性上,都已毫无疑问是比特币史上最佳,它完全有希望可以统一比特币的 “地址” 类型,形成比特币有史以来最大的匿名集。
结语
对于了解一些密码学技术的人来说,学习比特币的开发和升级是很愉快,乃至令人眼界大开的事。在其升级中,你可以看到人们孜孜不倦地使用密码学来不断优化这个系统 —— 得益于这个系统本身的模块化特性,这些优化都真实可感。Taproot 正是其中的代表。
我相信,学习比特币(尤其是 Taproot)的过程会告诉读者,什么才是真正的 “密码学货币”。
Taproot 可能是比特币历史上最重要的一次升级,将造就有史以来最纯粹的密码学货币 —— 将密码学利用到极致、最轻量、生命力最顽强的货币。
致谢
感谢 @hou123,@曾汨 对本文的富有教益的反馈。
脚注:
比特币升级提案 Taproot 技术解读,https://www.btcstudy.org/2021/09/29/bitcoin-taproot-a-technical-explanation/
Bitcoin Wiki·智能合约,https://en.wikipedia.org/wiki/Smart_contract
精通比特币中译本·第七章:高级交易和脚本,https://github.com/tianmingyun/MasterBitcoin2CN/blob/master/ch07.md
Types of Bitcoin transactions - Part II Segwit,https://blog.susanka.eu/types-of-bitcoin-transactions-part-ii-segwit/
什么是比特币默克尔化抽象语法树,https://www.btcstudy.org/2021/09/07/what-is-a-bitcoin-merklized-abstract-syntax-tree-mast/
Schnorr 签名如何提升比特币,https://www.btcstudy.org/2021/09/09/how-schnorr-signatures-may-improve-bitcoin/
Taproot: Privacy preserving switchable scripting,https://lists.linuxfoundation.org/pipermail/bitcoin-dev/2018-January/015614.html
用大白话解释 Taproot 对隐私性的影响,https://www.btcstudy.org/2021/09/23/explain-like-im-not-a-developer-taproot-privacy/
值得阅读的文章 National Affairs: 比特币与美国的财政清算
https://mp.weixin.qq.com/s/VwRE4mBia4AlMx6MZbvZjA
@Bruce:对于美国货币政策的恶性循环的灰犀牛,部分美国政治精英已意识到比特币是走出无锚美元价值涣散的一种选择,为了让民众和企业对美国财政清算最坏可能性进行准备,文章呼吁美国政策制定者全面开放比特币和数字资产的监管,甚至建议财政部考虑用比特币取代其持有的一小部分黄金
All Ye Faithful
https://blog.bitmex.com/all-ye-faithful/
@大麦:100x 小黑哥论「Crypto与宗教」
欺诈证明与虚拟机
https://medium.com/@cpbuckland88/fraud-proofs-and-virtual-machines-2826a3412099
@郭宇:这篇文章比较了 Arbitrum 与 Optimism 利用欺诈证明实现 Rollup 的不同机制。
The Great Online Game
https://www.notboring.co/p/the-great-online-game
@Leon:全人类在网上的活动,已经成为了一场巨大的meta game,它是不是“元宇宙”已经不重要了。

















