Verkle Tree作为ETH2.0升级的一个重要部分,其相比于Merkle Tree,在Proof的大小上,有着很大的提升;对于规模在十亿级别的数据,Merkle Tree的proof大约需要1kB,而对于Verkle Tree, 它将小于150Bytes。
Verkle Tree的概念在2018年推出,具体的可以参考论文Verkle Tree;本文将主要介绍Verkle Tree的原理。
Merkle Tree
Merkle Tree是一种常见的Accumulator,它可以用来证明某个元素存在于Accumulator中,如下图所示:
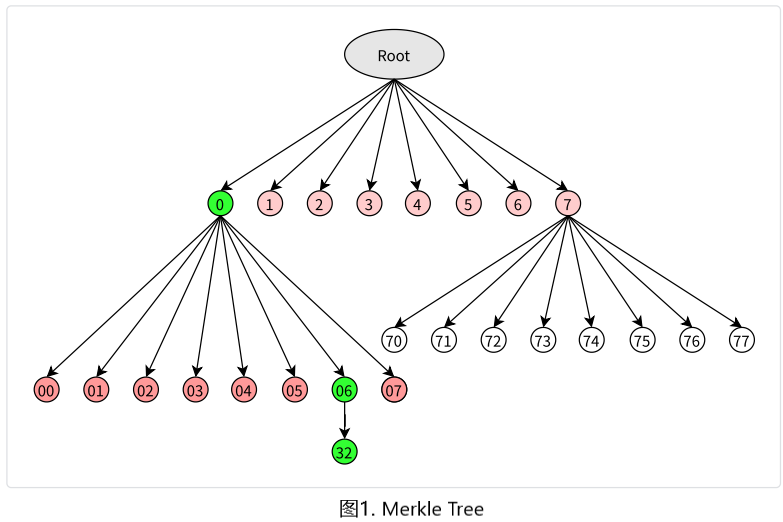
如果想要证明(key: value)= (06: 32)在这个Tree中(绿色标记),那图中所有红色标记的 node都需要包含在Proof中,然后verifier根据图中所示的路径计算出Root,并和期望的Root(灰色标记)进行比较。
可以预见的是,随着Tree的深度和宽度变大,则Proof的大小同样会变大(对于branched-2,复杂度为![]() ,对于branched-k,复杂度为
,对于branched-k,复杂度为![]() ;而且,verifier需要从Tree的底层逐步向上进行大量的Hash计算,一直到顶层,随着Tree的深度和宽度的增加,verifier的工作量也将会变得可观(这是难以接受的)。
;而且,verifier需要从Tree的底层逐步向上进行大量的Hash计算,一直到顶层,随着Tree的深度和宽度的增加,verifier的工作量也将会变得可观(这是难以接受的)。
Verkle Trees - concept
前面章节提到,单纯的增加Tree的宽度,虽然能减小Tree的深度,但不能降低proof的大小,那是因为Proof的大小由最初的变为了 ; 即, 对于每一层, prover都需要提供 k-1 个额外的节点信息, 论文Verkle Tree给出了⼀个方案, 使得proof的复杂度降低到![]() , 如果令 k=1024 , 则Proof将会缩
, 如果令 k=1024 , 则Proof将会缩 ![]() 倍。
倍。
Verkel Tree的设计如下图所示:
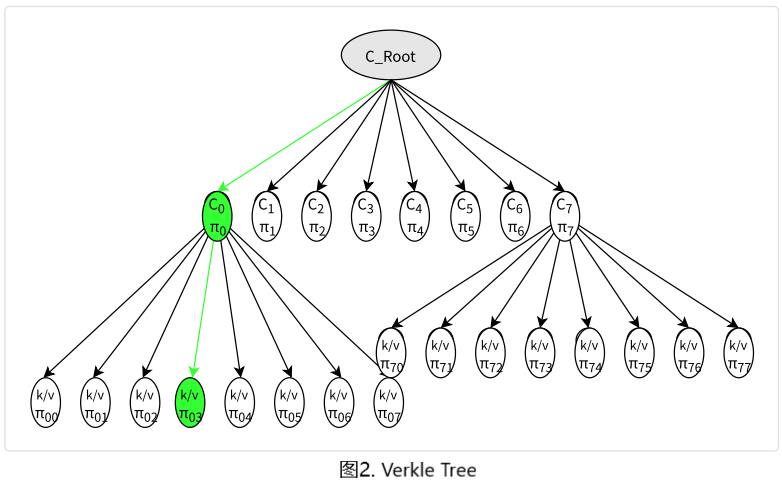
每一个节点都包含了两个信息(1)Value;(2)存在性证明π,比如图中的绿色标记![]() 表示H(k,v)存在于承诺
表示H(k,v)存在于承诺![]() 中,
中,![]() 为这个表述的proof;同理,
为这个表述的proof;同理,![]() 表示
表示![]() 存在于承诺
存在于承诺![]() 中,
中,![]() 为这个表述的证明。
为这个表述的证明。
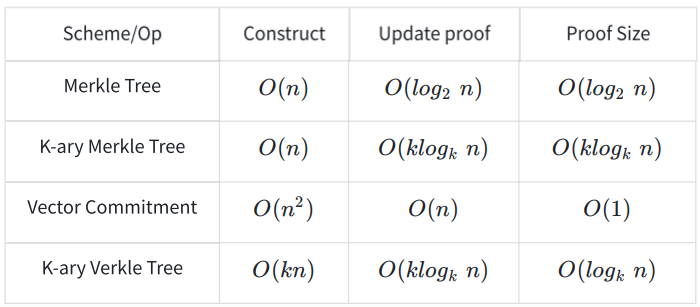
在论文Verkle Tree中,这种存在性证明的方式称为Vector commitment;若直接采用Vector commitment的方案对原始数据进行存在性证明,其可以获得O(1)复杂度的Proof,但是构建Proof的复杂度和更新Proof的复杂度分别为O(n²),O(n)。因此,为了在它们之间保持一个平衡,论文Verkle Tree里采用的K-ary的Verkle Tree的方案(如上图所示),使得构建Proof,,更新Proof,Proof的复杂度分别为O(kn),O(![]() ),O(
),O(![]() ),具体性能对比如表1所示:
),具体性能对比如表1所示:
本文并不打算详细的去介绍vector commitmenr的一些具体方案,有兴趣的可以直接去阅读论文;庆幸的是,我们有比vector commitment更有效的工具 - polynomial commitment(多项式承诺)。给定一组坐标集合![]() 和值集合
和值集合![]() ,你可以构建一个多项式(Lagrange interpolation)满足
,你可以构建一个多项式(Lagrange interpolation)满足![]() ,然后对这个多项式进行承诺。常见的多项式承诺方案有KZG10 和 IPA(此时,承诺就是椭圆曲线上的一个点,大小一般在32-48Bytes之间)。
,然后对这个多项式进行承诺。常见的多项式承诺方案有KZG10 和 IPA(此时,承诺就是椭圆曲线上的一个点,大小一般在32-48Bytes之间)。
Basis
KZG for single point
以KZG10承诺为例,对于多项式P(x),我们用![]() 表示多项式承诺。我们知道,对于多项式P(x),如果(z)=y,则有(x−z)|(P(x)−y),即如果令Q(x)=(P(x)−y)/(x−z),则Q(x)是一个多项式。
表示多项式承诺。我们知道,对于多项式P(x),如果(z)=y,则有(x−z)|(P(x)−y),即如果令Q(x)=(P(x)−y)/(x−z),则Q(x)是一个多项式。
现在,你为多项式P(x)满足P(z)=y 生成一个证明:即,计算![]() ,并且发送给Verifier,Verifier需要验证:
,并且发送给Verifier,Verifier需要验证:
![]()
因为s是有限域F上随机选取的一个点,因此,prover作恶成功的概率为 degree(Q)/P(Schwartz–Zippel lemma)。
KZG for multi-points
现在,你想证明多项式P(x)在![]() 上的值分别为
上的值分别为![]() 。为此,你需要定义两个多项式:
。为此,你需要定义两个多项式:
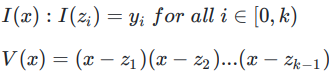
则,根据前面的描述,需满足V(x)|(P(x)−I(x)),即,存在多项式Q(x)满足:
Q(x)∗V(x)=P(x)−I(x)。
因此,Pover需要提供对多项式P(x)和Q(x)的承诺![]() ,并发送给Verifier;Verifier本地计算
,并发送给Verifier;Verifier本地计算![]() ,然后校验等式:
,然后校验等式:
![]()
可以看到,无论Points有多少个,proof的大小是恒定的,如果选择Bls12-381曲线,Proof的大小只有48Bytes,这一点非常高效。
Verkle Tree - ETH
相比于Merkle Tree,为了证明一个元素的存在性,prover仍然需要提供![]() 大小的proof,Verkle Tree在proof大小上实现了巨大的提升。
大小的proof,Verkle Tree在proof大小上实现了巨大的提升。
让我们看一个Verkle Tree的简单示例:
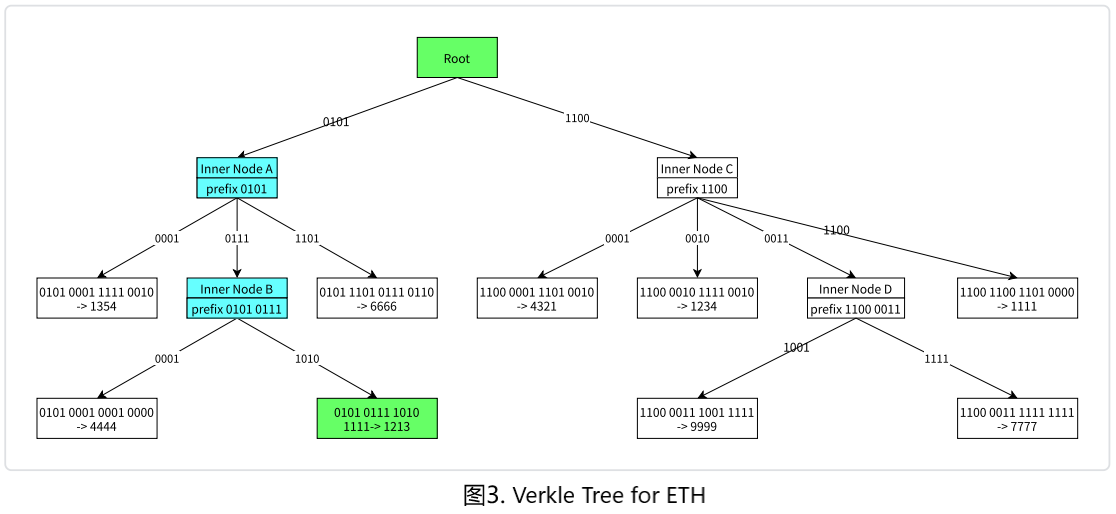
可以看出, 和Merkle Patricia Tree结构类似, node可以分为三类:empty node、inner node和leaf node,每个inner node tree的宽度为16(16进制表示0000->1111);为了证明leaf node的状态为(0101 0111 1010 1111 -> 1213),我们需要对Inner node A和 Inner node B进行承诺:
a. 证明Inner node B的承诺在索引1010处的值为hash(0101 0111 1010 1111, 1213);
b. 证明Inner node A的承诺在索引0111处的值为hash(cm_B);
c. 证明node Root的承诺在索引0101处的值为hash(cm_A);
把上述承诺分别用![]() 表示,且分别对应多项式
表示,且分别对应多项式![]() ,因此,Prover需要证明的是:
,因此,Prover需要证明的是:
a. ![]()
b. ![]()
c. ![]()
Compress for multi-polys
为了简单, 我们将用![]() 来表示索引, 则prover需要证明, 对于多项式集合
来表示索引, 则prover需要证明, 对于多项式集合![]() ,分别在点
,分别在点![]() 处满足:
处满足:
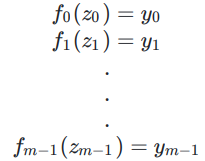
根据前面的描述(KZG for single point),对于每一个多项式,都存在一个商多项式满足:
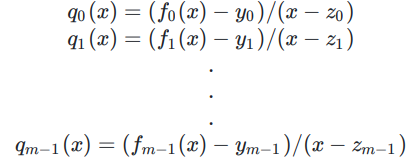
Prover需要对原多项式和商多项式进行承诺,并发送给Verifier:
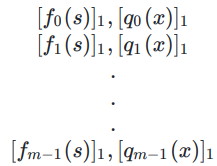
Verifier执行校验:
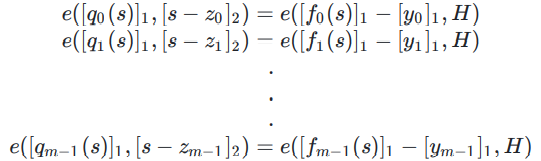
很明显,我们并不想让Verifier执行这么多次的配对操作(这个是昂贵的步骤)。因此,我们需要进行一次Compress,具体如下:
我们随机生成一些随机数![]() ,然后把上述商多项式组合在一起:
,然后把上述商多项式组合在一起:
![]()
我们假设,当且仅当每个![]() 为多项式时,g(x)才是一个多项式(因为随机数的引入,
为多项式时,g(x)才是一个多项式(因为随机数的引入,![]() 之间的分数部分正好抵消的概率很低)。
之间的分数部分正好抵消的概率很低)。
prover对多项式g(x)进行承诺,并发送![]() 给verifier。
给verifier。
接下来,只需要让verifier相信![]() 是对多项式g(x)的承诺:
是对多项式g(x)的承诺:
观察多项式g(x)的形式,其可以写成:
![]()
随机选择一个值t,则有:
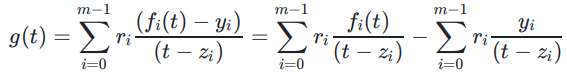
定义多项式:
![]()
其承诺可以用以下方式计算:
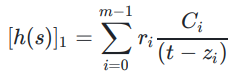
则有:多项式h(x)−g(x)在点t的值为:![]()
令:
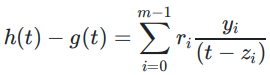
计算商多项式
![]()
计算其承诺![]() ,发送给verifier。
,发送给verifier。
Verifier验证:
a. 计算
![]()
![]()
b. 校验
![]()
Key propertie
a. 该方案允许Prove任意个数的points,且Proof的大小是恒定的(一个承诺,一个proof: π);
b. ![]() 的值可不显式提供,因为它就是下一层值的hash;
的值可不显式提供,因为它就是下一层值的hash;
c. ![]() 的值可不显式提供,可以根据Key判断;
的值可不显式提供,可以根据Key判断;
d. 所用到的公开信息就是被证明的key/value对,和由下而上的没层级对应的承诺。
参考
1. PCS multiproofs using random evaluation - Dankrad Feist; https://dankradfeist.de/ethereum/2021/06/18/pcs-multiproofs.html
2. Verkle trees - vitalik :https://vitalik.ca/general/2021/06/18/verkle.html
3. Verkle Trees paper :https://math.mit.edu/research/highschool/primes/materials/2018/Kuszmaul.pdf
4. Vector commitment:https://eprint.iacr.org/2011/495.pdf
5. Lagrange interpolation:https://en.wikipedia.org/wiki/Lagrange_polynomial
6. KZG10:https://dankradfeist.de/ethereum/2020/06/16/kate-polynomial-commitments.html
7. IPA:https://twitter.com/VitalikButerin/status/1371844878968176647
8. Schwartz–Zippel lemma:https://en.wikipedia.org/wiki/Schwartz%E2%80%93Zippel_lemma
关于我们
Sin7Y成立于2021年,由顶尖的区块链开发者和密码学工程师组成。我们既是项目孵化器也是区块链技术研究团队,探索EVM、Layer2、跨链、隐私计算、自主支付解决方案等最重要和最前沿的技术。
微信公众号:Sin7Y
GitHub:Sin7Y
Twitter:@Sin7Y_Labs
Medium:Sin7Y
Mirror:Sin7Y
HackMD:Sin7Y
HackerNoon:Sin7Y
Email:contact@sin7y.org


















