著者: シアマック・モアレミ、ダン・ロビンソン、パラダイム
編集者: Yangz、Techub News
導入
この記事では、予測市場向けにカスタマイズされた新しい自動マーケット メーカー (AMM)、pm-AMM を紹介します。
AMM とその前身であるマーケット スコアリング ルールは、もともと予測市場に流動性を提供する方法として発明されました。彼らは現在、ほとんどの DEX の取引量を独占しています。しかし皮肉なことに、予測市場では取引量が急激に増加しているにもかかわらず、そのほとんどは AMM ではなくオーダーブックを使用しています。
この考えられる理由の 1 つは、既存の AMM が結果トークンに適していないことです (つまり、イベントが発生した場合のトークンの価格は 1 ドルで、イベントが発生しなかった場合のトークンの価格は 0 ドルです)。結果として生じるトークンのボラティリティは、イベントの現在の確率と予測される市場の期限切れのタイミングに依存します。これは、資産プールによって提供される流動性が一貫していないことを意味します。予測市場が期限切れになると、流動性プロバイダー (LP) は基本的にすべての価値を失います。
この目的を達成するために、私たちはこれらの考慮事項に基づいて最適化された新しい AMM を提案します。これは、AMM 研究における長年の疑問、つまり、特定の種類の資産に対して AMM を最適化することは何を意味するのか、という問題に対処することを目的としています。言い換えれば、特定の資産 (オプション、債券、ステーブルコイン、アウトカム トークンなど) のモデルが与えられた場合、それは適用する AMM にどのような影響を与えるのでしょうか?私たちは、損失とリバランス (LVR) の概念に基づいて、この質問に対する考えられる答えを提案します。
研究結果
私たちは、ガウス スコア ダイナミクスと呼ばれる、いくつかの結果トークンの価格変動のモデルを構築しました。このモデルは、基本的なランダム傾向 (バスケットボールの試合の得点差、選挙の得票差、資産の価格など) が特定の値を超えるかどうかを予測できるため、予測市場に適している可能性があります。将来の特定の有効期限。
このモデルを使用して、これらのトークンに対する新しい不変式ベースの AMM、静的な pm-AMM 不変式を導出します。
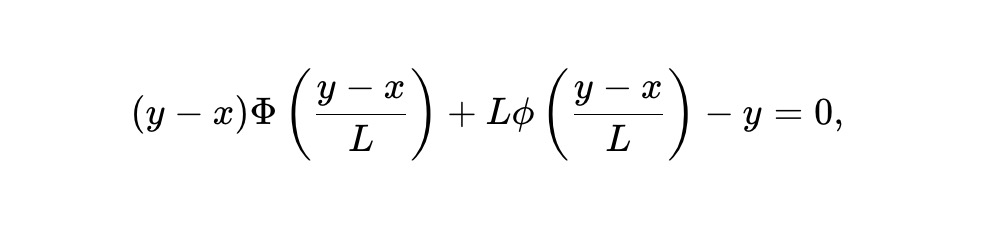
このうち、x は AMM のアウトカム トークンのリザーブ、y はその反対および相補的なアウトカム トークンのリザーブ、L は全体の流動性または比例係数、ϕ と Φ は正規分布の確率密度関数と累積分布関数を表します。それぞれ配布します。
上記の不変条件は、損失とリバランス (LVR) という強力な概念に基づいており、LVR は裁定取引による AMM の損失率が AMM の形状と価格変動に依存すると考えることができます。 AMM で取引される原資産。
資産に対する統一 AMM を定義します。その資産に使用される場合、AMM の LVR は、現在の価格に関係なく、特定の時点でのポートフォリオの価値に比例します。 Milionisらは、価格が幾何学的なブラウン運動(GBM、株式や暗号通貨などの一般的な資産の価格変動の一般的なモデル)に従う資産の場合、UniswapやBalancerなどの一定の幾何平均マーケットメーカーが唯一の統合AMMであると主張しています。一方、静的 pm-AMM は、結果として得られるトークンの提案されたガウス分数動的モデルに従う資産動作用の統合 AMM です。
静的 pm-AMM はすべての価格で均一の LVR (ポートフォリオ値の一部として) を持ちますが、予測市場の有効期限が近づくにつれて LVR は増加します。これは、予測市場は期限が近づくと非常に不安定になる可能性があるためです。 AMM の予想 LVR が有効期限までの残り時間内で常に一定に保たれるように、pm-AMM を調整して流動性を下げるために、有効期限 Tt に依存する動的 pm-AMM 不変量を導出します。
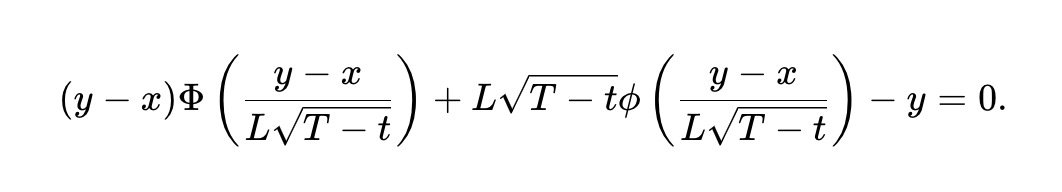
動的な pm-AMM のメカニズムは、流動性を低下させることで、有効期限が近づくにつれて LVR が増加するのを防ぎます。実際のプールでは、特に非裁定取引活動 (したがって手数料) も時間の経過とともに増加する可能性があるため、これは必ずしも望ましいことではありません。ただし、pm-AMM は、流動性プロバイダーが予想される手数料と裁定リスクの配分方法に基づいて流動性を調整するためのフレームワークを提供します。
これらの AMM は、オンチェーン予測市場における受動的な流動性を導くのに役立つ可能性があります。統合 AMM と関連手法の概念は、DEX 設計者にもより広く適用できる可能性があります。DEX 設計者は、これらの手法を使用して、ステーブルコイン、債券、オプション、通貨など、価格変動が幾何学的なブラウン運動に従わない他の種類の資産の AMM をカスタマイズできます。他の派生製品も。
図 1 は、静的および動的 pm-AMM の不変曲線を示し、他のよく知られている不変曲線、すなわち Constant Product Market Maker (CPMM) および Logarithmic Market Scoring Rule (LMSR) と比較しています。動的な pm-AMM の準備曲線は、時間の経過とともに流動性が低下することに注意してください。
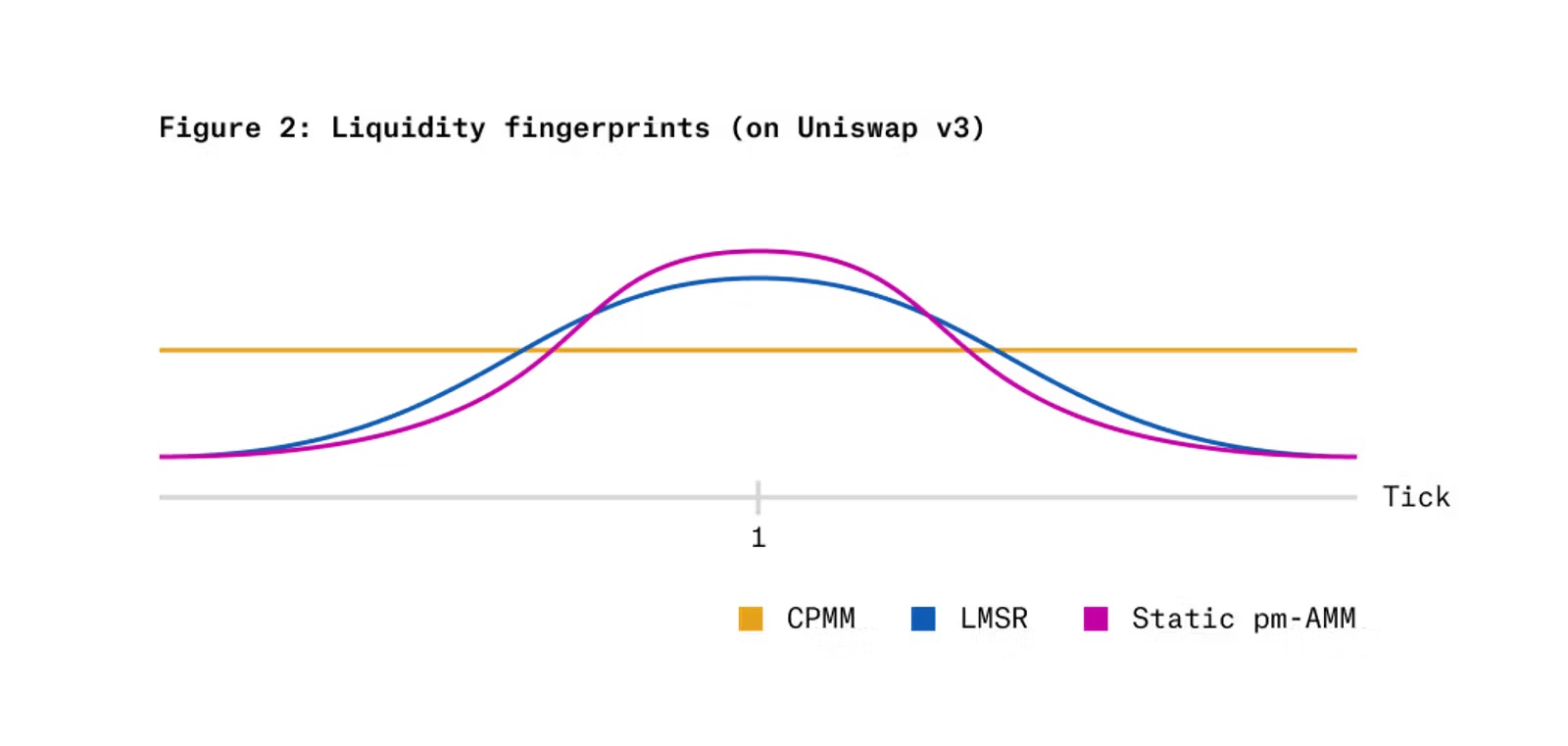
図 2 は、静的 pm-AMM 不変式が Uniswap v3 集中型流動性 AMM に実装された場合に発生する「流動性フィンガープリント」を、CPMM および LMSR と比較して示しています。横軸は相対価格の対数スケール(x トークンの価格を y トークンの価格で割ったもの)に対応し、縦軸はその価格レベルでの各 AMM の流動性に対応します。これら 2 つの代替手段と比較すると、pm-AMM は、相対価格が 1 (確率が 50%、つまりトークン価格が 0.50 に等しい) の場合、より多くの流動性を集中させますが、極端な相対価格 (非常に低いか非常に高い)、流動性の集中度が低くなります。
研究の背景
予測市場
予測市場は、暗号通貨のアプリケーションとしてますます人気が高まっています。 2024 年 10 月だけで、Polymarket の取引高は 20 億ドルを超えました。ただし、暗号通貨の予測市場における流動性のほとんどは AMM ではなくオーダーブックで提供されますが、後者が暗号通貨の DEX 取引量の大部分を占めています。
考えられる理由の 1 つは、生成されたトークンの価格挙動が通常の資産とは異なるため、それらに合わせて設計された AMM が安定的に動作できないことです。例として、誰かがコインを 1001 回投げ、各結果 (表と裏) が 2 つのトークン x と y に対応するコイントス ゲームの予測市場を想像してください。最終的に、表が裏よりも多い場合、x トークンの価値は 1 ドルになり、裏が表よりも多い場合、x トークンの価値は 0 ドルになります。y トークンの場合はその逆が当てはまります。
これらの結果として得られるコインのボラティリティは、残りのトス数と現在のトスに大きく依存します。現在の状況が近づき、残りのトスが少なくなるほど、これらのコインの変動は大きくなります。これは、一定の製品マーケット メーカーの損失 (以下で説明するようにボラティリティに依存します) が時間の経過とともに大きく変化することを意味します。
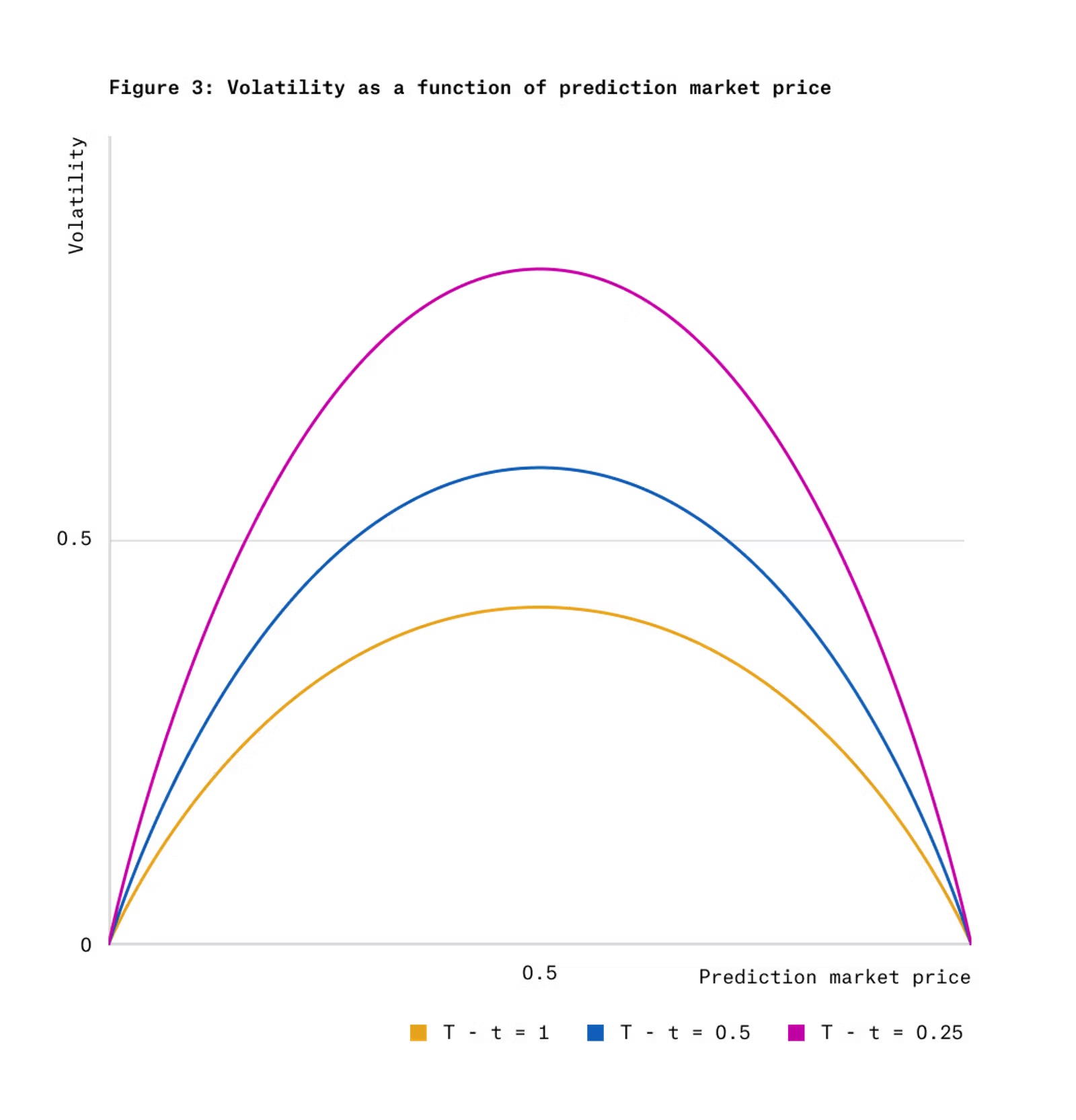
図 3 は、ガウス分数ダイナミクスの下で、トークン価格と残り時間の関数として得られたトークン価格のボラティリティを示しています。
人気のある予測市場の多くは、このコイン投げの例に似ており、将来の有効期限にランダムなトレンドがゼロより上で終わるか下で終わるかに賭けています。例えば:
- バスケットボールの試合結果の予測マーケットでは、試合の残り時間が 0 になるとマーケットは終了します。確率的な動きは 2 チーム間の得点差です。
- 大統領選挙の結果に関する予測市場は投票日に期限切れになります。このうち、確率的動きは、候補者に投票しようとする有権者の数の差です。
- ビットコインなどの資産の価格が将来の特定の日に特定の約定価格よりも高くなるかどうかに関する予測市場では、ランダムな傾向は、現在のビットコイン価格から特定の約定価格を引いた対数になる可能性があります。
この記事で定義するアウトカム トークンの価格変化モデル、つまりガウス分数動的モデルは、そのような例からインスピレーションを得ています。このモデルは、予測された市場価格が、根底にあるブラウン運動がゼロを超えて終了する確率と一致すると仮定します。このモデルは、バイナリー オプションのブラック ショールズ モデルに似ています (バイナリー オプションは、資産の価格が特定の権利行使価格を超えた場合に固定ドル額を支払い、資産価格が特定の権利行使価格を超えた場合に固定ドル額を支払う商品です)資産が特定の権利行使価格を下回っている場合、$0 を支払います)。ただし、私たちのモデルでは、基礎となるプロセスが取引可能な資産の価格に対応する必要はありません。
結果として得られるトークンの価格が 1 ドルである確率と一致するという単純化した仮定を立てます。この仮定は、リスクや時間選好などの市場の重要な特性を無視しているため、これらの特性がこのモデルにどのような影響を与えるかを調べることは、将来の研究の課題となります。
さらに、このモデルは新しい情報が現れる速度が予測可能であることを前提としているため、すべての予測市場がガウス分数動的モデルに適しているわけではないことも理解する必要があります。たとえば、バスケットボールの試合はフットボールの試合よりもこのモデルに適している可能性があります。これは、バスケットボールの試合では得点がはるかに頻繁に記録されるため、時間の経過とともに得点差がより一貫して変化するためです。さらに、一度限りの予期せぬ出来事(地震など)が特定の日付までに発生するかどうかを予測するなど、このモデルとはまったく異なる種類の予測市場もあります。しかし、繰り返しになりますが、このモデルは、他のダイナミクスのモデルを導出するための有用な開始点となる可能性があり、あらゆるモデルの統合 AMM を導出する方法のデモンストレーションとして機能する可能性があります。
損失とリバランスおよび均一性
このモデルを明確にした後、コンスタントプロダクトマーケットメーカーやLMSRなどの既存のAMMよりもこれらのトークンに適している可能性のあるメカニズムを導き出しました。私たちが使用する指標は、流動性プロバイダーの予想損失率であり、損失対リバランスまたは LVR として特徴付けることができます。
LVR は、AMM の主な逆選択コストを取得します。取引がない場合、AMM 価格は静的であり、新しい情報が入手可能になると古くなります。 LVR は、AMM にとって不利な価格で取引を裁定取引する、より知識のある裁定取引者によってこれらの古い価格が利用されるため、AMM 流動性プロバイダーが負担するコストを反映しています。したがって、LVR は、価格を修正するために AMM が裁定取引者に支払う手数料と考えることができます。
さらに、取引手数料がなければ、LVR は、流動性プロバイダーがプール準備金の一部としてまったく同じ数のトークンのショート ポジションを個別に保有することで LP ポジションをデルタ ヘッジすることによって被る損失でもあります。 したがって、LVR は、ブラック ショールズのオプション価格設定モデルの重要な洞察に基づいて構築されています。オプションが原資産とのデルタヘッジによって市場リスクを除去するのと同様に、LVR は市場リスクを除去した後の AMM での LP ポジションを評価します。つまり、LVR は、AMM の準備金と同じトークンを保持するという市場リスクを単に引き受けるのではなく、AMM の流動性プロバイダーであるという特殊性を分離します。
料金や MEV リサイクル メカニズムのない、単純な不変ベースの AMM を検討します。この場合、AMM は裁定取引により確実に損失を被ることになり、AMM の不変条件は LVR を排除できません (トランザクションがまったく発生しない不変条件を除く)。さらに、LVR を「最小化」することさえ実際的な意味はありません。LVR を削減することは、提供される流動性を削減することを意味するだけだからです。
ただし、LVR を排除することはできませんが、プール価値の損失の割合が資産の現在の価格に依存しないように、LVR をより均一にすることはできます。この特性を均一性と呼びます。
スポンサーが、市場が結果として何を予測するかを知るために、手数料ゼロの予測市場に流動性を提供する用意があると想像してください。スポンサーは損失を被ることになりますが、特定の時間や特定の価格に損失を集中させるのではなく、損失を均等に分散させたいと考えます。この場合、資産プールの現在のポートフォリオ価値はスポンサーの「予算」と考えることができます。統合 AMM では、スポンサーがある時点で 1 ドルの流動性を投資した場合、次の時点での予想損失はプールの現在の状態とは何の関係もありません。
さらに、均一性は利益を追求する流動性プロバイダーにとって潜在的な影響を及ぼします。 AMM が損失やリバランスから利益の一部を獲得できたり、(ゼロ以外のスワップ手数料や MEV 税などのオークション メカニズムを通じて)利益を上げることができたとしても、その方法を決定する何らかの戦略が必要になります。異なる価格と異なる時間の性別でフローを割り当てます。ゼロ手数料プールの予想損失は、資産の価格プロセスを考慮した、特定の時点で戦略が割り当てる流動性の量の尺度として考えることができます。
当社では、資産固有の統合 AMM を、資産の現在価格に関係なく、予想される LVR が資産プールの現在価値の一定の割合であるものとして定義します。 AMM が均一の LVR を持つかどうかは、資産自体の価格プロセスに依存することに注意してください。 Milionis et al.の付録 B.2 に示されているように、資産の価格が幾何学的なブラウン運動に従う場合、資産とポジションの間で本質的に唯一統一された AMM は加重幾何平均マーケット メーカーであり、その不変条件は次のとおりです。
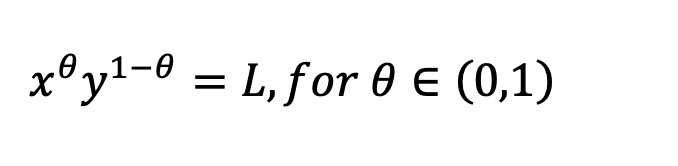
これはバランサーで使用される式であり、Uniswap v2 で使用されるコンスタント プロダクト マーケット メーカーも特殊なケースです。しかし、ガウス分数ダイナミクスに従うトークンの場合、一定の幾何平均 AMM は均一な LVR を持ちません。対数市場スコア ルール (LMSR) についても同様です。
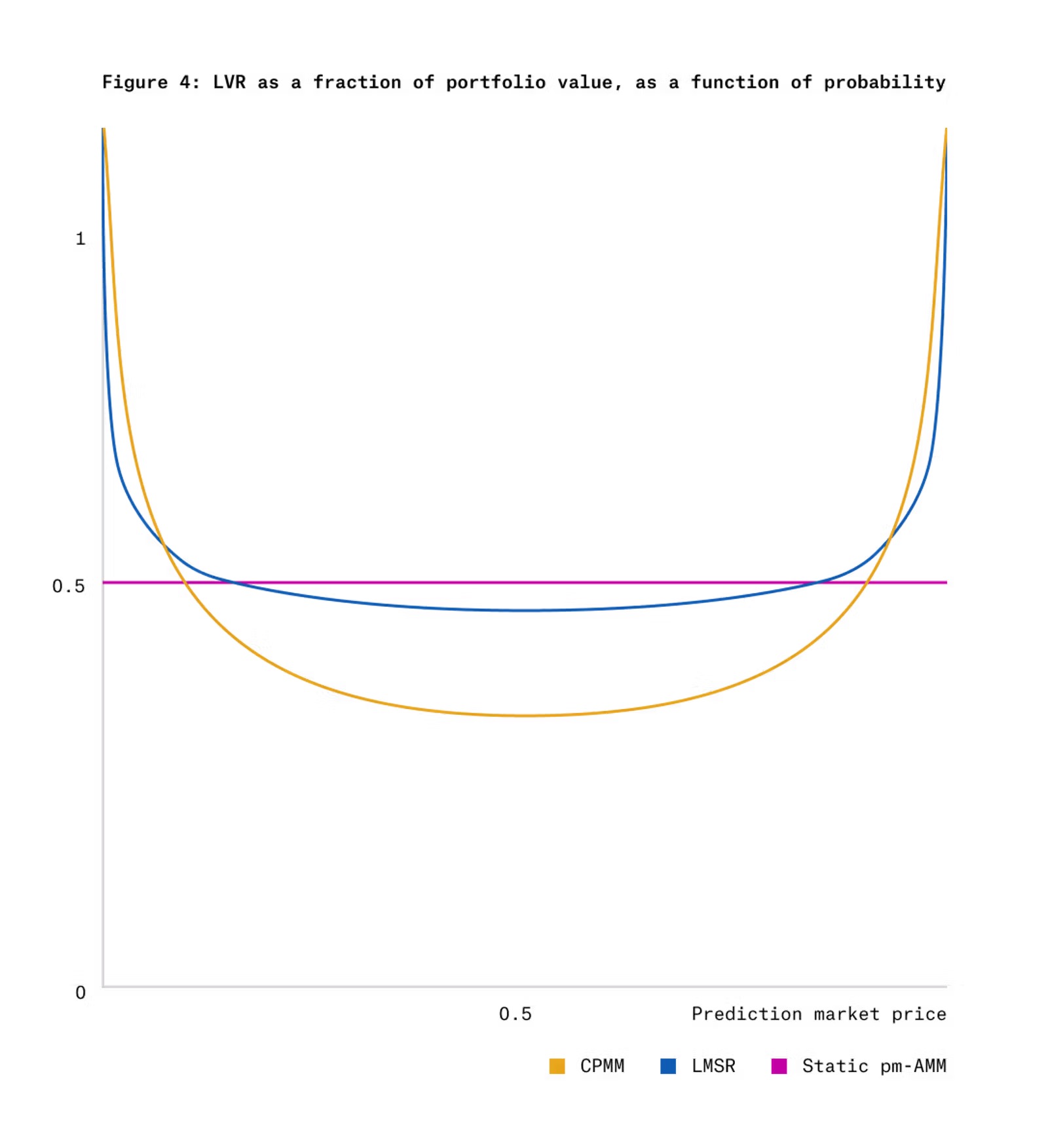
図 4 は、静的 pm-AMM の均一 LVR と比較した、時間 Tt=1 におけるガウス分数動的結果トークンの CPMM および LMSR の LVR を示しています。
これらの考慮事項から、ガウス分数ダイナミクスに基づく予測市場向けに設計された 2 つの AMM を開発しました。1 つは常に均一な LVR を持ちますが、予測市場の有効期限が近づくと LVR は増加します。もう 1 つは均一な LVR を持ちます。残りの時間枠全体で一定の予想 LVR が得られます。
図 4 からわかるように、結果として得られるトークン価格がゼロまたは 1 に近い極端な場合、CPMM と LMSR の LVR は大きくなります。これは、これらのポイント付近では価格変動性が低い一方で (図 3 を参照)、極端な価格では資産プールの価値がより速く減衰するためです。したがって、統合 AMM は極端な価格での流動性を低くする必要があり、これはまさに pm-AMM 設計が行うことです (図 2 を参照)。
これまでの研究
AMM は、予測市場と市場スコアリング ルール (LMSR など) に由来します。これらのルールは、Uniswap v2 などの定数関数マーケット メーカー (CFMM) の発見につながりました。CFMM は、多くの場合、各資産の AMM の準備金間の不変関係によって特徴付けられます。この設計に基づくAMMは、近年のDEXの主流の市場メカニズムとなっています。
最近では、金融経済学の観点が、主に幾何学的なブラウン運動に焦点を当て、損失とリバランス (LVR) の形で自動マーケット メーカーのコストを理解するために適用されています。一方、予測市場の価格動向は、リターンと期間が限られているため、大きく異なります。 Taleb は、基礎となる観察可能な投票プロセスに基づいたダイナミクスを提案しましたが、私たちは基礎となる観察可能なガウス分数プロセスに基づいた別のダイナミクスを開発しました。
非GBM資産の自動マーケットメーカーの設計に関する応用研究はこれまでにいくつか行われています。一例として、ステーブルコインペア用に設計された AMM である StableSwap は、関連資産と平均回帰資産の間の自動マーケットメーカーが流動性を 1 つの価格に厳密に集中させる必要があるという直感的な前提に基づいていますが、その導出には資産価格プロセスのモデル化は含まれません。もう 1 つの例は、ゼロクーポン債券用に設計された AMM である YieldSpace です。 YieldSpace の導出には、単純なゼロクーポン債券価格設定モデルが含まれていますが、完全な価格プロセス モデルは含まれていません (金利の推移はモデル化されていません)。
さらに、学界では、資産価格の動きに関する信念に基づいてリアルタイムの市場モデルを設計する研究がいくつか行われています。一例は、Goyal らによる設計です。彼らのフレームワークは、予想される損失を調整するのではなく、予想されるアクティブ流動性を最大化することを中心に設計されているため、場合によっては私たちのフレームワークとは逆の結果をもたらします。たとえば、彼らの導出は、流動性プロバイダーが資産の相対価格が 1 付近にとどまると予想する場合、LMSR (CPMM と比較して価格 1 付近に流動性を集中させる) が適切であることを示唆していますが、価格の乖離が(結果トークンの場合のように) 予想される場合、流動性を 1 付近に集中させるのが理にかなっています。
さまざまなAMMモデル
自動マーケットメーカー
単一のイベントの予測市場と、2 つの競合する資産を取引する AMM を考えることができます。リスク資産の 1 つは、 AMM は不変 f(x,y)=L を維持します。ここで、f(⋅,⋅) は埋蔵量 (x,y) の不変関数であり、L は定数です。資産 x の価格 P (米ドル) が与えられると、資産プールの価値関数は次のようになります。
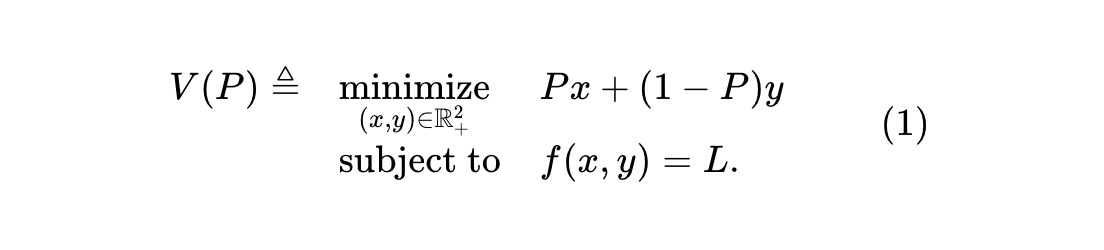
これは、x の価格が P の場合の資産プールの価値です。資産 x と y をそれぞれ 1 単位保有することは現金を保有することと同等であるため、y の価格を 1-P とする必要があります。各時刻 t での資産 x の価格 Pt (および資産 y の価格 1-Pt) を観察できる裁定取引者のグループが存在すると仮定します。取引手数料やその他の摩擦がないと仮定すると、これらの裁定取引者は継続的に AMM を監視し、AMM の誤った価格設定から価値を引き出そうとします。自らの利益を最大化するために、彼らは AMM 準備金の価値を最小限に抑えるために AMM と取引します。時刻 t での準備金 (価格が Pt のとき) を Vt で表すと、Vt = V(Pt) となります。
例 1: コンスタント プロダクト マーケット メーカー (CPMM) の場合、不変式は f(x,y)≜xy であり、資産プール価値関数は次のとおりです。
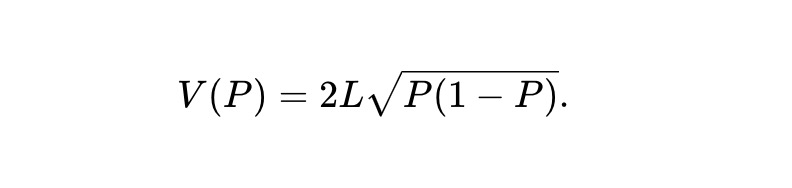
例 2: Robin Hanson によって作成された対数市場評価ルール (LMSR) は、次の不変条件を満たす AMM として見ることができます。
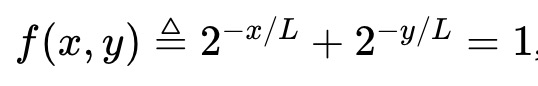
その資産プールの価値関数は次のとおりです (価格によって暗示されるイベントのバイナリ エントロピーに比例します)。
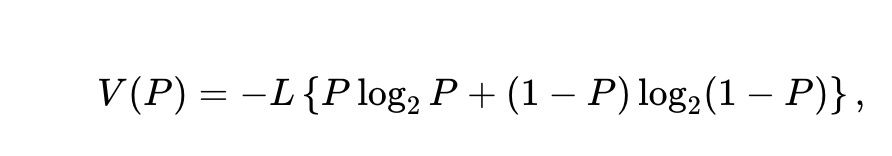
最適化問題 (1) の最適解を 1 で表しますが、現在の環境の場合は次のようになります。
定理 1. すべての価格 P≥0 について、資産プールの価値関数は次の条件を満たします。
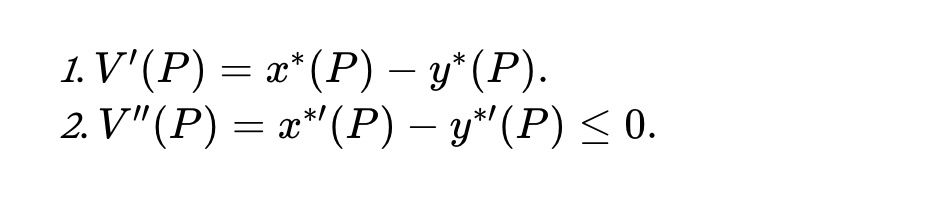
ガウス分数ダイナミクス
ガウス分数ダイナミクスと呼ばれるものに基づいて、リスク資産の価格は時間の経過とともにどのように変化するのでしょうか?具体的には、時間間隔 t∈[0,T] に確率過程 {Zt} が存在すると仮定します。ここで、イベントは時間間隔 t=T の終わりにおける Zt の符号によって決定されます。 ZT≥0 の場合、次に x 資産の払い戻し、ZT < 0 の場合、y 資産が払い戻されます。 Zt は、二国間競争における 2 つのチーム間のポイント差として理解できます。したがって、Zt をスコアリングプロセスとみなします。私たちのモデルはこの部分的なプロセスの存在を前提としていますが、AMM はこれらのプロセスを直接観察する必要がないことに注意してください。以下で説明するように、AMM は限界価格 (裁定取引後) と有効期限に基づいて端数の現在価値を推測できます。
Zt はランダムな変動に従うと仮定します。具体的には、Zt はボラティリティ σ>0 のブラウン運動、つまり dZt=σdBt であると仮定します。ここで、Bt は標準ブラウン運動です。したがって、時刻 t における資産 x の価格 Pt が次のようになることがわかります。
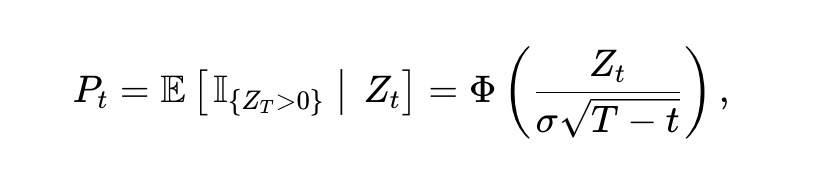
このうち、Φ(⋅) は標準正規累積分布関数 (CDF) です。 Itô の定理を適用すると、Pt は次を満たさなければなりません。
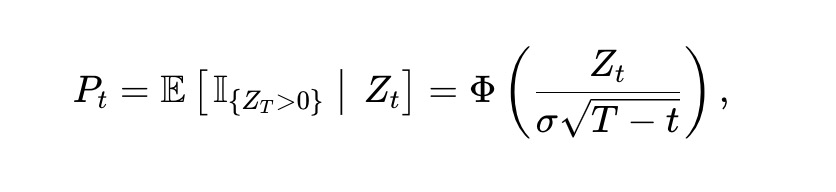
このうち、ϕ(⋅) は標準正規確率密度関数、Φ-1(⋅) は逆 CDF です。分数のダイナミクスと分数から価格への変換、またはその逆の変換は σ に依存しますが、分離された価格プロセス Pt のダイナミクスは σ に依存しないことに注意してください。これらの動的な変動を価格と残り時間の関数として図 3 に示します。
統合 AMM
上記の議論によれば、時刻tにおける資産プール準備金の価値をVtで表すと(このときの価格はPt)、Vt=V(Pt)となる。伊藤の定理を適用すると、資産プールの価値は次の式に従って変化すると結論付けることができます。
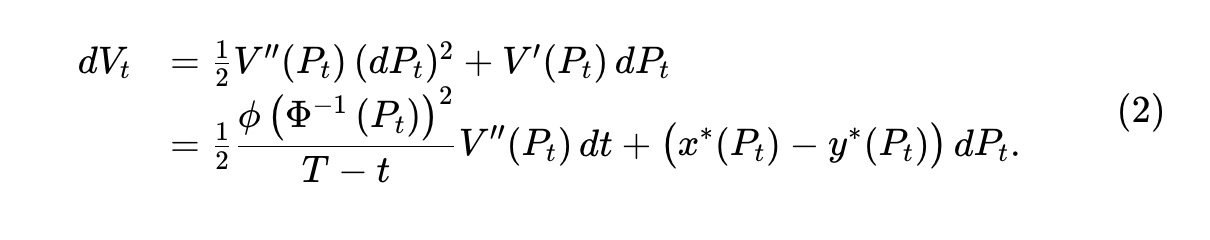
価格 Pt はマーチンゲールであるため、(2) の第 2 項もマーチンゲールであり、増加または減少している可能性があります。ただし、V(⋅) (定理 1 を参照) によれば、最初の項は負の変換に対応するため、減少過程になります。これはミリオニスらによって提案された損失とリバランスのプロセスであり、不利な価格で資産プールをヘッジする裁定取引者によって失われた価値を捕捉します。この損失の瞬間レートを次のように定義します。
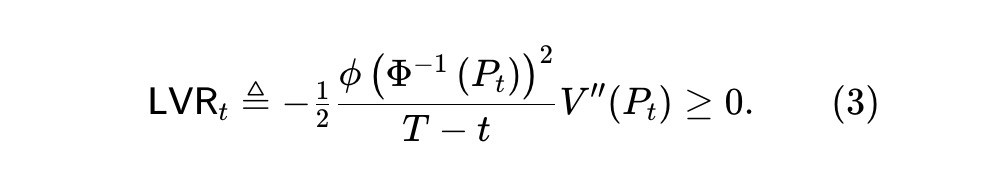
Milionis らは、幾何学的なブラウン運動に従う資産の場合、基本的に幾何平均マーケット メーカーのみが統合 AMM であることを発見しました。ガウス分数ダイナミクスに基づく予測市場では、(3) を調べるために、統合 LVR プールは次の常微分方程式 (ODE) を解く必要があります。
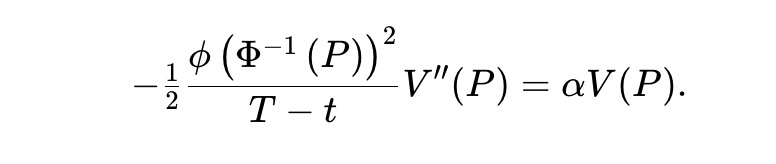
方程式の左側は t に依存しますが、右側は依存しないため、これは不可能です。ここでの中心的な問題は、幾何学的なブラウン運動の力学は時間にわたって不変であるのに対し、ガウス分数運動の力学は時間に大きく依存するということです。
この問題を回避するために、α を時間に関連付けることができます。つまり、α=β/(Tt) (β>0) を設定し、そのような設定を検討します。
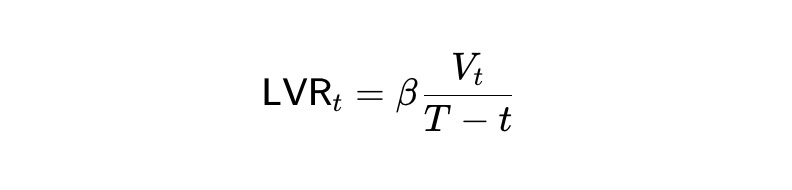
これは、P≥0 の ODE と同等です。さらに、V(⋅) には、V''(P)≤0 などの追加の要件があります (定理 1 を参照)。
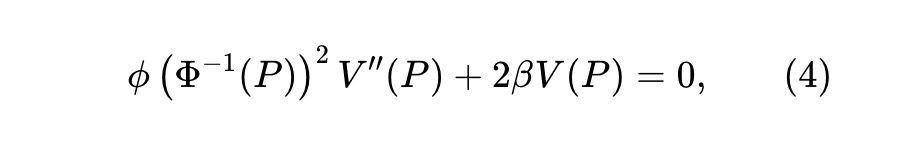
静的 pm-AMM
上記の ODE は、変数 u=Φ-1(P) を変更することで簡略化できます。 β=1/2 の場合、ODE と追加の凹面要件の両方を満たす解があり、その値は次のとおりです。

x および y トークンの予備量は次のとおりです。
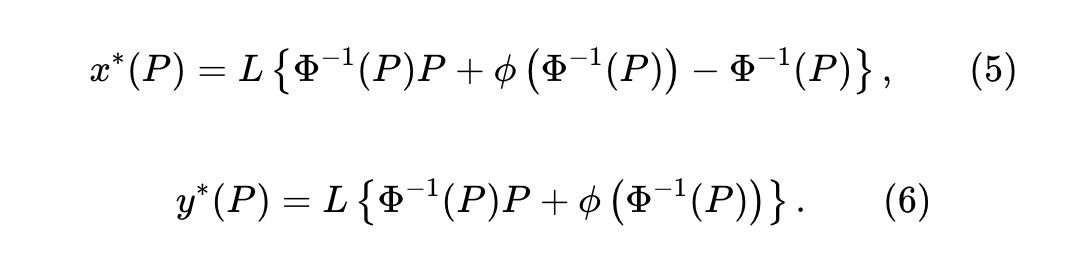
ここで、L≥0 は資本プールのサイズのスケーリングを決定する流動性パラメーターです。 y∗(P)-x∗(P)=LΦ-1(P) を観察し、それを (5) に代入すると、資金プール準備金 (x, y) は次の不変式を満たす必要があります。
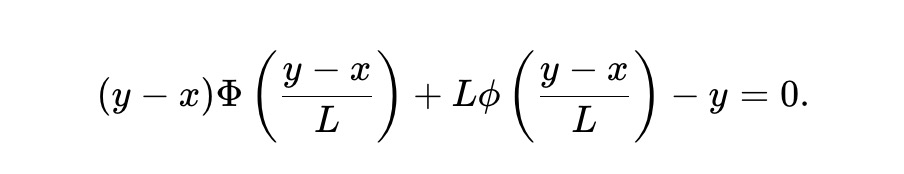
これは静的 pm-AMM の定義です。設計によれば、AMM は次の関係を満たします。
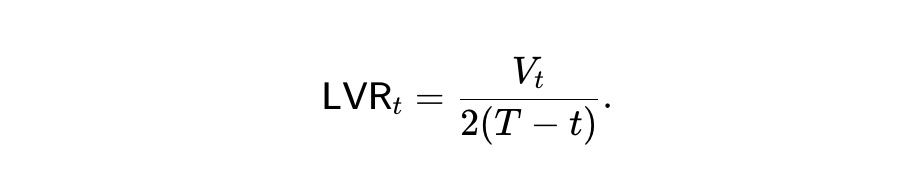
Vˉt=E[Vt] をプールの期待値として定義します。(2) から次のように導出されます。
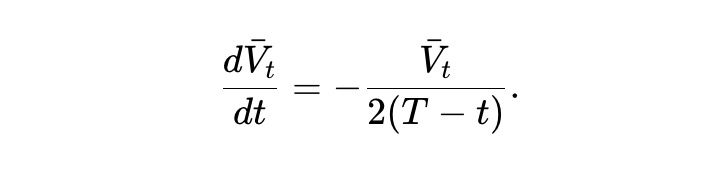
この常微分方程式を解くと、次の答えが得られます。言い換えれば、予想される条件下では、静的 pm-AMM の資産プール価値は、残りの期間の平方根に従って減衰します。
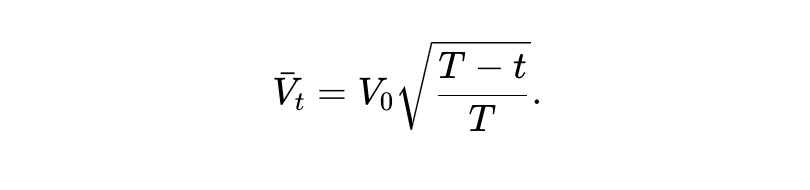
動的pm-AMM
静的 pm-AMM の欠点の 1 つは、ドルあたりの LVR 値がすべての可能な価格にわたって均一であるにもかかわらず、時間の経過とともに変化することです。特に、価値の 1 ドルあたりの損失は有効期限に反比例するため、有効期限時にすべての価値が失われるまで時間の経過とともに増加します。
動的な流動性。私たちは、AMM LP が時間の経過とともに流動性を抽出して損失を削減する、静的な pm-AMM 設計の動的な時間変形を想定しています。具体的には、資本プールの値が次のようになっていると仮定します。
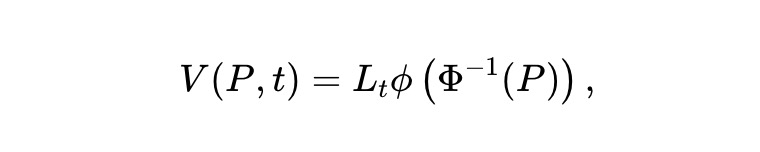
ここで、Lt は、時間の経過とともに流動性がどの程度除去される (または追加される可能性がある) かを決定する決定論的な滑らかな関数です。伊藤の定理を資産プール価値プロセス Vt≜V(Pt,t) に適用すると、
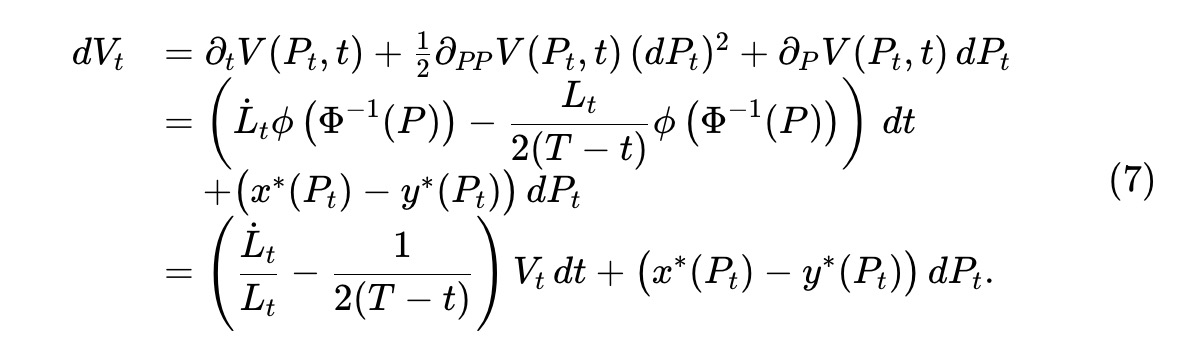
Ct を引き出した流動性の累積ドル価値を表すものとします。プール価値は流動性 Lt に線形関係があるため、Lt の変化のドル価値は Vt/LT に正比例します。次のものを取得できます。
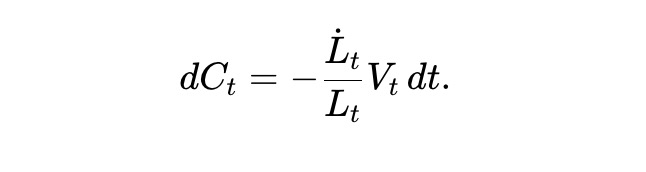
AMM LP の総資産 Wt は、資金プールの準備金と引き出した流動性の累積値で構成され、Wt=Vt+Ct となり、次の条件を満たします。
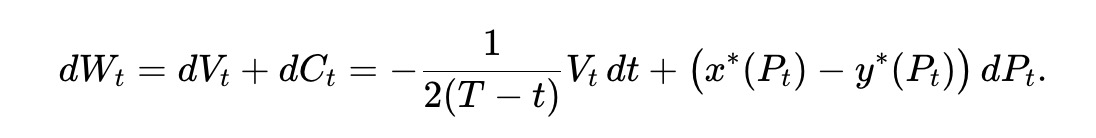
これは、LP の期待富 Wˉt≜E[Wt] が次の条件を満たすことを意味します。ここで、Vˉt≜E[VT]。
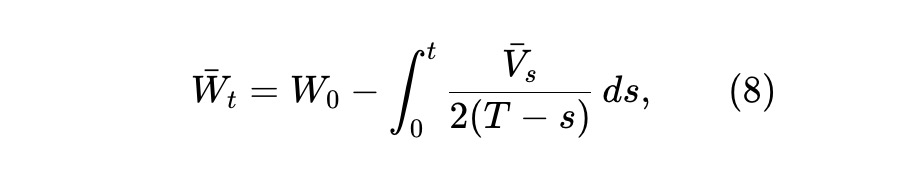
ここで、次のように流動性曲線の具体的なオプションを検討してください。
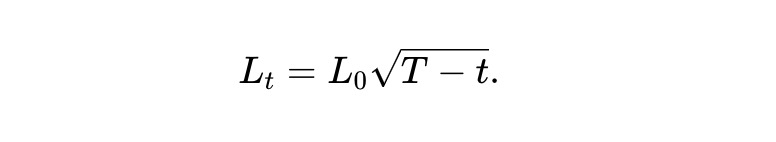
これを動的 pm-AMM と呼びます。 (7) によれば、資産プールの期待値 Vˉt=E[Vt] は次の条件を満たします。
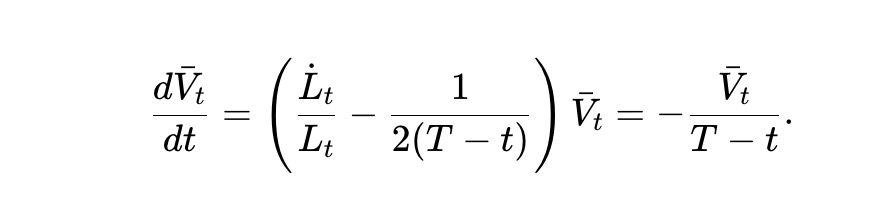
この常微分方程式を解くと、次の答えが得られます。
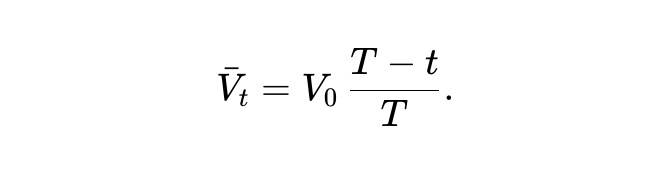
言い換えれば、動的pm-AMMでは、引き出し後に期待プール値は直線的に減少します。さらに、静的 pm-AMM の価値関数を継承しているため、単位時間あたりの LVR 損失率は次のようになります。
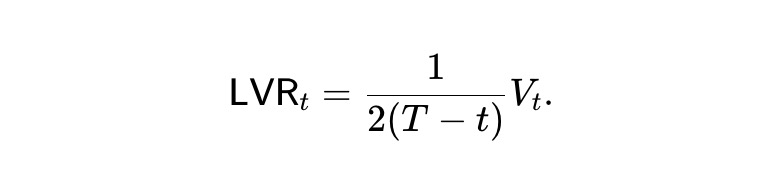
期待損失率は以下の値であり、期間 t の間一定です。つまり、動的な pm-AMM は、時間の経過とともに一定の割合 (期待) で裁定取引者の資金を失います。
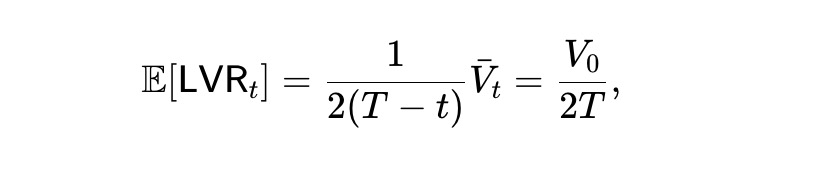
最後に、(8) より、下図のような期待富の過程が得られます。したがって、最初の富の半分は最終的には失われます。
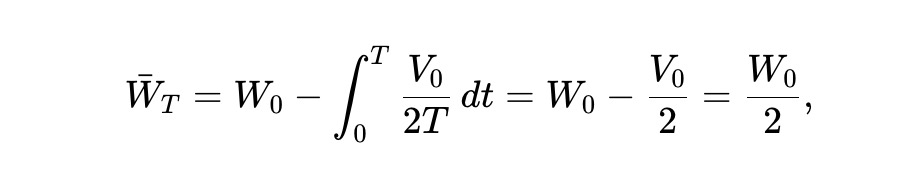
結論は
pm-AMM は、ガウス分数動的モデルなどのダイナミクスによって駆動される予測市場に適している可能性があります。これに加えて、私たちの調査では、統合 AMM が債券、オプション、その他のデリバティブなどの他の種類の資産にも適している可能性があることも示しています。





