统计分析是在一堆独立的、自身没有实际意义的数据中寻找可能存在的趋势、分布、概率等有意义的信息。统计学的目标是探索和把握数据内在的规律。统计学的应用,简单来说就是通过搜集相关数据并进行整理和分析,然后根据数据做出决策。掌握统计学,对日常生活决策也有很大帮助。比如,“十赌九输”几乎是人人都知道的基本常识,但所有的赌徒都乐此不疲,原因是都认为自己是那极少数的赢家,都想让“赢”这一小概率事件发生在自己身上,从而一夜暴富。
统计的基本方法有以下几点:
1)根据历史数据,猜测背后的规律
2)基于假设,建立模型,用于描述规律
3)用样本统计量分布来估计模型参数
4)用历史数据来检验模型假设
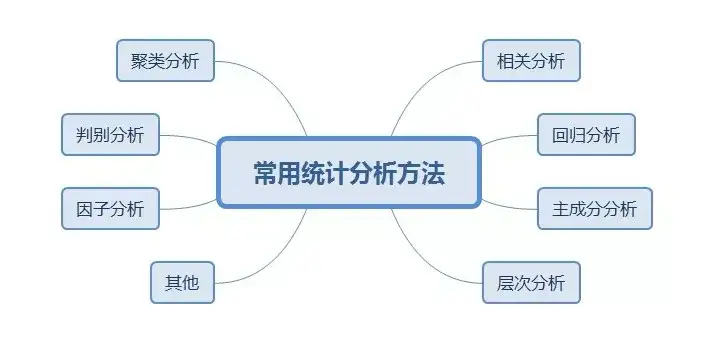
常用的统计分析方法有下面这几种:
统计在经济领域的应用非常广泛,微观层面,像企业对所售产品的定价决策、市场行情与判断、市场竞争力都需要进行统计分析;宏观层面,短期经济形势分析和预测判断通常也都是建立在对经济统计指标数据分析的基础之上的。除此之外,国家经济结构变化、国内外贸易动态、金融证券投资等领域也都离不开统计分析。
随着金融行业的繁荣与发展,以及金融工具的不断创新发展,金融市场的复杂程度在不断加大,统计学在金融领域的应用越来越受到重视。金融是一门立足于经济现象之上的学科,与统计学之间有着千丝万缕的联系。越来越多的统计方法被用于金融数据分析和金融市场研判。

如上图所示,统计学的知识体系涵盖了很多的内容,考虑到本课程的难度和在金融市场中的实用价值,这里我们主要介绍正态分布和分位数以及它们在金融领域的应用。
正态分布
在介绍正态分布之前,先来看一下什么是概率分布。
如果我们想要准确的预测一个变量,我们首先要了解这个变量的基本行为。我们要确定目标变量可能的输出结果,以及这个输出结果是离散的还是连续的。以骰子为例,我们首先要知道它可以有的取值范围,也就是1到6的整数值。下一步就是为事件分配概率。概率越高,事件发生的可能性就越大。当我们大量重复进行实验得到变量的输出值,就可以根据这些值作图,得到的曲线就是概率分布曲线。目标变量的值的概率就是这一变量的概率分布。
正态分布作为一种特殊的概率分布,不仅曲线优雅,而且在自然界中无处不在,让你在纷繁的数据背后看到缜密的秩序。
“神说,要有正态分布,于是就有了正态分布;神觉得正态分布不错,就让随机误差服从了正态分布。”
正态分布是一种非常常见的连续概率分布,常被用在自然科学等领域来表示一个不明的随机变量:
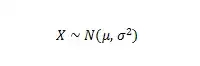
正态分布的密度函数曲线是中间高两边低,由中间向两边递减,并且左右对称,是一条光滑的 “钟形曲线”:
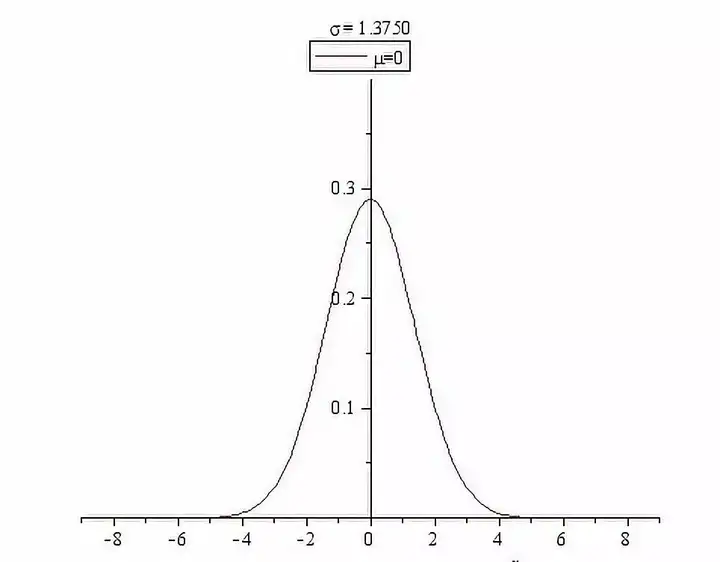
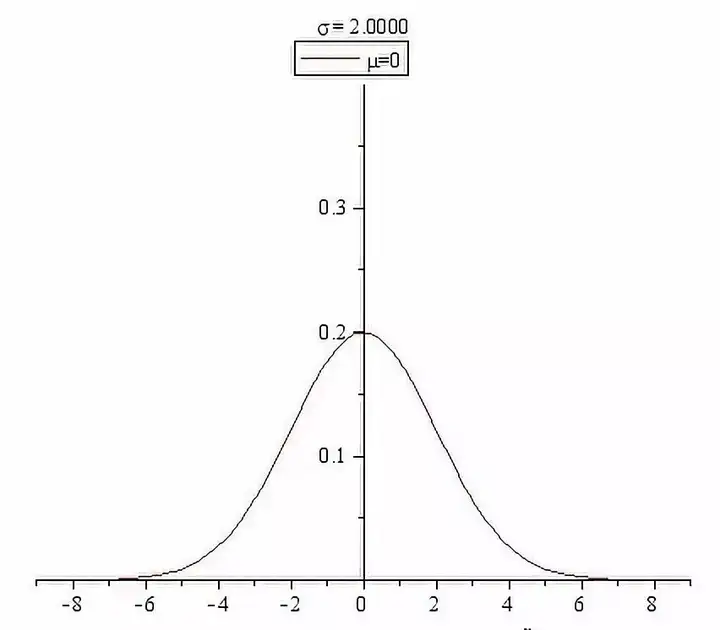
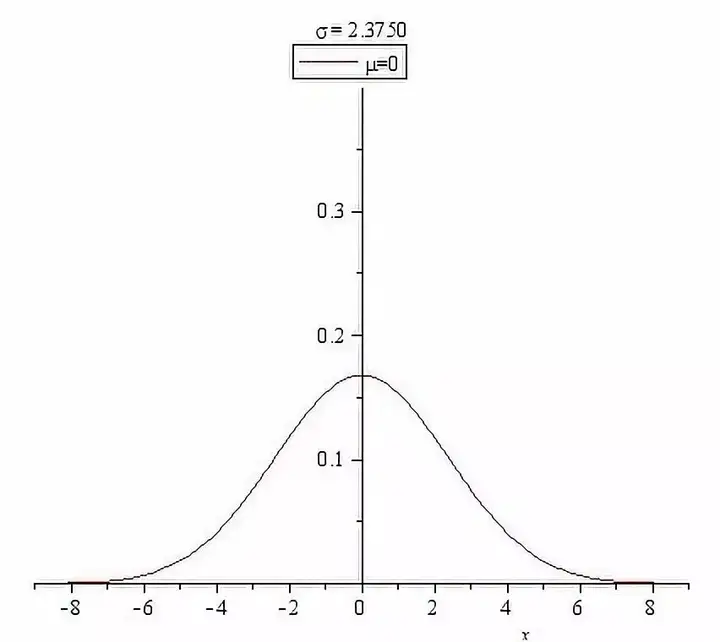
正态分布距离均值越近的地方数值越集中,距离均值越远的地方数值越稀疏;这意味着正态分布出现极端值的概率很低,而出现均值附近的数值的概率非常大。
正态分布的密度函数如下:
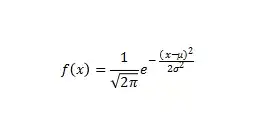
其标准化后的概率密度函数为:
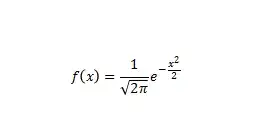
正态分布有以下特性:
集中性:正态曲线的高峰位于正中央,即均数所在的位置;
对称性:正态曲线以均数为中心,左右对称,曲线两端永远不与横轴相交;
均匀变动性:正态曲线由均数所在处开始,分别向左右两侧逐渐均匀下降。
正态分布又被称为高斯分布。德国的10马克纸币上有高斯的头像和正态密度曲线:

正态分布在统计中是非常常用的分布,例如在医学上,可以应用正态分布估计人体的某些生理指标,比如白细胞数的正常值范围,白细胞数在正常人群中近似服从正态分布。此外,各种各样的心理学测试分数和物理现象比如光子计数都被发现近似地服从正态分布。
在金融数据的分析中,很多情况下我们会假设数据满足正态分布,例如证券的收益率和价差等。 在一些量化交易策略中,正态分布也为我们提供了许多便捷,例如很多配对交易策略,就是以证券对之间的价差变化服从正态分布为假设前提的。
借助万矿量化平台,利用正态分布假设,我们可以实现一个较为简单的期货套利策略:
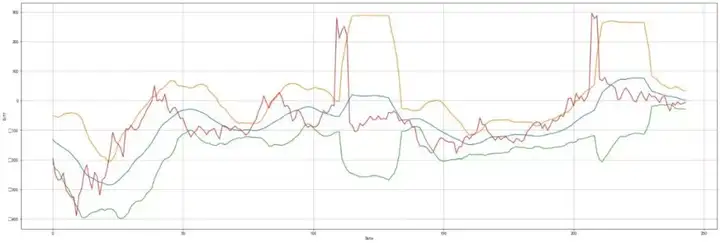
首先假设期货的价差服从正态分布,可以利用其涨跌幅的相关性进行套利。由于螺纹钢和热轧卷板的走势存在较强的相关性,我们使用螺纹钢和热轧卷板的数据,绘制其收盘价差以及上下轨:
这部分的代码如下:

我们简单的在价差上穿上轨线时做多螺纹,做空热卷;在价差下穿下轨线时做空螺纹,做多热卷,价格触及均线时,清空仓位。这个策略的回测结果如下:
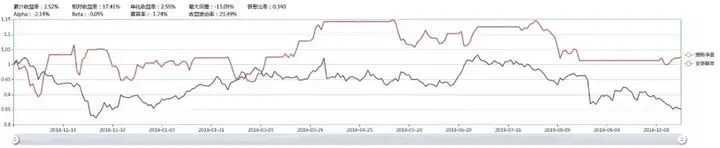
可以看到,这个策略的年化收益率为2.59%。
有关交易策略和量化实现的内容我们在ALPHA Library的高级课程中会具体讲解,这里仅作为了解。
分位数
分位数的英文名称是Quantile,是指将一组数据划分为成一定比例的数值点,常用的有中位数、四分位数、百分位数等。把一组数据进行排序,然后取25%位置、50%位置、75%位置或是其他位置的数据,就成为分位数。
众数、中位数、分位数、均值、几何平均数、切尾均值都是表征集中趋势的指标。当数据分布在偏度上偏离正态分布时,算术平均数、中位数、众数之间有这样的特征:右偏时:算术平均数>中位数>众数;左偏时:众数>中位数>算术平均数。正态分布情况下众数、中位数、算术平均数相等。
分位数存在的意义在于,当数据存在偏态的时候,只看数据的中间位置略有不妥,希望同时保有中位数稳健的特性,又要对“中间”进行修正,可以使用25%或是75%分位数,通过这两个分位点的数据来判断总体水平。
分位数在生活中有很多应用场景。例如在考试的排名中, 如果75%分位数是80分,这就意味着80分以上的同学能够排进前25%。再比如在讨论一个城市的平均工资时,高收入的人群其收入远大于低收入的人群,就会出现“被平均”的现象,于是使用分位数是比较好的选择,使用分位数可以清晰的看到你的工资水平处于前百分之几,也就是比这个城市中多少人高,而不是简单的和“被平均”的平均工资比较。
在金融研究领域,分位数回归在股票、期货的风险测量和演化模式分析、IPO定价行为、基金流量决定因素分析、CAPM模型、高频金融数据价量关系、资本结构选择等方面频繁使用。
在金融市场中,分位数也是一个简单而实用的工具。如果要衡量市场上全部基金的表现进而挑选合适的基金时,可以使用分位数,比如90%分位数,这样挑选出来的基金就是在业绩上打败了90%的其他基金。在进行指数基金定投时,如果指数PB低于历史某个分位数的时候,可以加大定投的力度。
统计学其他理论方法在金融中的应用
通过协整检验、ECM模型 、非平稳时间计量经济模型、VaR模型等的运用,统计学对我国货币政策效率、货币供给对产出和价格的影响、人民币汇率波动造成的物价水平波动、相关财政政策和货币政策刺激经济增长原理分析等宏观数据的实证研究做出了不小的贡献。
用统计方法研究金融市场比较典型的是VaR的运用和具有异方差的时间序列模型技术的应用。近年来,神经网络等机器学习在金融市场中的应用也越来越多。
统计学的理论方法不是最重要的,我们需要养成提出假设、将实际应用问题抽象为数学问题、并能进行分析验证的统计思维。














