撰文:Vitalik Buterin
编译:Yangz,Techub News
以太坊协议设计中有很多「小设计」对以太坊的成功至关重要,但却无法很好地归入一个更大的子类别。在实践中,大约有一半的内容是关于各种 EVM 改进的,其余的则是各种小众话题。本文就将探讨这部分话题。
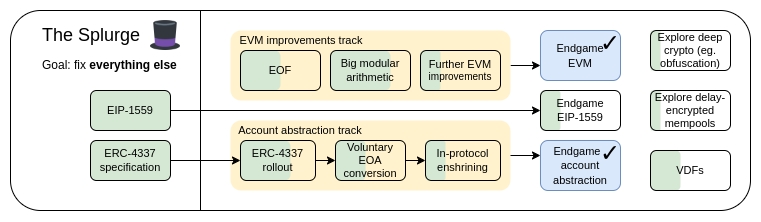
The Splurge 的主要目标:
-
使 EVM 达到性能稳定的「最终状态」
-
在协议中引入账户抽象,使所有用户都能从更安全、更便捷的账户中受益
-
优化交易费用经济学,提高可扩展性,同时降低风险
-
探索先进的加密技术,使以太坊从长远来看变得更好
改进 EVM
改进 EVM 旨在解决什么问题?
目前的 EVM 难以进行静态分析,因此难以创建高效的实现方法、正式验证代码并随着时间的推移进行进一步扩展。此外,它的效率极低,因此很难实现多种形式的高级加密技术,除非通过预编译明确支持这些技术。
如何改进 EVM?
当前 EVM 改进路线图的第一步是EVM 对象格式(EOF),计划在下一次硬分叉中引入。EOF 是一系列 EIP,它规定了新版本的 EVM 代码,具有许多显著特点,其中最突出的包括:
-
代码(可执行,但无法从 EVM 读取)与数据(可读取,但不可执行)分离
-
禁止动态跳转,只允许静态跳转。
-
EVM 代码不再遵从与 gas 相关的信息。
-
新增显式子程序机制。

EOF 代码框架
尽管最终有可能废除旧式合约(甚至可能强制转换为 EOF 代码),但旧式合约将继续存在并可创建。新式合约将受益于 EOF 所带来的效率提升,包括因子程序功能而略微缩小的字节码,以及 EOF 特有的新功能或其特有的 gas 成本缩减。
引入 EOF 后,进一步升级将变得更加容易。目前最完善的是EVM 模块化算术扩展(EVM-MAX)。EVM-MAX 专门为模块化算术创建了一组新的操作,并将其置于一个新的内存空间,其他操作码无法访问。这样,就可以使用蒙哥马利乘法(Montgomery multiplication)等优化运算。
一种较新的思路是将 EVM-MAX 与单指令多数据(SIMD)功能相结合。从Greg Colvin 的 EIP-616开始,SIMD 作为以太坊的一个小设计已经存在了很长时间。SIMD 可用于加速多种形式的加密算法,包括哈希函数、32 位 STARK 和格密码。EVM-MAX 和 SIMD 是对 EVM 性能导向型扩展的天然组合。
组合式 EIP 的大致设计思路是,以EIP-6690为起点,然后:
-
允许任何奇数或任何 2 的幂至(2768)作为模数
-
为每个 EVMMAX 操作码(
add,sub,mul)添加一个版本,该版本不再取 3 个直接值(x/y/z),而是取 7 个直接值(x_start、x_skip、y_start、y_skip、z_start、z_skip、count)。在 Python 代码中,这些操作码将执行相当于以下的操作:

-
但在实际执行中,这些操作码将被并行处理
-
有可能的话,可以增加
XOR、AND、OR、NOT和SHIFT(循环和非循环),至少对二乘以二的模数来说是这样。此外,还可添加ISZERO(将输出推入 EVM 主堆栈)
这样就足以实现多种形式的加密算法,包括椭圆曲线加密、小域加密(如 Poseidon、circle STARKs)、传统哈希函数(如 SHA256、KECCAK、BLAKE)和格密码。
当然,其他 EVM 升级也是可能的,但迄今为止,它们受到的关注要少得多。
现有的相关研究
还有哪些工作要做,如何权衡?
目前,EOF 计划被纳入下一个硬分叉。虽然计划总有被移除的可能(此前就有过在最后一刻将计划从硬分叉中移除的情况),但这么做会是一场艰苦的「战斗」。移除 EOF 意味着未来对 EVM 的任何升级都不需要 EOF,这是可以做到的,但可能会更困难。
EVM 的主要权衡在于 L1 的复杂性与基础设施的复杂性。要在 EVM 实现中添加 EOF,需要大量代码,而且静态代码检查也相当复杂。不过,作为交换,我们可以简化高级语言、简化 EVM 实现并获得其他好处。这么说吧,一个优先考虑持续改进以太坊 L1 的路线图将包括并建立在 EOF 的基础上。而其中的一项重要工作是实现类似 EVM-MAX 加 SIMD 的功能,并对各种加密操作需要耗费多少 gas 进行基准测试。
对路线图的其他部分有何影响?
在 L1 调整其 EVM 后,L2 可以更容易地进行复刻。一方调整而另一方不调整,会导致不兼容,而这也有其自身的弊端。此外,EVM-MAX 加上 SIMD 可以降低许多验证系统的 gas 成本,从而提高 L2 的效率。用 EVM 代码取代预编译代码,也许不会对效率造成太大影响,但却能执行相同的任务,从而更容易移除更多的预编译。
账户抽象
账户抽象旨在解决什么问题?
如今,交易只能通过一种方式验证,即 ECDSA 签名。账户抽象的初衷是在此基础上进行扩展,使账户的验证逻辑可以是任意的 EVM 代码。这样就能实现一系列应用,包括:
-
转用抗量子加密技术
-
淘汰旧密钥(普遍认为这是一种值得推荐的安全做法)
-
多签钱包和社交恢复钱包
-
低价值操作使用一个密钥签名,高价值操作使用另一个密钥(或一组密钥)签名
-
允许隐私协议在没有中继器的情况下运作,从而大大降低复杂性,并消除关键的核心依赖点
自 2015 年开始对账户进行抽象以来,这些目标已扩展成一大套「便捷目标」,例如一个没有 ETH 但有其他 ERC20 代币的账户可以用这些代币支付 gas 费。下图是这些目标的一个总结:
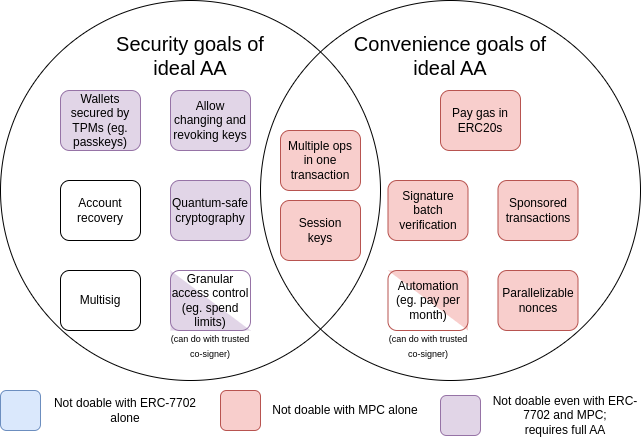
MPC 指的是多方计算,这是一种已有 40 年历史的技术,可将密钥分割成多个片段存储在多个设备上,并使用加密技术生成签名,而无需直接合并密钥片段。
EIP-7702是计划在下一次硬分叉中引入的 EIP,也是人们日益认识到有必要让包括 EOA 用户在内的所有用户都能享受到账户抽象带来的便利,从而在短期内改善用户体验,并避免分裂成两个生态的结果。这项工作始于EIP-3074,并在 EIP-7702 中达到高潮。EIP-7702 使账户抽象的 「便捷功能」适用于所有用户,包括现在的 EOA(外部账户,即由 ECDSA 签名控制的账户)。
从图表中我们可以看出,虽然某些挑战(尤其是关于「便捷性」的挑战)可以通过多方计算或 EIP-7702 等增量技术来解决,但促使最初提出账户抽象建议的大部分安全目标只能通过回溯并解决最初的问题来解决,即允许智能合约代码控制交易验证。目前还没有做到这一点是因为安全实现这一目标仍是一项挑战。
账户抽象如何运作?
账户抽象的核心是允许智能合约而不仅仅是 EOA 发起交易,其复杂性来自于如何以有利于维护去中心化网络和抵御拒绝服务攻击的方式实现这一点。
多重验证问题是一大关键挑战:
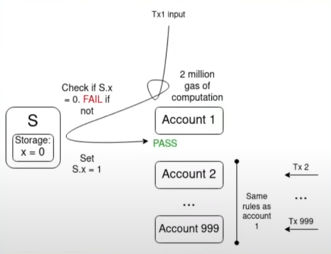
假设有 1000 个账户,其验证功能都取决于某个单一值S,而 mempool 中的交易在S的当前值下都是有效的,那么单个翻转S值的交易就会使 mempool 中的所有其他交易失效。这样,攻击者就能以极低的成本向 mempool 发送垃圾邮件,堵塞网络上的节点资源。
多年来,我们一直在努力扩展功能,同时限制 DoS 风险,最终,我们就如何实现「理想的账户抽象」达成了共识,提出了 ERC-4337。
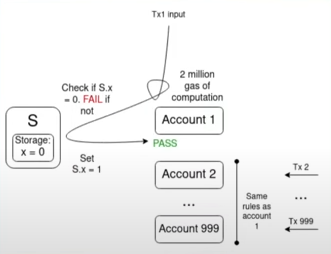
ERC-4337 将用户操作的处理分为两个阶段,即验证和执行。首先处理所有验证,然后处理所有执行。在 mempool 中,只有当用户操作的验证阶段只涉及自己的账户,且不读取环境变量时,该用户操作才会被接受。这可以防止多重验证攻击,也会对验证步骤执行严格的 gas 限制。
ERC-4337 被设计为协议外标准(ERC),因为当时以太坊客户端开发者正忙于合并(the Merge),没有多余的能力开发其他功能。而这也是 ERC-4337 使用用户操作作为对象,而不是常规交易的原因。不过,最近我们意识到,至少有必要在协议中加入 ERC-4337 中提出的部分功能。两个主要原因是:
-
EntryPoint 作为合约固有的低效率:每捆绑一次操作需要花费约 10 万 gas,而每次用户操作则需要花费数千 gas。
-
需要确保以太坊属性延续到账户抽象用户。
此外,ERC-4337 还扩展了两个功能:
-
Paymasters:允许一个账户代表另一个账户支付费用,打破了在验证阶段只能访问发送人账户本身的规则,引入了特殊处理方法,以允许付款人机制并确保其安全。
-
聚合器:支持签名聚合,如 BLS 聚合或基于 SNARK 的聚合。这对在 Rollup 上实现最高级别的数据效率是必需的。
现有的相关研究
-
BLSWallet 代码(使用聚合功能):https://github.com/getwax/bls-wallet
-
EIP-7562 (最先提出账户抽象):https://eips.ethereum.org/EIPS/eip-7562
-
EIP-7701(基于 EOF 的嵌入式账户抽象):https://eips.ethereum.org/EIPS/eip-7701
还有哪些工作要做,如何权衡?
剩下要解决的主要问题是如何将账户抽象完全引入协议。最近较受欢迎一种方案是 EIP-7701,旨在基于 EOF 实现账户抽象,即账户可以设置一个单独的代码段用于验证,如果该账户设置了该代码段,那么在该账户交易的验证步骤中就会执行该代码。

EIP-7701 帐户的 EOF 代码结构
这种方法的优点在于,它清楚地表明有两种等效的方法来查看本地账户抽象:
-
EIP-4337(但作为协议的一部分)
-
一种新型的 EOA,其中的签名算法是 EVM 代码执行
如果我们一开始就严格限制验证过程中可执行代码的复杂性(不允许访问外部状态,甚至一开始就把 gas 限制得太低,以至于无法用于抗量子或保护隐私的应用),那么这种方法的安全性就非常明显了:它只是把 ECDSA 验证换成了需要类似时间的 EVM 代码执行。然而,随着时间的推移,我们需要放宽这些限制,因为允许隐私保护应用在没有中继器的情况下工作以及量子抗性都是非常重要的。要做到这一点,我们确实需要找到方法,以更灵活的方式解决 DoS 风险,而不要求验证步骤变得极端简约。
主要的权衡似乎是在「尽快采纳一些较少人满意的方案」与「等待更长时间,也许会得到一个更理想的解决方案」间做出选择。理想的方案很可能是某种混合方案。一种混合方案是更快地纳入某些用例,留出更多时间来解决其他用例。而另一种方案是首先在 L2 上部署账户抽象版本。然而,这么做的挑战在于,要让 L2 团队愿意为采用某个提案而付出努力,他们就必须确信 L1 和/或其他 L2 会在稍后采用兼容的版本。
我们需要明确考虑的另一个应用是密钥存储账户,它可以在 L1 或专用 L2 上存储账户相关状态,也可以在 L1 和任何兼容的 L2 上使用。要高效做到这一点,可能需要 L2 支持L1SLOAD或REMOTESTATICCALL等操作码,也需要 L2 上的账户抽象实现作为支持。
对路线图的其他部分有何影响?
包含列表(Inclusion lists)需要支持账户抽象交易。在实践中,包含列表的需求和去中心化 mempool 的需求最终将非常相似,尽管前者的灵活性稍高一些。
此外,账户抽象的实现最好能在 L1 和 L2 上尽可能统一。如果将来我们预计大多数用户都会使用密钥存储 Rollup,那么在设计账户抽象时就应该考虑到这一点。
EIP-1559 改进
EIP-1559 旨在解决什么问题?
EIP-1559于 2021 年在以太坊上激活,并显著改善了平均区块包含时间。
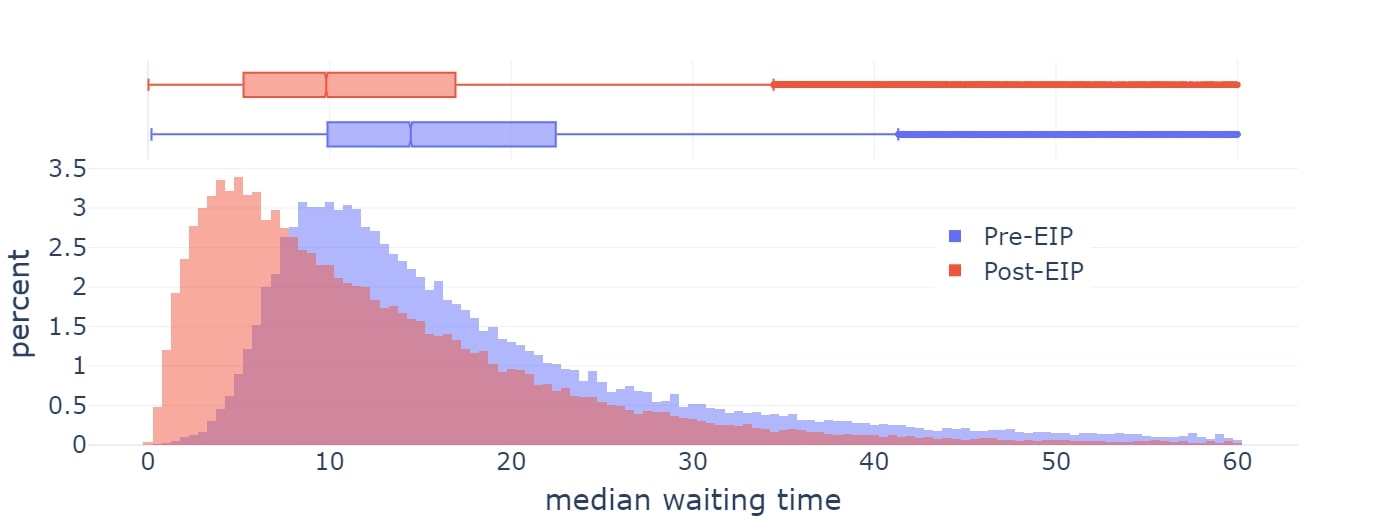
然而,目前 EIP-1559 的实施在以下几个方面存在缺陷:
后来用于 Blob 的方案(EIP-4844)就是为了解决第一个问题而明确设计的,而且整体上更加简洁。不过,EIP-1559 本身和 EIP-4844 都没有试图解决第二个问题。因此,目前的现状是两种不同机制的混淆状态,甚至随着时间的推移,两种机制有可能都需要改进。
除此之外,以太坊资源定价还有其他一些与 EIP-1559 无关的缺陷,但可以通过调整 EIP-1559 来解决。其中的一个主要问题是平均情况与最坏情况的差异,即以太坊的资源定价必须设置为能够处理最坏情况,即一个区块的全部 gas 消耗占用一个资源,但平均情况的使用量远小于此,从而导致效率低下。
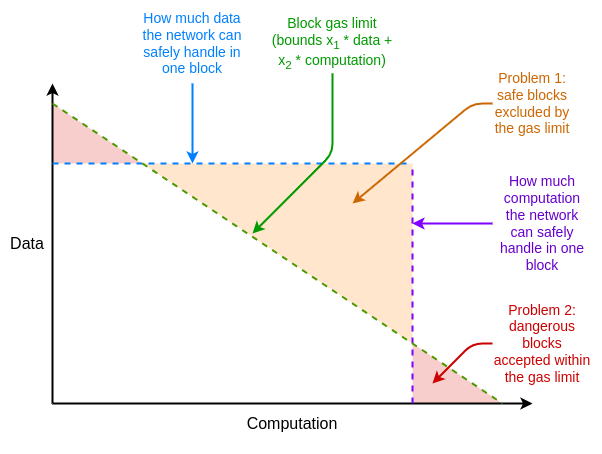
如何解决这些低效问题?
多维度 gas(multidimensional gas) 是解决这些低效问题的方法,可为不同的资源设定不同的价格和限制。这一概念在技术上独立于 EIP-1559,但 EIP-1559 使其变得更容易。如果没有 EIP-1559,如何优化打包一个具有多种资源限制的区块,将是一个复杂的多维度「knapsack」问题。有了 EIP-1559,大多数区块在任何资源上都不会满负荷运转,因此「接受任何支付足够费用的交易」这一简单算法就足够了。
如今,我们已在执行和 Blob 上设置了多维度 gas,而原则上,我们可以将其扩展到更多维度,包括 calldata、状态读/写和状态大小扩展。
EIP-7706为 calldata 引入了新的 gas 维度。同时,它也简化了多维度 gas 机制,使所有三种类型的 gas 都归属于一个(EIP-4844 风格的)框架,从而解决了 EIP-1559 的数学缺陷。
EIP-7623是解决平均情况与最坏情况资源问题的一个更彻底的方案,它在不引入全新维度的情况下,对最大 calldata 进行了更严格的限制。
另一个方向是解决更新率问题,找到一种更快的基费计算算法,同时保留 EIP-4844 机制引入的关键不变式(即从长远来看,平均使用量正好接近目标值)。
现有的相关研究
-
EIP-1559 常见问题:https://notes.ethereum.org/@vbuterin/eip-1559-faq
-
关于 EIP-1559 的经验分析:https://dl.acm.org/doi/10.1145/3548606.3559341
-
为实现快速调整而提出的改进建议:https://kclpure.kcl.ac.uk/ws/portalfiles/portal/180741021/Transaction_Fees_on_a_Honeymoon_Ethereums_EIP_1559_One_Month_Later.pdf
-
EIP-4844 常见问题,关于基费机制的部分: https://notes.ethereum.org/@vbuterin/protoo_danksharding_faq#How-does-the-exponential-EIP-1559-blob-fee-adjustment-mechanism-work
-
多维度 gas:https://vitalik.eth.limo/general/2024/05/09/multidim.html
还有哪些工作要做,如何权衡?
多维度 gas 主要有两个缺陷:
-
增加了协议的复杂性
-
增加了填满区块所需的最优算法的复杂性
对于 calldata 而言,协议复杂性是一个相对较小的问题,但对于「EVM 内部」的 gas 维度(如存储读写)而言,就成了一个较大的问题。难点在于,设置 gas 限制的不仅是用户,还有调用其他合约时设置限制的合约。而现在,它们设置限制的唯一方式是一维的。
解决这一问题的一个简单方法是,多维度 gas 只能在 EOF 内部使用,因为 EOF 不允许合约在调用其他合约时设置 gas 限制。非 EOF 合约在进行存储操作时,必须支付所有类型 gas 的费用(例如,如果SLOAD的费用是区块存储访问 gas 限额的 0.03%,那么非 EOF 用户也将被收取执行 gas 限额的 0.03%)。
对多维度 gas 的更多研究将有助于理解其中的利弊得失,并找出理想的平衡点。
对路线图的其他部分有何影响?
多维度 gas 的成功实施可以大大减少某些「最坏情况」下的资源使用,从而减轻为支持基于 STARK 的哈希二叉树而优化性能的压力。为状态大小的增长设定一个硬指标,将使客户端开发者更容易规划和预估未来的需求。
如上所述,由于 EOF 有着 gas 不可观测的特性,它能让更极端版本的多维度 gas 更容易实现。
可验证延迟函数(VDF)
VDF 旨在解决什么问题?
目前,以太坊使用基于 RANDAO 的随机性来选择提议者(proposer)。基于 RANDAO 的随机性的工作原理是要求每个提议者透露一个他们事先承诺的秘密,并将每个透露的秘密混合到随机性中。因此,每个提议者都有「1 位操纵权」,可以通过不出现来改变随机性(需要付出代价)。这对寻找提议者来说还算合理,因为放弃一个提议就能给自己带来两个新提议机会的情况非常罕见。但对于需要随机性的链上应用来说,这就不太合适了。理想的情况是,我们能找到一种更强大的随机性来源。
VDF 如何运作?
可验证延迟函数(VDF)是一种只能按顺序计算的函数,无法通过并行化提高速度。一个简单的例子就是重复哈希:计算for i in range(10**9): x = hash(x)。通过 SNARK 正确性证明,输出结果可用作随机值。我们的想法是,输入是根据 T 时可用的信息选择的,而输出在 T 时还不为人所知:只有在 T 时之后的某个时间,当有人完全运行计算时,才会知道输出。由于任何人都可以运行计算,因此不可能隐瞒结果,也就无法操纵结果。
可验证延迟函数的主要风险在于意外优化(unexpected optimization)。如果有人发现了如何以比预期快得多的速度运行函数,那么就可以根据未来的输出结果操纵他们在 T 时透露的信息。意外优化可能通过两种方式发生:
-
硬件加速:制造一种专用集成电路(ASIC),其运行计算循环的速度比现有硬件快得多。
-
意外的并行化:找到一种通过并行化更快地运行函数的方法,即使这样做需要多 100 倍的资源。
创建一个成功的 VDF 就要避免这两个问题,同时保持效率实用。(例如,基于哈希的方法的一个问题是实时的 SNARK 证明对硬件的要求很高。硬件加速通常通过让公共利益参与者自己为 VDF 创建和分发合理接近最优的 ASIC 来解决。)
现有的相关研究
-
vdfresearch.org:https://vdfresearch.org/
-
对以太坊使用的 VDF 攻击的思考,2018 年:https://ethresear.ch/t/verifiable-delay-functions-and-attacks/2365
-
针对 MinRoot(一种拟议的 VDF)的攻击:https://inria.hal.science/hal-04320126/file/minrootanalysis2023.pdf
还有哪些工作要做,如何权衡?
目前,还没有一种 VDF 结构能完全满足以太坊研究人员的要求。要找到这样一个函数,还有很多工作要做。而如果我们找到了完美的 VDF 结构,主要的权衡就在于功能与协议复杂性和安全风险。如果我们认为 VDF 是安全的,但它最终是不安全的,那么根据它的实现方式,安全性就会降低到 RANDAO 假设(每个攻击者只能操纵 1 位)或更差一些。因此,即使 VDF 出错也不会破坏协议,但会破坏应用或任何严重依赖 VDF 的新协议功能。
对路线图的其他部分有何影响?
VDF 是以太坊协议中一个相对独立的组成部分,除了提高提议者选择的安全性外,它还可用于依赖随机性的链上应用,以及加密的 mempool。不过,基于 VDF 的加密 mempool 仍依赖于额外的加密发现,而这些发现尚未出现。
需要牢记的一点是,鉴于硬件的不确定性,在生成 VDF 输出及该输出被纳入间会有一些「间隙」。这就意味着信息的获取需要提前几个区块。这可能是一个可以接受的代价,但在单个 slot 终结或委员会选择等设计中应加以考虑。
混淆和一次性签名(Obfuscation and one-shot signatures):密码学的遥远未来
我们要解决什么问题?
Nick Szabo 最著名的文章之一是 1997 年发表的一篇关于「上帝协议」的文章。在这篇文章中,他指出多方应用通常依赖于「可信第三方」来管理交互。在他看来,密码学的作用就是创建一个模拟的可信第三方来完成同样的工作,而实际上不需要信任任何具体的行为者。
「数学上值得信赖的协议」,由 Nick Szabo 绘制
到目前为止,我们只是部分接近这一理想。如果我们需要的只是一个透明的虚拟计算机(数据和计算无法被关闭、审查或篡改),隐私并非目标,那么区块链就可以做到这一点,尽管可扩展性有限。但如果隐私是目标之一,那么直到最近,我们还只能为特定应用制定一些特定协议,比如用于基本身份验证的数字签名、用于原始匿名形式的环形签名和可链接环形签名、基于身份的加密(以便在关于可信发行人的特定假设下实现更方便的加密)、用于Chaumian电子现金的盲签名等。这种方法需要为每个新应用付出大量努力。
2010 年代,我们首次看到了另一种基于可编程加密技术的更强大的方法。我们可以使用强大的新协议(特别是 ZK-SNARK)为任意程序添加加密保证,而不是为每个新应用创建一个新协议。ZK-SNARKs 允许用户证明他们所持有数据的任意声明,证明的方式易于验证,且除声明本身外不会泄露任何数据。这是在隐私和可扩展性方面同时迈出的一大步,在我看来,它就像是谷歌在人工智能领域中提出的 transformer。数千年来针对特定应用的难题突然有了一种通用的解决方案,而我们只需将其插入,就能解决各种令人烦心的问题。
而且,ZK-SNARKs 只是三个类似的极其强大的通用原语中的第一个。这些协议非常强大,每当我想到它们时,我就会想起童年《游戏王》中极其强大的埃及神卡组(强大到不允许在决斗中使用)。同样,在密码学中,我们也有「三神协议」:ZK-SNARKs、全同态加密(FHE)和混淆技术(Obfuscation)。
ZK-SNARKs、全同态加密和混淆技术如何运作?
我们已经将ZK-SNARKs 发展到了高度成熟的水平。在过去五年中,证明者速度和开发者友好性都有了很大提高,ZK-SNARKs 已成为以太坊可扩展性和隐私策略的基石。但是,ZK-SNARKs 有一个重要的限制,即需要知道数据才能对其进行证明。ZK-SNARK 应用中的每一个状态都必须有一个「所有者」,而这个 「所有者」必须能够批准对它的任何读取或写入。
第二种协议没有这种限制,它就是全同态加密(FHE)。FHE 允许在不看到数据的情况下对加密数据进行任何计算。这样,就可以为了用户的利益在用户数据上进行计算,同时保持数据和算法的私密性。它还可以扩展MACI 等投票系统,使其具有几乎完美的安全性和隐私保证。一直以来,FHE 饱受「实际应用效率太低」的诟病,但现在它已变得足够高效,出现了相关应用。
Cursive就是一个利用双方计算和 FHE 来发现共同利益并保护隐私的应用
但 FHE 也有其局限性,任何基于 FHE 的技术仍需有人持有密钥。秘钥持有的方式可以是 M-of-N 分布式设置,甚至可以使用 TEE 增加第二层防御,但仍是一个限制。
而这也引出了第三个协议,即不可区分混淆(indistinguishability obfuscation)。虽然该协议离成熟还很远,但到 2020 年,我们已经有了基于标准安全假设的理论上有效的协议,而且最近正在开始实施。不可区分混淆允许创建一个「加密程序」来执行任意计算,从而隐藏程序的所有内部细节。举个简单的例子,你可以把私人密钥放入一个经过混淆的程序中(该程序只允许你用它来签署质数),然后把程序分发给其他人。那么,这些人就可以使用该程序签署任何质数,但无法取出密钥。当然,不可区分混淆的功能远不止于此,与哈希算法一起,它可以用来实现任何其他加密原语,甚至更多。
经过混淆的程序唯一不能实现的就是防止自己被复制。但为此,将有更强大的功能即将出现,即量子一次性签名(quantum one-shot signatures),前提是人人都拥有量子计算机。
通过混淆和一次性签名,我们可以建立几乎完美的无信任第三方。我们唯一无法单独使用加密技术做到的事情,也是我们仍然需要区块链来实现的事情,就是保证抵御审查。这些技术不仅能让以太坊本身更加安全,还能在其基础上构建更强大的应用。
为了了解这些基元如何赋能,我们可以通过「投票」这个例子来进一步了解。投票是一个很有意思的话题,需要满足许多棘手的安全属性,包括非常强的可验证性和隐私性。虽然具有强大安全属性的投票协议已经存在了几十年,但如果我们需要一种可以处理任意投票协议的设计,比如二次投票、成对有界的二次融资(pairwise-bounded quadratic funding)、群组匹配二次融资(cluster-matching quadratic funding)等,那么我们希望「计票」步骤会是一个任意的程序:
-
首先,假设我们将投票公开放在区块链上。这样我们就有了公开可验证性(任何人都可以验证最终结果是否正确,包括计票规则和资格规则)和抗审查性(无法阻止人们投票),但没有隐私性。
-
其次,我们可以添加 ZK-SNARKs 保证隐私性:每张选票都是匿名的,同时确保只有获得授权的投票者才能投票,而且每个投票者只能投一次票。
-
然后,我们可以加入MACI 机制。投票会被加密为中央服务器的解密密钥。中央服务器需要执行计票过程,包括剔除重复投票,并发布 ZK-SNARK 证明答案。这就保留了之前的保证(即使服务器在作弊!),但如果服务器是诚实的,就可以增加抗胁迫保证(coercion-resistance guarantee):用户即使想证明自己是如何投票的,也无法证明。这是因为,虽然用户可以证明自己投了一票,但却无法证明自己没有投另一票来抵消这一票。这可以防止贿赂和其他攻击。
-
接着,我们可以在 FHE 内部进行统计,用 N/2 of N 的阈值解密计算对其进行解密,使得抗胁迫性保证为N/2-of-N,而不是 1-of-1。
-
随后,我们可以对统计程序进行混淆处理,并设计混淆程序,使其只有在获得许可的情况下才能输出结果,许可可以是区块链共识证明,也可以是一定数量的工作证明,或者两者兼而有之。这会使得抗胁迫保证几乎是完美的:在区块链共识的情况下,需要 51% 的验证者串通一气才能破解;而在工作证明的情况下,即使每个人都串通一气,用不同的投票者子集重新进行统计以试图提取单个投票者的行为的成本也是极其高昂的。我们甚至可以让程序对最终计票结果进行小幅随机调整,从而使提取单个投票者的行为变得更加困难。
-
最后,我们可以添加一次性签名(one-shot signatures,一种依赖于量子计算的基本原理,允许签名只能用于对特定类型的信息进行一次签名),使抗胁迫保证真正做到完美。
不可区分混淆还允许其他强大的应用。例如:
-
DAO、链上拍卖以及其他具有任意内部秘密状态的应用。
-
真正通用的可信设置:可以创建一个包含密钥的混淆程序,将
hash(key, program)作为程序的输入,并运行任何程序提供输出。有了这样一个程序,任何人都可以将其放入自己的程序中,将程序中预先存在的密钥与自己的密钥结合起来,从而扩展设置。这可以用来为任何协议生成 1-of-N 的可信设置。 -
仅通过单个签名进行验证的 ZK-SNARKs:实现这一点非常简单,在可信设置中,有人会创建一个混淆程序,只有当信息是有效的 ZK-SNARK 时,该程序才会用密钥签名。
-
加密 mempool:对交易进行加密,使其只有在未来发生链上事件时才会被解密。这甚至包括 VDF 的成功执行。
有了一次性签名,我们可以让区块链免受 51% 的最终性逆转攻击,尽管审查攻击仍然可能存在。与一次性签名类似的基元可以赋能量子货币(quantum money),无需区块链即可解决双重支出问题,不过许多更复杂的应用仍然需要区块链。
如果这些原语能够变得足够高效,那么世界上大多数应用都可以去中心化。主要的瓶颈在于验证实现的正确性。
现有的相关研究
-
不可区分混淆协议 2021 年: https://eprint.iacr.org/2021/1334.pdf
-
混淆协议如何帮助以太坊:https://ethresear.ch/t/how-obfuscation-can-help-ethereum/7380
-
首个已知的一次性签名构建:https://eprint.iacr.org/2020/107.pdf
-
混淆协议的尝试实施 (1):https://mediatum.ub.tum.de/doc/1246288/1246288.pdf
-
混淆协议的尝试性实现 (2): https://github.com/SoraSuegami/iOMaker/tree/main
还有哪些工作要做,如何权衡?
首先,不可区分混淆技术的发展极其不成熟, 候选结构的开发速度比应用慢上几百万倍,根本无法使用。不可区分性混淆以「理论上」多项式时间的运行时间而闻名,但实际运行时间比宇宙寿命还长。虽然,最新的协议已使运行时间不再那么极端,但对于常规使用来说,开销仍然太高。 此外,量子计算机甚至都不存在。我们目前在互联网上可能读到的所有构造,要么是原型机,不能进行任何大于 4 比特的计算,要么不是真正的量子计算机,因为它们虽然可能有量子部件,但不能运行真正有意义的计算,如肖尔算法或格罗弗算法。 最近,有迹象表明,「真正的」量子计算机已不再遥远. 然而,即使「真正的」量子计算机很快就会出现,普通人在笔记本电脑或手机上拥有量子计算机的那一天,很可能是在强大的机构获得能破解椭圆曲线密码学的量子计算机之后的几十年。 对于不可区分混淆,一个关键的权衡是安全假设。有一些更激进的设计使用奇特的假设。这些设计的运行时间通常更符合实际情况,但这些特殊假设最终可能会被打破。随着时间的推移,我们最终可能会对格密码有足够的了解,从而做出不会被打破的假设。然而,这条路风险更大。更保守的方法是坚持使用安全性可证明可还原为「标准」假设的协议,但这可能意味着我们需要更长的时间才能获得运行速度足够快的协议。
对路线图的其他部分有何影响?
功能极其强大的加密技术可以彻底改变游戏规则。举个例子:
-
如果我们能得到像签名一样容易验证的 ZK-SNARKs ,我们可能就不需要任何聚合协议了,我们可以直接验证链上的签名。
-
一次性签名可能意味着更安全的权益证明协议。
-
许多复杂的隐私协议都可以用「仅仅」拥有一个保护隐私的 EVM 来代替。
-
加密 mempool 更容易实现。
起初,应用层会受益匪浅,因为以太坊 L1 本身需要在安全假设上予以坚守。然而,仅应用层的使用就能改变游戏规则,就像 ZK-SNARKs 的出现一样。



















